原則として、 シェーダーに関する講義では、すでに法線マップを使用しましたが、グローバル座標系でのみ指定しました。 会話は接線空間についてです。 そのため、ここには2つのテクスチャがあり、左のテクスチャはグローバルスペースに設定され(RGBはXYZベクトルに直接変換されます)、右のテクスチャは接線です。

接線空間で指定された法線を使用するには、ピクセルを描画するために、接線フレーム(Darbouxフレーム)を計算します。 このフレームでは、1つのベクトル(z)が表面に直交し、他の2つは表面の接平面を定義します。 次に、テクスチャから法線ベクトルを読み取り、その座標を新しく計算されたフレームからグローバルフレームに変換します。 法線マップはほとんどの場合法線のわずかな摂動のみを定義するため、テクスチャの主要な色は青です。
なぜそのような困難なのでしょうか? 以前のように単純なグローバルベンチマークを使用しないのはなぜですか? モデルをアニメーション化したいと想像してください。 例えば、私は旧友のネグロを連れて口を開いた。 明らかに、修正されたサーフェスには他の法線が必要です!
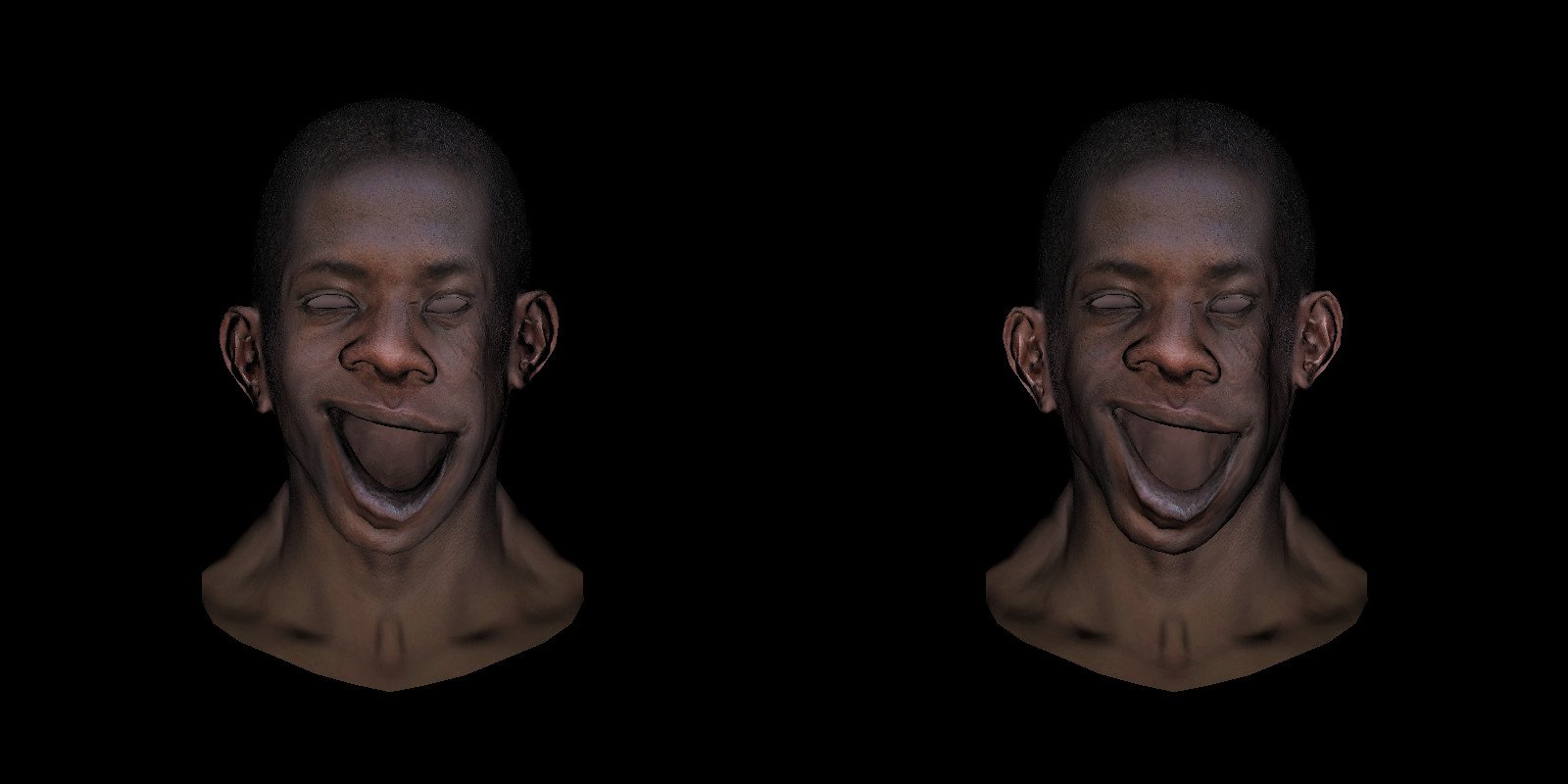
これが左側のモデルで、口が開いており、法線マップ(グローバル)は変更されていません。 下唇の粘膜を見てください。 口を閉じたモデルでは、光は顔に直接当たります。もちろん、粘膜はまったく照らされませんでした。 口は開きましたが、まだ点灯していませんでした...右の図は、接線空間で定義された法線マップを使用して計算されました。
したがって、アニメーションモデルがある場合、グローバル空間で法線マップを定義するには、アニメーションの各フレームに1つのテクスチャが必要です。 また、接線空間は自然にサーフェスに追従するため、必要なテクスチャは1つだけです!
次に2番目の例を示します。

これらは、ディアブロモデルのテクスチャです。 テクスチャには片手しか見えないことに注意してください。 そして、尾の半分だけ。 アーティストは、左手と右手に同じテクスチャーを使用し、尾の左右の部分に同じテクスチャーを使用しました。 (ところで、これがアンビエントオクルージョンの計算を妨げた理由です。)これは、グローバル座標系で、左手または右のいずれかに法線ベクトルを設定できることを意味します。 しかし、一度に2人ではありません!
それで、私たちはモチベーションで終わり、計算に直接行きます。
開始点、フォンシェーディング
それでは、 開始点を見てみましょう。 シェーダーは非常にシンプルで、フォンシェーディングです。
struct Shader : public IShader { mat<2,3,float> varying_uv; // triangle uv coordinates, written by the vertex shader, read by the fragment shader mat<3,3,float> varying_nrm; // normal per vertex to be interpolated by FS virtual Vec4f vertex(int iface, int nthvert) { varying_uv.set_col(nthvert, model->uv(iface, nthvert)); varying_nrm.set_col(nthvert, proj<3>((Projection*ModelView).invert_transpose()*embed<4>(model->normal(iface, nthvert), 0.f))); Vec4f gl_Vertex = Projection*ModelView*embed<4>(model->vert(iface, nthvert)); varying_tri.set_col(nthvert, gl_Vertex); return gl_Vertex; } virtual bool fragment(Vec3f bar, TGAColor &color) { Vec3f bn = (varying_nrm*bar).normalize(); Vec2f uv = varying_uv*bar; float diff = std::max(0.f, bn*light_dir); color = model->diffuse(uv)*diff; return false; } };
シェーダーの結果は次のとおりです。

トレーニングとデバッグを容易にするために、肌のテクスチャを削除し、赤と青の水平線で最も単純な通常のメッシュを適用します。

この写真の例でシェーダーFongがどのように機能するかを見てみましょう。
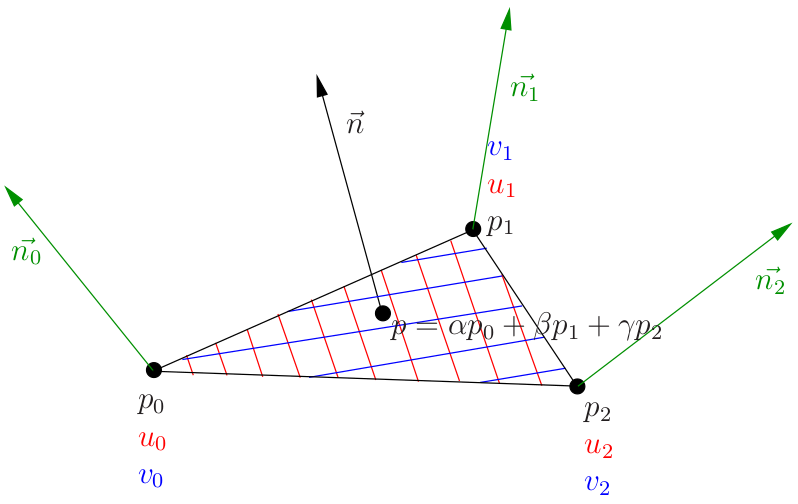
したがって、三角形の各頂点に対して、座標p、テクスチャ座標uv、および頂点nの法線ベクトルが与えられます。 各ピクセルを描画するために、ラスタライザーはピクセルの重心座標(アルファ、ベータ、ガンマ)を提供します。 これは、現在のピクセルの空間座標がp = alpha p0 + beta p1 + gamma p2であることを意味します。 テクスチャ座標をまったく同じ方法で補間してから、法線ベクトルも補間します。
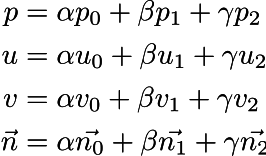
赤と青の線はそれぞれ等値線uとvであることに注意してください。 したがって、サーフェス上の各ポイントに対して、(スライドする)ダルブーフレームを設定します。このフレームでは、x軸は赤の線に、y軸は青に、zはサーフェスに直交します。 このベンチマークでは、法線ベクトルが定義されています。
3点で線形関数を計算します
したがって、私たちのタスクは、描画される各ピクセルのDarbouラッパーを定義するベクトルのトリプルを計算することです。 始めに、各点(x、y、z)に対応する空間で定義された線形関数fが実数f(x、y、z)= Ax + By + Cz + Dであることを想像してみましょう。数字(A、B、C、D)はわかりませんが、三角形(p0、p1、p2)の頂点の関数の値はわかります。
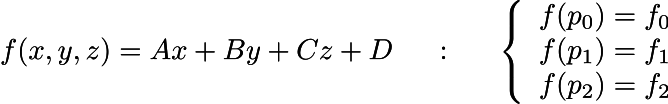
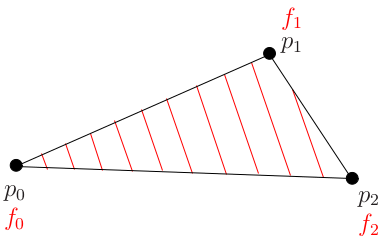
fは単に傾斜面の高さであると想像できます。 平面上の3つの異なる点を修正し、これらの点の高さを知っています。 三角形の赤い線は、高さの輪郭を示しています。高さf0、高さf0 + 1メートル、f0 + 2メートルなどの輪郭です。 線形関数の場合、これらすべての輪郭は明らかに平行な線です。
私たちが興味を持っているのは、等値線の方向ではなく、等値線の方向です。 特定の輪郭に沿って移動する場合、高さは変わりません(ありがとう、船長)、輪郭から方向を少しずらすと、高さが変化し始め、高さの単位あたりの最大の変化は方向に移動するときです輪郭に直交します。
関数の最も速い上昇の方向は、その勾配に他ならないことを思い出してください。 一次関数f(x、y、z)= Ax + By + Cz + Dの場合、その勾配は定数ベクトル(A、B、C)です。 平面上のどの点も等しく傾斜しているため、一定であることが論理的です。 数字(A、B、C)がわからないことを思い出してください。 3つの異なるポイントでのみ関数の値を知っています。 A、B、Cを復元できますか? もちろん。
したがって、3つのポイントp0、p1、p2と、関数f0、f1、f2の3つの値があります。 関数fの最速成長の方向を与えるベクトル(A、B、C)を見つけることに興味があります。 便宜上、g(p)= f(p)-f(p0)として定義される関数g(p)を考えます。
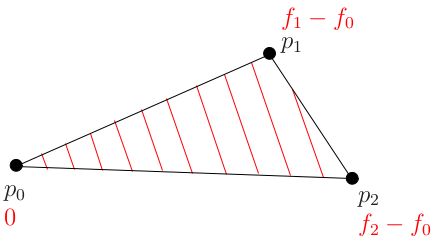
明らかに、傾斜を変更せずに傾斜面を移動しただけなので、関数gの最速成長の方向は、関数fの最速成長の方向と一致します。
g関数の定義を書き直しましょう:
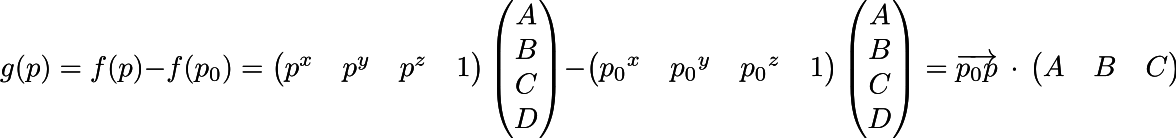
上付き文字p ^ xは、度ではなくpのx座標であることに注意してください。 つまり、関数gは、現在の点pを点p0に接続するベクトルとベクトル(A、B、C)のスカラー積です。 しかし、まだわかりません(A、B、C)! 怖くない、今すぐ見つけるよ。
それで、私たちは何を知っていますか? ポイントp0からp2に移動すると、関数gはf2-f0に等しくなることがわかっています。 つまり、ベクトルp2-p0とABCの間のスカラー積はf2-f0です。 ドット(p1-p0、ABC)= f1-f0についても同じことが言えます。 つまり、三角形の法線に同時に直交し、スカラー積に次の2つの制限があるベクトル(ABC)を探しています。
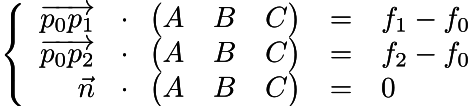
同じことを行列形式で書きます。
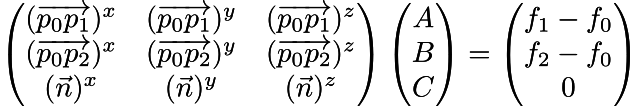
つまり、簡単に解くことができる行列方程式Ax = bが得られました。
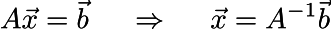
私は2つの意味で文字Aを使用したことに注意してください。意味は文脈から明らかになるはずです。 つまり、未知のベクトルx =(A、B、C)を乗算した3x3行列Aは、ベクトルb =(f1-f0、f2-f0、0)を与えます。 未知のベクトルは、Aの逆行列にベクトルbを乗算することで見つかります。
関数fに依存する行列Aには何もないことに注意してください! 三角形のジオメトリに関する情報のみが含まれます。
Darbouラッパーを計算し、法線マップを適用します(外乱)
合計で、Darbouxフレームはベクトル(i、j、n)のトリプルです。nは法線ベクトルで、iとjは次のように計算できます。
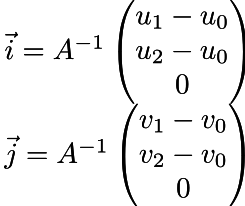
以下は、接線空間で定義された法線マップを使用する最終コードです。ここでは、 Phongティントと比較したコードの変更点を見つけることができます。
ここではすべてが非常に簡単です。マトリックスAを計算します。
mat<3,3,float> A; A[0] = ndc_tri.col(1) - ndc_tri.col(0); A[1] = ndc_tri.col(2) - ndc_tri.col(0); A[2] = bn;
次に、Darbouのラッパーベクトルを計算します。
mat<3,3,float> AI = A.invert(); Vec3f i = AI * Vec3f(varying_uv[0][1] - varying_uv[0][0], varying_uv[0][2] - varying_uv[0][0], 0); Vec3f j = AI * Vec3f(varying_uv[1][1] - varying_uv[1][0], varying_uv[1][2] - varying_uv[1][0], 0);
さて、それらを計算したら、テクスチャから法線を読み取り、ダーブフレームからグローバルフレームへの最も単純な座標変換を行います。
どちらかといえば、座標変換についてはすでに説明しました 。
これが最終レンダリングです。ディテールをフォンティントと比較してください:
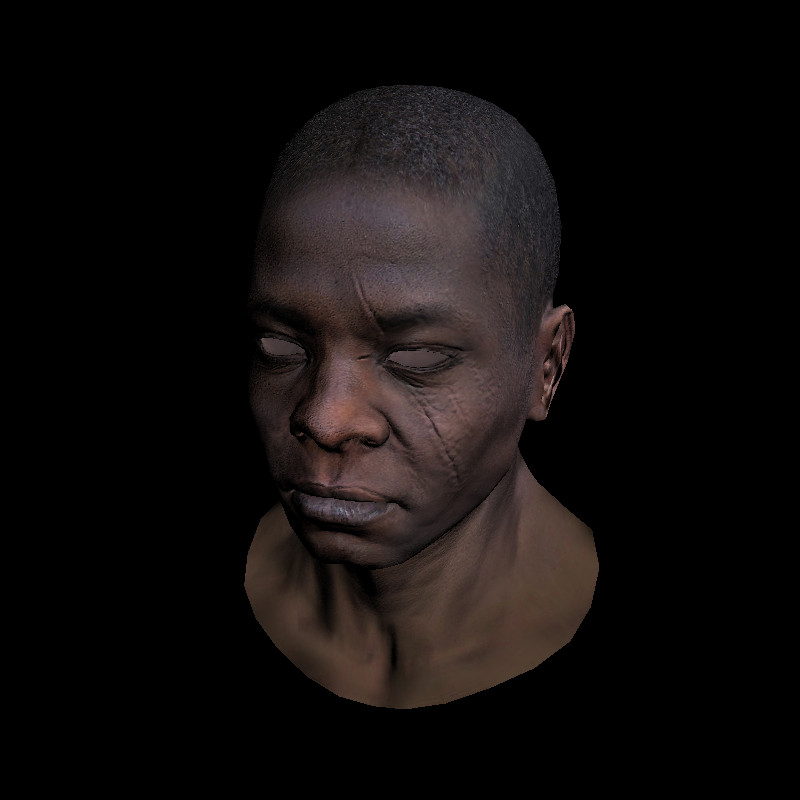
デバッグのヒント
線がどのように描かれるかを思い出してください 。 モデルに通常の赤青グリッドを課し、すべての頂点が結果のベクトル(i、j)を描画するため、それらはテクスチャの赤青線の方向とよく一致するはずです。
ハッピーコーディング!
あなたはどれだけ気配りがありましたか?
一般に、(平らな)三角形には法線ベクトルがあり、マトリックスAの最後の行で補間された法線を使用していることに気づきましたか? なぜこれをしたのですか?