どのごみをいつ知っていますか
恥を知らずに詩が成長する
この記事のトピックは、「Real-Time C ++」という本を読んでいる間、より具体的には、測定された分圧器の構造を調べた結果の結果が簡単に(シフト操作のみを使用して)スケーリングされるように、セクション6.13を読んでいるときに予期せず発生しました。 そのため、121ページのセクションの最後に、得られた値の誤差を推定するための式が示されていたため、混乱が生じました。 この本は「子どもたちに見える」と取り返しのつかない精神的トラウマを得るので、彼らが書かれたことに批判的でなければ、若いエンジニアによる測定誤差を推定する方法論の理解に特定の順序を導入する目的でこの投稿を作成しました。
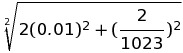
まず、要点を思い出して、用語を定義し、いくつかの重要な事実を確立しましょう。
測定値は常に、測定パラメーターの近似値を表し、正確な値からの測定値の偏差の程度を推定するために、誤差dX = | X-Xo |、dXは絶対誤差、Xは測定値、Xoは真の値です(どこかでそれを知っていると仮定されます)。
相対誤差qX = dX / Xo(同じ表記法)も非常に重要です。これは、得られる結果の精度が絶対値よりもはるかに優れていることを特徴としています(ただし、Xo = 0には特定の問題があります)。 それにもかかわらず、電子回路のコンポーネントのパラメータを、たとえば抵抗器-5%または1%などの精度の形で示すために、相対誤差がよく使用されます。
コンポーネントの公称値の期待値からの偏差の最大値のみが与えられ、この偏差の分布法則に関する仮定はなく、線形分布、三角形、および尾部が切り取られたガウス分布、したがって、標準偏差は作成せず、将来的には最大偏差のみで動作します。 このアプローチは私たちの場合により適切です(私たちはトレーナーではなくエンジニアです)、あなたの顧客が98%のケースで動作する回路に満足する可能性は低いです、私たちが設計した回路は常に動作します(もちろん許容可能な動作条件内で)。
測定されたパラメーターまたはコンポーネントパラメーター値が純粋な形で使用されることはほとんどなく、ほとんどの場合、それらは他のパラメーターまたは定数とともにさまざまな伝達関数の一部であるため、この種のさまざまな式の精度特性を計算するためのルールが必要です。 最大誤差のみを推定することをもう一度強調します。
最も単純な関数f(X)= K * X(スケーリング関数)から始め、メンバーの精度に応じて、この関数の結果の精度を取得します。 定数Kが絶対に正確に与えられると仮定して、直接計算の最も単純な方法qf(X)= | f(X)-f(Xo)| / f(Xo)、これにより式q(k * X)= | K *(Xo + dX)-K * Xo | /(K * Xo)、またはq(K * X)= | K * dX | /(K * Xo)= dX / Xo、したがってq(K * X)= qX。これは、スケーリング時に相対誤差が変化しないことを意味します。
次に重要な関数は、逆値f(X)= 1 / Xを取得することです。
q(1 / X)= | 1 /(Xo + dX)-1 / Xo | /(1 / Xo)、変換後
q(1 / X)= | -dX /((Xo + dX)* Xo)| * Xo = | -dX /(Xo + dx)|、
dX << Xoと仮定すると、q(1 / X)〜dX / Xo = qXが得られます。つまり、逆の値をとると、相対誤差は変化しません。
ここで、合計関数f(X、Y)= X + Yを考えます。同様の計算を実行して、
q(X + Y)= | ((Xo + dX)+(Yo + dY))-(Xo + Yo)| /(Xo + Yo)= | dX + dY | /(Xo + Yo)= qX * Xo /(Xo + Yo)+ qY * Yo /(Xo + Yo)。 2つの数量を加算すると、絶対誤差が加算され、相対誤差は正確な値の値に従ってスケーリングされると確信しました。
両方の量の相対誤差が一致する場合、q(X + Y)= qX *(Xo + Yo)/(Xo + Yo)= qX = qYになります。つまり、同じ相対誤差で2つの値を加算すると、合計の相対誤差同じになります。
得られた結果から興味深い結論が得られます。抵抗回路の等価抵抗の相対精度は、コンポーネントの相対精度に等しく、定格や接続図には依存しません。 実際、直列接続では抵抗が加算され、加算中に維持される精度を設定します。接続が並列の場合、導電率(抵抗に反する値)が加算され、逆を取る場合に維持される精度も設定します。 その結果(少なくとも私にとって)はやや予想外ですが、判明しました。
さらに検討するために、2つの量の乗算関数の精度も必要です。同様に取得します
q(X * Y)= | (Xo + dX)*(Yo + dY)-Xo * Yo | /(Xo * Yo)= | dX * Yo + dY * Xo + dX * dY | /(Xo * Yo)=
= dX / Xo + dY / Yo + dX / Xo * dY / Yo = qX + qY + qX * qY、qY〜qY << 1を考慮して、最終的にq(X * Y)= qX + qY、つまり乗算するとき相対誤差が加算されます。
除算を逆値による乗算と見なし、この結果を除算q(X / Y)= qX + qYに拡張します。
これで、抵抗分割器の透過係数の精度を計算する準備ができました。これは、式によって決定されます
K(R、r)= r /(R + r)。 まず、式を部分的に検討し、qr = rを仮定して、qK(R、r)= qr + q(R + r)= qr + qR * R /(R + r)+ qr * r /(R + r)を推定しますqR、qK(R、r)= 2 * qRを取得します。
ポストの冒頭で示された本で使用されたのはそのような結果でしたが、関数の分数の分子と分母は独立していると信じていたので、それは完全に真実ではありません。
相対誤差を得るための試行されたテスト方法に頼って結果を改良し、取得します(中間計算は好奇心reader盛な読者に任せますので、式の不便な記述のために恐らく私をoldります。 r)=(qR + qr)* R /(R + r)。
したがって、洗練された誤差式は、除算器の伝達係数の精度がqK(R、r)= 2 * qR *(1-K)の形式で除算係数K = r /(R + r)に依存することを示していることがわかります。非常に小さな伝送係数(K << 1)についてのみ誤差が2倍になります。たとえば、1/2の分割係数では、係数の相対誤差は抵抗の相対誤差と一致しますが、これもやや予想外です。 本で指定された公称値の場合、エラーは2 * 64.9 /(11.8 + 64.9)= 1.7 * qRになりますが、これは最初の結果(2 * qR)に近いものの、それでもまだ遠くなります。
さて、最後の発言-最大偏差を推定することを繰り返し強調したため、平均二乗値の計算は決して歓迎できず、ADCの出力のコードは式N = Uin * Katspで記述されているので、これらの値の相対誤差を追加するだけでqNが得られます= qUin + qKacp = 1.7 * 0.01 + 2/1024〜1.9%<2%。ただし、これは本に示されている結果に対応しています。
もう1つの重要な状況を考慮する必要があります-伝送係数の誤差が入力電圧に依存しない場合、ADCの誤差について言うことはできません-入力電圧に関係なく2 EMPになります(実際、すべてがはるかに複雑ですが、簡単にするために受け入れました)、得られた相対測定誤差は、最大に近い応力に対してのみ有効であり、他の場合には増加します。