
この記事を書く理由は2つあります。 1つ目は、テストでグラフカバレッジのタイプをどのように使用できるかを示し、状態と遷移のテスト手法の実用的な別の例を示します。 第二に-反論することはできませんが、少なくともテスターは数学
ネットワークには、インストーラーのテストプロセスとその作業の結果を説明する資料が非常に多くあります。 このテーマには多くのチェックリストとその他の利点があります。 以下では、インストールプロセスのかなり狭い部分、つまりウィザード自体のテストについて説明します。 ウィザードのすべての画面を調べて、うまく機能していると主張するだけで十分ですか? 「戻る」、「次へ」、「キャンセル」の各ボタンを1回クリックするだけで十分でしょうか? 無限のシナリオの数を制限する方法([戻る]ボタンと[次へ]ボタンを使用して、2つの隣接するインストーラー画面間を何度でも移動できます)。
説明のために、Windows用のLibreOffice 5インストーラーが使用されます。 それを選択する決定は、 詳細なステップバイステップのスクリーンショットが利用可能であるためです。 この記事では、グラフカバレッジに関する最初の記事と2番目の記事の表記を使用しています。
状態と遷移のグラフを作成する
最初に行うことは、状態を分離することです。 それは非常に簡単です:少なくとも、インストーラーのすべてのステップを状態として取る必要があります。 しかし、一般的に言えば、これはウィザードをチェックするのに十分ではありません。 ほとんどすべてのステップで、いくつかの変更を行うことができます。これにより、可能であれば、各画面に追加の状態が生成されます。 変更を行うことは重要です。前の画面に戻るときは、それらを保存する必要があるためです。
変更を保存する必要性も、移行時に考慮する必要があります。 元に戻すのではなく、変更した状態に戻す必要があります。 グラフを作成するとき、元の画面と変更された画面が同じであるという意味で、変更のないスクリプトが変更のあるスクリプトに含まれていることを考慮します。 したがって、インストーラーの内部画面に設定される標準の遷移は次のようになります。
戻る
|
画面->変更された画面->進む
さらに、最終状態を強調表示する必要があります。 ウィザードには2つあります。インストールがキャンセルされ、インストールが完了します。 簡単にするために、グラフではインストールプロセスの緊急中断を考慮していません。
ウィザードには次のような画面があります。
「ようこそ」のステータスに対応
「セットアップタイプ」状態に対応
「カスタム」のステータスに対応
カスタム変更に対応
「ファイルタイプ」および「ファイルタイプ変更」状態に対応
「インストール準備完了」および「インストール準備完了」の変更済み状態に対応
インストールインストールの進行状況に対応
インストール完了に対応
その結果、下のグラフが表示されました(スクリーンショットとの比較を容易にするために、英語のボタン名とインストーラー画面の短い名前が使用されました)。 矢印の上にそのようなマークがあります:
- キャンセル-キャンセル
- 次-次
- 戻る-戻る
- 変更-元の画面から変更を加えます。
標準およびカスタム-2番目の画面でオプションを選択します。 変更された状態名の一部は、画面に変更が加えられたことを示します。 「変更」遷移の結果として、このマークのない同じ状態からのみ、変更済みとマークされた状態に到達できます。
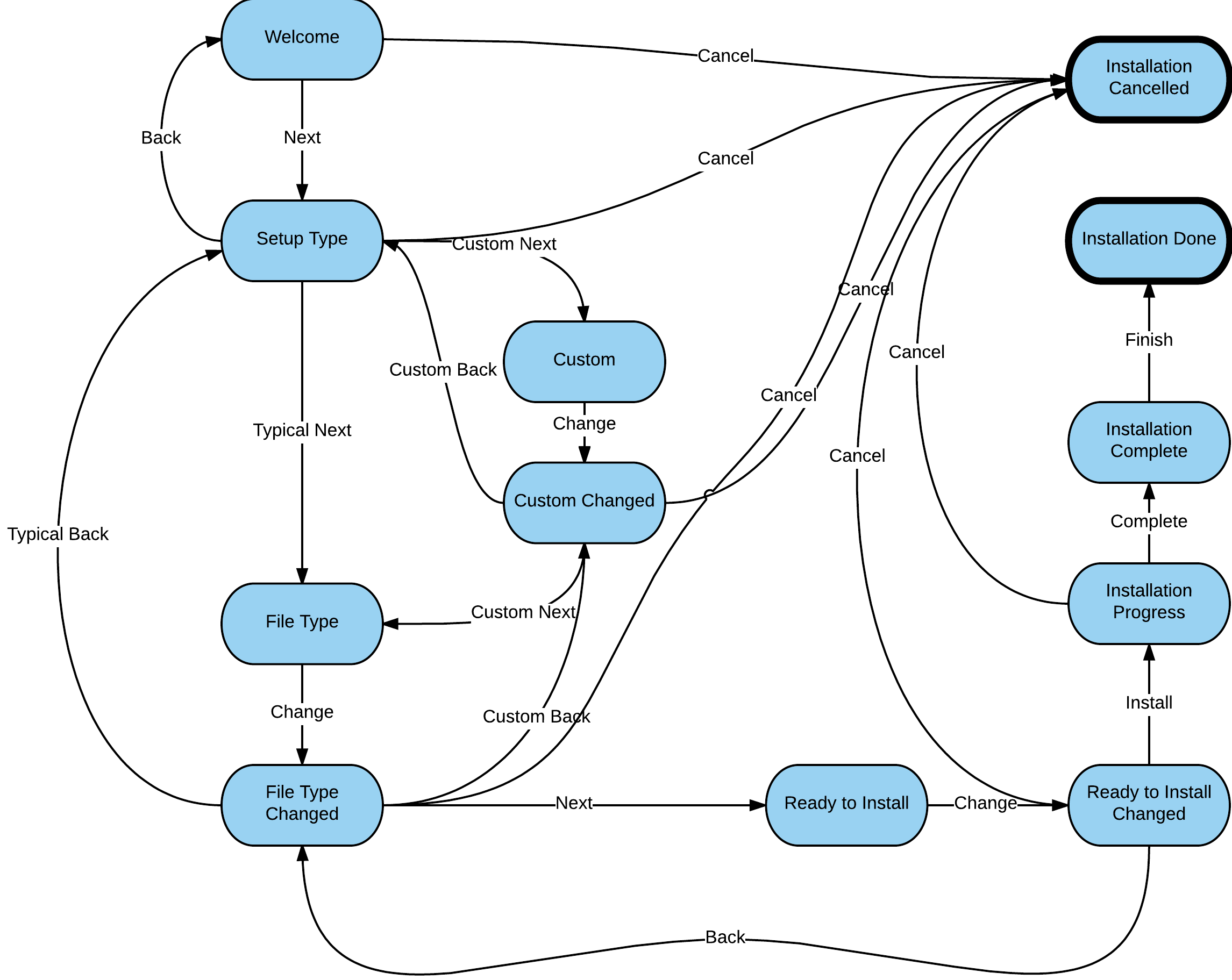
インストーラーの状態と遷移グラフ
かなり面倒でしたが、解読できるといいのですが。
カバレッジの種類とテストスイート
次に、さまざまなタイプのグラフカバレッジを扱い、それらに対応する十分なテストセットをコンパイルします。 これを行うために、参照しやすくするために状態に番号を付け直します(グラフの範囲に関する最初の記事と2番目の記事で行われたように)。 各タイプのカバレッジで要件とテストを指定する構文は、同じ場所から取得されます。
1-ようこそ
2-セットアップの種類
3-カスタム
4-カスタム変更
5-ファイルの種類
6-ファイルタイプの変更
7-インストールの準備ができました
8-インストール準備完了の変更
9-インストールの進行状況
10-インストール完了
11-インストール完了(最終状態)
12-インストールがキャンセルされました(最終状態)
頂点カバレッジ
要件= {1、2、3、4、5、6、7、8、9、10、11、12}
パス(T)= {[1、12]、[1、2、3、4、5、6、7、7、8、9、10、11]}
このコーティングは実装が非常に簡単です。 十分と考えることができますが、これらのテストでは、サイクルが形成されるために以前の状態に戻るエッジは考慮されません。 このグラフの循環的複雑度を計算できます。
CA =#エッジ-#頂点+ 2 = 22-12 + 2 = 12
カバーエッジと指定されたパス
要件= {(1、12)、(1、2)、(2、1)、(2、12)、(2、3)、(2、5)、(3、4)、(4、12) 、(4、2)、(4、5)、(5、6)、(6、2)、(6、4)、(6、12)、(6、7)、(7、8)、( 8、6)、(8、12)、(8、9)、(9、12)、(9、10)、(10、11)}
パス(T)= {[1、12]、[1、2、12]、[1、2、3、4、12]、[1、2、5、6、12]、[1、2、5] 、6、7、8、12]、[1、2、5、6、7、8、9、12]、[1、2、1、2、5、6、2、3、4、2、3 、4、5、6、4、5、6、7、8、6、7、8、9、10、11]}
最後の最長のパスでは、すべての変更とすべての逆方向の遷移が考慮されます。 したがって、このパスは、閉じたパスを簡単にカバーします(各サイクルに1つのパス)。
他の種類のカバレッジを提供する価値があるかどうかは、インストーラーの手順の数、必要なシナリオを手動で設計するのにかかる時間、または特定のカバレッジの準備を自動化するのに必要な時間、品質のレベルによって異なります。 私の意見では、このインストーラー(および他のインストーラー)では、上記のテストと選択した種類のカバレッジの両方で十分です。