👩‍❤️‍👩 😴 👴🏻 ランダムシーケンスの品質をチェックするパッケージはどのように配置されますか？ 🖐️ 🚚 💈

ランダムおよび疑似ランダムシーケンスを取得する問題は、常に活発な関心を引き起こします[ 1 ] [ 2 ] [ 3 ] [など]。 NIST、DieHard、TestU01などの[ 1 ]、[ 2 ] [など]統計テストパッケージもしばしば言及されます。

Habrahabrに関する記事へのコメントには、これらのパッケージが最終的な数字をどのように取得するかについての質問があります。一般的に、複雑なことはありません-それは単なる統計です。読者がこれらの数字を取得する魔法に興味がある場合は、カットをお願いします。多くのブナや数式があります。

できれば、準備ができていないユーザーのためにプレゼンテーションをできる限り明確にしたいので、不正確な部分や省略された定義はご容赦ください。

一般的なスキーム

統計的シーケンス分析は、原則として2段階で行われます。

最初の段階は準備段階と呼ばれますが、これは最も時間がかかり、計算の大部分がここで実行されます。

1.1。調査したジェネレータを使用して、ランダムシーケンスが形成されます。

1.2。各シーケンスについて、テスト統計が計算されます。一連のテストが機能する場合（複数のテストが一度に実行される場合）、各テストについてシーケンスの統計が計算されます。

1.3。各シーケンスについて、有意確率が計算されます。

1.4。受信した統計と有意確率は保存されます。
第2段階では、結果の処理が実行されます。

2.1。受け入れ基準を使用して、統計の分布と仮説の分布に対する有意性の確率の対応に関する仮説がテストされます。

2.2。テストに合格したシーケンスの数が決定されます。最後の値の信頼区間が構築されます。

2.3。テストに合格したかどうかが決定されます。

2.4。最終的な結論。

概略的に、このプロセスは次のように表すことができます。

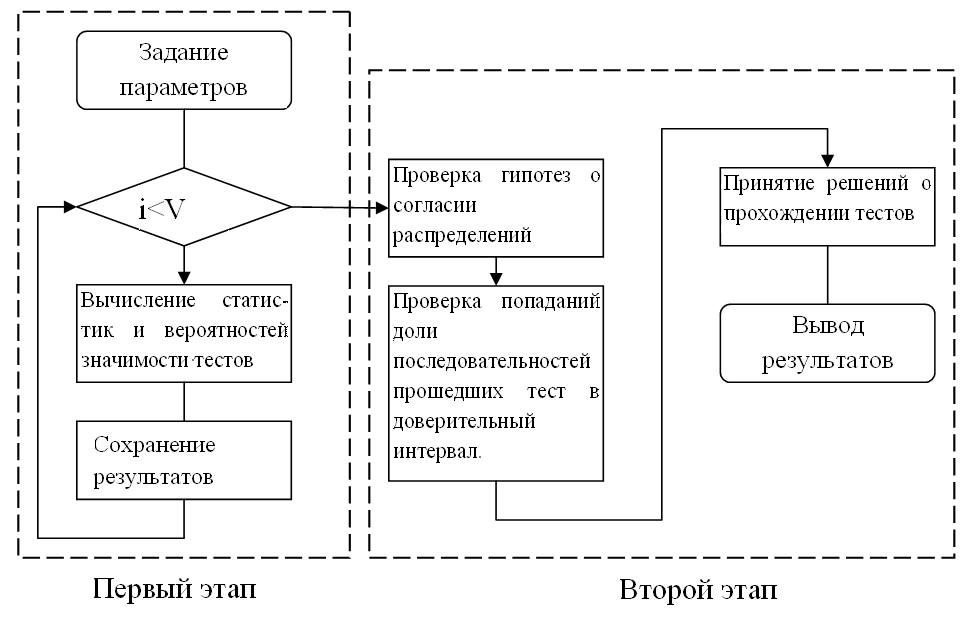
統計生成

各テストの目的は、テストシーケンスの分布が均一であるという仮説をテストすることです。より厳密に言えば、各記号 $\ varepsilon_i$ ランダムシーケンス $X = \ {{{\ varepsilon} _ {1}}、{{\ varepsilon} _ {2}}、\ ldots、{{\ varepsilon} _ {n}} \}$ 一様な確率分布が必要です： $P（\ varepsilon = x）= 1/2、x \ in \ {0,1 \}$ 。この仮説は $H_0$ （彼らは帰無仮説を言う）。

そして、テスト統計の公式はどこから来たのですか？ NISTパッケージの周波数テストの例を見てみましょう。

各統計的検定は、仮説を満足するランダムシーケンスが持つべき特定のプロパティに関する何らかの仮定をチェックします。 $H_0$ 。

NISTテストスイートの周波数テストの場合、この仮定は次のステートメントです。「シーケンスが仮説を満たしている場合 $H_0$ 、このシーケンスのゼロと1の数はほぼ同じである必要があります。

調査中のシーケンスの文字の合計が見つかった場合、最終結果はランダム変数になります。これを呼び出しましょう $\ゼータ$ ： $\ zeta = \ sum \ limits_ {i = 1} ^ {n} {{{{\ varepsilon} _ {i}}}$ 。中心極限定理によると、ランダム変数 $\ゼータ$ 私たちの仮定では、数学的な期待値で正規分布に近い分布を持つべきです $m = M \ゼータ= n / 2$ および標準偏差 $\ sigma = \ sqrt {D \ zeta} = \ sqrt {n} / 2$ 。

数学的期待値からのユニット数（ゼロ）の偏差に関心があるため、ランダム変数を検討します。 $\ゼータ-m$ 。に分割する $\ sigma = \ sqrt {D \ zeta} = \ sqrt {n} / 2$ 取得した値の分散が1に等しくなるようにします。また、偏差の符号は関係ないため、このモジュロをすべて使用します。どうしたの？

$S = \ frac {\左| \ zeta -m \ right |} {\ sigma} = \ frac {\ left | \ sum \ limits_ {i = 1} ^ {n} {{{\ varepsilon} _ {i}}}-n / 2 \ right |} {\ sqrt {n} / 2} = \ frac {\ left | 2 \ sum \ limits_ {i = 1} ^ {n} {{{\ varepsilon} _ {i}}}-n \ right |} {\ sqrt {n}}$ 。

研究中のシーケンスに応じて、ランダム変数が取得されました。仮説の下でのこの確率変数の分布関数 $H_0$ 等しい：

$F（x）= P（S \ le x）= 2 \ Phi（x）-1、x＆gt; 0$ （残りのxはゼロ）、

どこで $\ファイ（x）$ 標準正規分布の関数です。

特定のシーケンスXから計算された値Sは、「統計」と呼ばれます。 NISTテストの説明を見ると、テスト統計を計算するためのこの公式を正確に見つけることができます。

同様の考慮事項を使用して、他のテストの式が表示されます。

「良い」シーケンスと「悪い」シーケンスを区別する方法は？

統計Sがゼロから大幅に逸脱しているかどうかを判断する必要があります。

偏差は「大きすぎる」べきではありません。「あまりにも」という言葉は、行動のための具体的な指示を提供するものではありません。したがって、いくつかの重要なレベルを選択します $\アルファ$ -仮説を誤って拒否する確率 $H_0$ 。これに $\アルファ$ 臨界値に対応 ${{S} _ {\ alpha}}$ クリティカルエリアを定義します。これを写真で示しましょう。

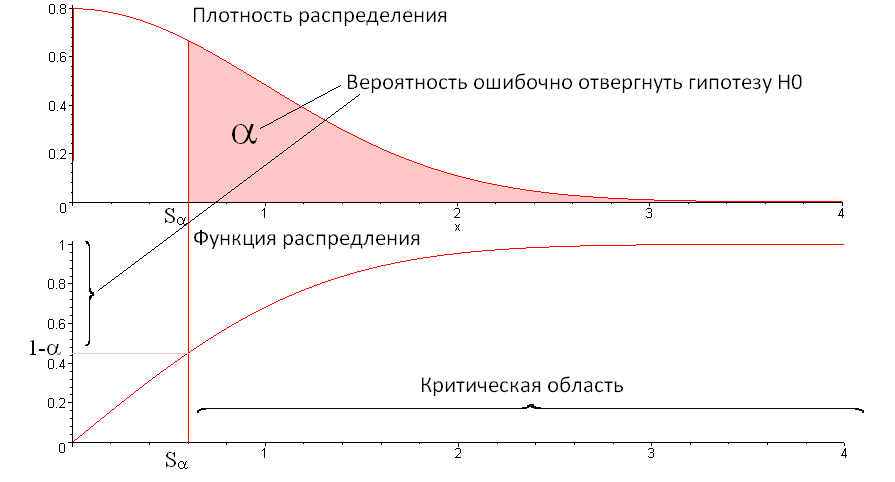
言い換えれば ${{S} _ {\ alpha}}$ シーケンスがテストに合格したかどうかを判断するための境界を表します。値が $S＆lt; {{S} _ {\ alpha}}$ 、その後、我々はシーケンスが「良い」と信じています-テストに合格しました。 Sがクリティカル領域にある場合 $S \ ge {{S} _ {\ alpha}}$ 、その後、シーケンスが悪いと見なします-テストは失敗しました。

統計調査パッケージでは、多くの場合、同等の別の意思決定方法が使用されます。統計Sに従って、確率確率pが計算されます。 $p = 1-F（S）$ 。この値は以下になります $\アルファ$ 、Sがクリティカル領域に該当する場合のみ。

通常 $\アルファ$ 0.01から0.001の範囲で選択されます。以上 $\アルファ$ 、より多くのシーケンスが拒否されます。

さらなる調査結果

すぐに問題が発生します：「シーケンスの一部が不良で一部が良好である場合に（疑似）乱数のジェネレーターを拒否する方法は？」

実際、ランダムシーケンスジェネレーターは常に、テストに失敗したシーケンスの一部を生成します。すべてのシーケンスがテストに合格した場合、これは非常に疑わしいとさえ言えます。

したがって、結果を処理します。

最初の段階で、長さnのVシーケンスが生成されます- ${{X} _ {1}}、{{X} _ {2}}、\ ldots、{{X} _ {V}}$ 。各シーケンスについて $X_i$ 統計が計算されます $S_i$ および有意性の確率 $p_i$ 、つまり 2つのセットが取得されます：統計セット $S_1、S_2、\ ldots、S_V$ および確率確率のセット ${{p} _ {1}}、{{p} _ {2}}、\ ldots、{{p} _ {V}}$ 。

第2段階では、取得したサンプルの処理が実行されます。 $S_1、S_2、\ ldots、S_V$ そして ${{p} _ {1}}、{{p} _ {2}}、\ ldots、{{p} _ {V}}$ 。

まず、同意基準がこれらのシーケンスに適用されます。サンプリング $S_1、S_2、\ ldots、S_V$ 上記の分布とサンプルが必要です ${{p} _ {1}}、{{p} _ {2}}、\ ldots、{{p} _ {V}}$ セグメント[0; 1]に均一な分布が必要です。たとえば、通常、最初のシーケンスにはKosmogorov-Smironov基準を適用し、2番目のシーケンスにはピアソン基準を適用します。

一般に、これらの基準の適用は、上記の統計的検定に似ています。違いは、適用された統計のみです。

ピアソン基準の適用

のために $P = \ {{{p} _ {1}}、{{p} _ {2}}、\ ldots、{{p} _ {V}} \}$ ピアソンの基準は次のように適用されます。

Pの可能な値の範囲（セグメント[0,1]）は、T個の同一のセグメントに分割されます。 Tの値は、通常、10や20など、それほど大きくないものを選択します。Pが均一な分布を持っていると仮定すると、平均でV / T値は各間隔に分類されます（ちなみに、TはV / T> 5になるように選択する必要があります）。

サンプルPからヒストグラムが作成されます $\ {F_0、F_1、\ ldots、F_ {T-1} \}$ -各間隔に入る値の数。次に、ピアソン統計が計算されます。 ${{\ chi} ^ {2}} = \ sum \ limits_ {i = 0} ^ {T-1} {\ frac {{{（{{{F} _ {i}}-V / T）} ^ { 2}}} {V / T}}$ 。これらの統計は、元のシーケンスが区間[0,1]に均等に分布しているという仮定の下で、自由度T-1のカイ2乗分布を持つ必要があります（let $F {T-1}（x）$ -T-1自由度のカイ二乗分布関数）。関数値 $F {T-1}（x）$ プログラムによって、または特別な表に従って（基準を手動で適用して）計算されます。

統計用 ${{\ chi} ^ {2}}$ 有意確率が計算されます $p = 1-{{F} _ {T-1}}（{{\ chi} ^ {2}}）$ 。もし

$p＆gt; \アルファ$ 、その後、均一分布仮説は拒否されません。

テストに合格するシーケンスはいくつですか？

次に、テストに合格したシーケンスの数が調べられます。

有意確率は区間[0,1]に均等に分布しているため、平均検定は合格するはずです $V（1- \アルファ）$ シーケンス。しかし、結果の数を比較します $V（1- \アルファ）$ 意味がありません。代わりに、信頼区間が構築されます。

テストに合格したシーケンスの一部の信頼区間を指定します。

シーケンス $\ {{{{p} _ {1}}、{{p} _ {2}}、...、{{p} _ {V}} \}$ 一貫したvベルヌーイ独立テストシーケンス $\ {{{{\ xi} _ {1}}、{{\ xi} _ {2}}、...、{{\ xi} _ {V}} \}$ ：

${{\ xi} _ {i}} = {{p} _ {i}}の場合1 \ ge \ alpha$

${{\ xi} _ {i}} = 0、{{p} _ {i}}＆lt; \ alpha。$

中心極限定理によると、ベルヌーイテストシーケンスの成功数の分布は、テストに合格したシーケンスの数と一致し、数学的な期待値で正常と見なすことができます。 $V（1- \アルファ）$ および分散 $V（1- \アルファ）\アルファ$ 。

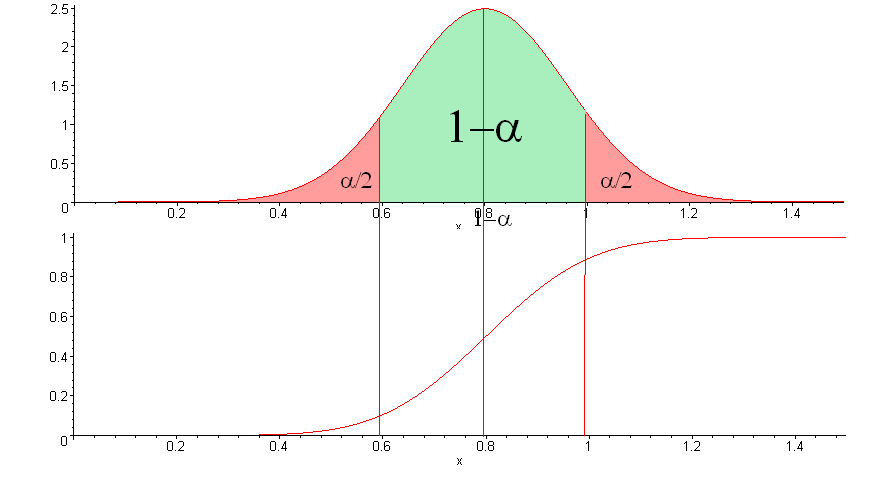
信頼のレベルを選択した場合 $（1- \アルファ）$ 、信頼区間は次のとおりです。

$\左（（1- \ alpha）+ {{\ Phi} ^ {-1}}（\ alpha / 2）\ sqrt {\ frac {（1- \ alpha）\ alpha} {V}};（1- \ alpha）-{{\ Phi} ^ {-1}}（\ alpha / 2）\ sqrt {\ frac {（1- \ alpha）\ alpha} {V}} \右）$

図では、信頼区間は緑の領域の下のx値です。

初期シーケンスが均一な分布を持っているという仮定の下で、確率でテストに合格したシーケンスの割合 $（1- \アルファ）$ この間隔に収まるはずです。

「ルール」を使用する場合 $3 \シグマ$ "、その後、間隔は次のようになります。

$\左（（1- \ alpha）-3 \ sqrt {\ frac {（1- \ alpha）\ alpha} {V}};（1- \ alpha）+3 \ sqrt {\ frac {（1- \ alpha ）\ alpha} {V}} \右）$

シーケンスの計算された割合が信頼区間内にある場合、テストは合格とみなされます。

テストバッテリーはどのように機能しますか？

上記は、1つのテストのテストの説明です。バッテリーに複数のテストが含まれている場合、説明されている調査は各テストに対して実行されます。

出力には、テストに合格したタブレットと合格したテストの割合が表示されます。

文学

NIST（暗号化アプリケーションのランダムおよび擬似乱数ジェネレーターの統計テストスイート）、 http：//csrc.nist.gov
Ivchenko G.I.、Medvedev Yu.I. 数学統計：教科書。高専のための手当。 -M。：より高い。 1984年。
Knut D.プログラミングの技術：3t。 -M。：ミール、1992
Van der Varden B.L.、数学統計。 -M。：外国文学の出版社、1960

ランダムシーケンスの品質をチェックするパッケージはどのように配置されますか？