ただし、アプリケーションでは、乱数と擬似乱数のシーケンスとともに、 均一な分布を持つ数の順列を取得する必要があります。 たとえば、暗号アプリケーションでは、このような置換の必要性が定期的に現れます。
以下に説明する方法は、1962年に[1]でSandelius(M. Sandelius)によって提案されました。
説明されているアルゴリズムにより、 均一な分布を持つn個の要素のランダムな順列を取得できます。 後者は、n!のいずれかを取得する確率を意味します。 この方法を使用して可能な置換は1 / n!..
順列アルゴリズム
サンデリウスの方法は、再帰的に記述する方が簡単です。
各ステップで、配列Pが処理されます。配列Pの場合、配列Pの要素数に等しい量のランダムビットが生成されます。シーケンスのi番目のビットは、配列Pのi番目の要素にマッピングされます。ゼロが一致する配列は配列P0に入力され、残りは配列P1に入力されます。 各配列P0およびP1について、混合(再帰)が実行されます。 シャッフルされた配列は1つに結合されます。 最初に配列P0から要素を取得し、次に配列P1から要素を取得します。
サンデリウス(P)攪拌手順:
1. n := |P|; - ( ) P 2. n=1, P; 3. g:=[gi, i=1..n]; – gi 4. P0:=[]; P1:=[]; - 5. i0:=0; i1:=0; - 6. k:= 0; 7. g[k]=0, 7.1. P0[i0] := P[k]; 7.2. i0 := i0+1; 8. g[k]=1, 8.1. P1[i1] := P[k]; 8.2. i1 := i1+1; 9. k := k+1; 10. k<n, 7. 11. P0 := Sandelius(P0); 12. P1 := Sandelius(P1); 13. P := P0||P1 – . 14. P. 1 n: P=[1,2, …,n]; Sandelius(P);
アルゴリズムのプログラミングは非常に簡単です。
したがって、たとえば、Mapleでプログラミングできます
Sandelius:=proc(p) local A,m,i,p1,p2; m:=nops(p); A:=[seq(getNextRndBit(), i=1..m)]; p1:=[]; p2:=[]; for i from 1 to m do if A[i]=0 then p1:=[op(p1),p[i]]; else p2:=[op(p2),p[i]]; fi; od; if nops(p1)>1 then p1:=Sandelius(p1); fi; if nops(p2)>1 then p2:=Sandelius(p2); fi; return [op(p1),op(p2)]; end proc:
これは、私の研究の1つで使用したC ++でのアルゴリズムの実装例です。
unsigned __int8 *bits,*tmp_perm; Sandelius(unsigned __int8 *perm,int n) { tmp_perm = (unsigned __int8 *)malloc(n); bits = (unsigned __int8 *)malloc(n); for(int i=0;i<n;i++) perm[i]=i; recursiveSandelius(perm,n); free(bits); free(tmp_perm); } recursiveSandelius(unsigned __int8 *perm,int n) { if (n<=1) return; for(int i=0;i<n;i++) bits[i]=getNextRndBit(); k=0; for(int i=0;i<n;i++) if(!bits[i]) tmp_perm[k++]=perm[i]; zeros=k; for(int i=0;i<n;i++) if(bits[i]) tmp_perm[k++]=perm[i]; memcpy(perm,tmp_perm,n); recursiveSandelius (perm,zeros); recursiveSandelius (&perm[zeros],n-zeros); }
特徴
順列を生成するためのアルゴリズムが非常に明確に説明されていることを願っています。 次に、彼の作品の特徴について少し説明します。
操作のために、アルゴリズムはランダムビットのシーケンスを必要とします。 この系列の主な要件はビットが独立していなければならないということです。 この場合、アルゴリズムは均等に分散された順列を生成します。
ランダムビットは不均一な分布を持っている可能性がありますが、それらは独立している必要があります。そうでない場合、置換の分布は均一ではありません。
欠点には、順列の生成に必要なランダムビットの数が事前に決定されていないという事実が含まれます。
練習チェック
前の段落で示された事実は分析的に証明されたとすぐに言わなければなりませんが、実際にそれらをテストしたかったのです。
結果の順列の分布の均一性を確認するために、数学的なパッケージMapleで簡単なプログラムを作成しました。 プログラムでは、多数の順列を生成し、各タイプの順列の数をカウントしました(ヒストグラムのようなもの)。 結果の配列に対して、均一性の仮説はピアソン基準によってテストされました。 さらに、1回のルックアップを生成するために必要なビット数の分布が計算されました。
ここにはプログラムのソースコードを表示するポイントはありませんが、自分でカウントしたい場合は、ソースコードのあるファイルをここで見つけることができます 。
長さn = 7の順列が調査されました。 N = n!* 1000個の順列が生成されました。 ランダムビットは、次のように生成されました。0は確率0.5 + d、1は確率0.5-dです。 均一に分布したビットの場合、dは0です。 依存ビットを取得するために、ランダムビットが生成され、前のビットに追加されました。
妥当な実行時間の理由から、n = 7という数字が使用されます(10〜20分あります)。
| オプション | 同等の代替(ピアソン基準)? | 棒グラフ | ランダムビットの平均数/標準偏差 |
|---|---|---|---|
| 独立ビット、d = 0 | はい | 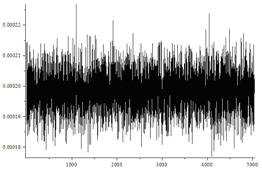 | 28.24 / 28.26 |
| 独立ビット、d = 0.05 | はい | 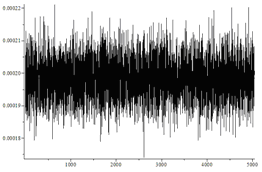 | 28.50 / 28.54 |
| 独立ビット、d = 0.4 | はい | 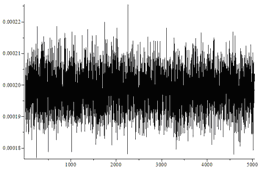 | 71.47 / 74.77 |
| 依存ビット、d = 0.05 | いや | 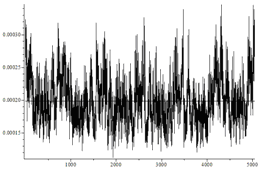 | 30.15 / 30.32 |
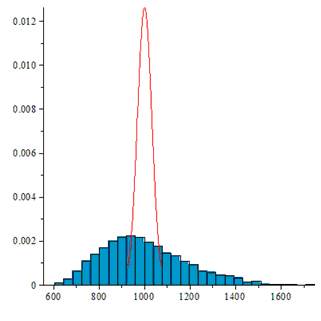
図では、順列の水平方向の数と、それらの発生の垂直方向の頻度がマークされています。 後者の場合、分布は均一とは非常に異なることが肉眼で見ることができます。
また、独立したランダムビットの確率のバイアスに関係なく、アルゴリズムは均一に分散した順列を生成することもわかります。 ただし、確率のバイアスが大きいほど、アルゴリズムが必要とするランダムビットが多くなります。
ビットが依存している場合、生成される置換の分布は均一分布とは異なります。
各タイプの順列の数は、平均N / nで正規分布に近いはずです! 分散N / n!(1-1 / n!)。
最初の3つの場合、ヒストグラムは次のようになります。
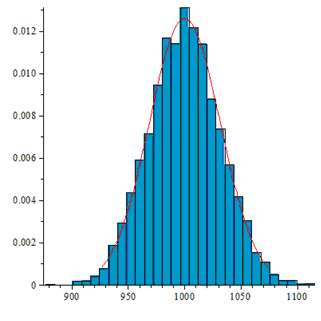
後者の場合、分布は予想からはほど遠いです。
文学
1. M.サンデリウス。 シンプルなランダム化手順、王立統計学会のJ. Ser。 V.、V。24、No。2、1962