💀 👼🏼 🐠 モンテカルロ法とその精度 👇🏽 🌶️ 👩🏼‍🎤

モンテカルロ法は数値解法です。

ランダム変数のモデリングによる数学的問題。メソッドの歴史のアイデアとそのアプリケーションの最も簡単な例は、ウィキペディアで見つけることができます。

メソッド自体に複雑なものはありません。この方法の人気を説明するのはこの単純さです。

このメソッドには2つの主な機能があります。 1つ目は、計算アルゴリズムの単純な構造です。 2番目-計算誤差は通常比例します

$\ sqrt {D \ zeta / N}$ どこで $D \ゼータ$ 一定であり、 $N$ -テストの数。この方法で高精度を達成することは不可能であることは明らかです。したがって、通常、モンテカルロ法は結果がほとんど必要とされない問題を解決するのに特に効果的であると言われています。

ただし、同じ問題は異なる値に対応する異なるバージョンのモンテカルロ法で解決できます $D \ゼータ$ 。多くの問題では、大幅に低い値に対応する計算方法を選択することにより、精度を大幅に向上させることができます $D \ゼータ$ 。

メソッドの一般的なスキーム

未知の数量mを計算する必要があるとします。このようなランダム変数を考えてみましょう $\ xi$ に $M \ xi = m$ 。同時にみましょう $D \ xi = {{b} ^ {2}}$ 。

検討する $N$ 独立したランダム変数 ${{\ xi} ^ {1}}、{{\ xi} ^ {2}}、\ ldots、{{\ xi} ^ {N}}$ （実装）分布が分布と一致するもの $\ xi$ 。もし $N$ 十分に大きい場合、中心極限定理によると、和の分布 ${{\ rho} _ {N}} = \ sum \ limits_ {i} {{{\ xi} _ {i}}}$ パラメータでほぼ正常になります $M \ rho_N = Nm$ 、 $D \ rho_N = Nb ^ 2$ 。

中央極限定理に基づいて（または、Muavre-Laplace極限定理が必要な場合）、関係を取得することは難しくありません。

$P \左（\左| \ frac {{{\ rho} _ {N}}} {N} -m \右| \ le k \ frac {b} {\ sqrt {N}} \右）= P \ left（\ left | \ frac {1} {N} \ sum \ limits_ {i} {{{{xi} _ {i}}}-m \ right | \ le k \ frac {b} {\ sqrt {N }} \右）\〜2 \ Phi（k）-1$

どこで $\ファイ（x）$ 標準正規分布の分布関数です。

これは、モンテカルロ法にとって非常に重要な関係です。また、計算方法も示します。 $m$ 、およびエラー推定。

実際、私たちは見つけます $N$ ランダム値 $\ xi$ 。示された関係から、これらの値の算術平均はほぼ等しいことがわかります。 $m$ 。に近い確率で $（2 \ Phi（k）-1）$ そのような近似の誤差は超えない $kb / \ sqrt {N}$ 。明らかに、このエラーは成長とともにゼロになる傾向があります。 $N$ 。

目標に応じて、最後の比率はさまざまな方法で使用されます。

k = 3をとると、いわゆる「ルール $3 \シグマ$ 」：

$P \左（\左| \ frac {{{{\ rho} _ {N}}} {N} -m \右| \ le 3 \ frac {b} {\ sqrt {N}} \右）\約0.9973 。$
特定のレベルの計算の信頼性が必要な場合 $\アルファ$ 、

$P \左（\左| \ frac {{{{\ rho} _ {N}}} {N} -m \右| \ le \左（{{\ Phi} ^ {-1}} \左（（1 + \ alpha）/ 2 \ right）\ right）\ frac {b} {\ sqrt {N}} \ right）\およそ\ alpha$

計算精度

上記の関係からわかるように、計算の精度はパラメーターに依存します $N$ と数量 $b$ -確率変数の標準偏差 $\ xi$ 。

この段落では、2番目のパラメーターの重要性を示したい $b$ 。これは、例によって最もよく示されています。特定の積分の計算を検討してください。

特定の積分の計算は面積の計算に相当し、積分を計算するための直感的なアルゴリズムを提供します（Wikipediaの記事を参照）。より効果的な方法を検討します（ただし、Wikipediaの記事にも記載されている式の特殊なケース）。ただし、一様に分布した確率変数の代わりに、同じ間隔で与えられたほぼすべての確率変数をこの方法で使用できることを誰もが知っているわけではありません。

したがって、特定の積分を計算する必要があります。

$I = \ int \ limits_ {a} ^ {b} {g（x）dx}$

任意のランダム変数を選択してください $\ xi$ 分布密度 ${{p} _ {\ xi}}（x）$ 間隔で定義 $（a、b）$ 。そして、ランダム変数を考えます $\ zeta = g（\ xi）/ {{p} _ {\ xi}}（\ xi）$ 。

最後のランダム変数の数学的期待値は次のとおりです。

$M \ zeta = \ int \ limits_ {a} ^ {b} {[g（x）/ {{p} _ {\ xi}}（x）] {{p} _ {\ xi}}（x）dx = I}$

したがって、以下を取得します。

$P \左（\左| \ frac {1} {N} \ sum \ limits_ {i} {{{\ zeta} _ {i}}}-I \右| \ le 3 \ sqrt {\ frac {D \ゼータ} {N}} \右）\約0.9973。$

最後の関係は、選択した場合 $N$ 値 ${{\ xi} ^ {1}}、{{\ xi} ^ {2}}、\ ldots、{{\ xi} ^ {N}}$ 、そして十分に大きい $N$ ：

$\ frac {1} {N} \ sum \ limits_ {i} {\ frac {g（{{\ xi} _ {i}}）} {{{p} _ {\ xi}}（{{\ xi} _ {i}}）} \約I}$

。

したがって、積分を計算するには、ほぼすべてのランダム変数を使用できます $\ xi$ 。しかし、分散 $D \ゼータ$ 、および精度評価は、どのランダム変数に依存します $\ xi$ 計算に使用します。

それを示すことができます $D \ゼータ$ 最小値を持つのは ${{p} _ {\ xi}}（x）$ | g（x）|に比例します。この値を選択してください ${{p} _ {\ xi}}（x）$ 一般的な場合、それは非常に難しい（複雑さは解決される問題の複雑さに等しい）が、この考慮によって導かれる価値がある。積分可能な関数のモジュールに似た形式の確率分布を選択します。

数値例

理論はもちろん良いことですが、数値の例を見てみましょう。 $a = 0$ ; $b = \ pi / 2$ ; $g（x）= cos（x）$ 。

2つの異なるランダム変数を使用して積分値を計算します。

最初のケースでは、[a、b]に一様に分布したランダム変数を使用します。つまり、 ${{p} _ {\ xi}}（x）= 2 / \ pi$ 。

2番目のケースでは、[a、b]に線形密度を持つランダム変数を取ります。つまり、 ${{p} _ {\ xi}}（x）= \ frac {4} {\ pi}（1-2x / \ pi）$ 。

以下は指定された関数のグラフです

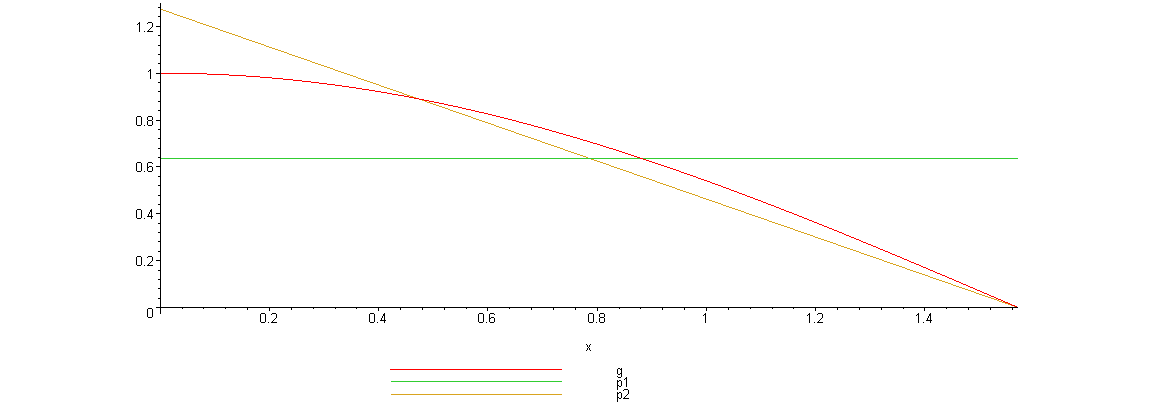
線形密度が関数によりよく対応していることが簡単にわかります $g（x）$ 。

Maple数学パッケージのモデルコードプログラムコード

restart; with(Statistics): with(plots): #  g:=x->cos(x): a:=0: b:=Pi/2: N:=10000: #  p1:=x->piecewise(x>=a and x<b,1/(ba)): p2:=x->piecewise(x>=a and x<b,4/Pi-8*x/Pi^2): # plot([g(x),p1(x),p2(x)],x=a..b, legend=[g,p1,p2]); #   I_ab:=int(g(x),x=0..b); #  -      #       INT:=proc(g,p,N) local xi; xi:=Sample(RandomVariable(Distribution(PDF = p)),N); evalf(add(g(xi[i])/p(xi[i]),i=1..N)/N); end proc: #   I_p1:=INT(g,p1,N);#c   I_p2:=INT(g,p2,N);#c   #  Delta1:=abs(I_p1-I_ab);#c   Delta2:=abs(I_p2-I_ab);#c   #    delta1:=Delta1/I_ab*100;#c   delta2:=Delta2/I_ab*100;#c   #  Dzeta1:=evalf(int(g(x)^2/p1(x),x=a..b)-1); Dzeta2:=evalf(int(g(x)^2/p2(x),x=a..b)-1); #     3*sqrt(Dzeta1)/sqrt(N); #     3*sqrt(Dzeta2)/sqrt(N);

このプログラムのファイルはここで取得できます

積分の正確な値は分析的に簡単に計算でき、1に等しくなります。

での1つのシミュレーションの結果 $N = 10$ ：

一様分布のランダム変数の場合： $私\約1.21666$ 。

線形分布密度のランダム変数の場合： $私は約0.97641$ 。

前者の場合、相対誤差は21％を超え、後者の場合は2.35％です。精度 $3 \ sqrt {\ frac {D \ zeta} {N}}$ 最初の場合は0.459で、2番目の場合は0.123です。

このモデルの例は、モンテカルロ法でランダム変数を選択することの重要性を示していると思います。正しいランダム変数を選択すると、少ない反復回数で計算の精度を高めることができます。

もちろん、1次元積分はこの方法では計算されません;これには、より正確な求積式があります。しかし、状況は多次元積分への移行によって変わります。なぜなら、求積式は面倒で複雑になり、モンテカルロ法はわずかな変更のみで適用されます。

反復回数と乱数ジェネレーター

計算の精度が数量に依存することを確認するのは難しくありません $N$ 量に含まれるランダム変数。さらに、計算の精度を10倍にするには、増やす必要があります $N$ 100回。

いくつかの問題を解決するとき、許容可能な推定精度を得るために、非常に多数の $N$ 。また、この方法は非常に迅速に機能することが多いため、後者を最新のコンピューティング機能で実装することはまったく難しくありません。そして、誘惑は単に数を増やすことです $N$ 。

何らかの物理現象（物理乱数センサー）がランダム性の原因として使用される場合、すべてが正常に機能します。

多くの場合、擬似乱数センサーはモンテカルロ計算に使用されます。そのような発電機の主な特徴は、特定の期間の存在です。

モンテカルロ法は値とともに使用できます $N$ 擬似乱数ジェネレータの期間を超えない（できればずっと小さい）こと。後者の事実は、シミュレーションで使用されたランダム変数の独立条件から得られます。

大規模な計算を行うときは、乱数ジェネレーターのプロパティでこれらの計算を実行できることを確認する必要があります。標準的な乱数ジェネレーター（ほとんどのプログラミング言語）では、ほとんどの場合、オペレーティングシステムの処理能力が2を超えず、それ以下です。このようなジェネレーターを使用する場合、非常に注意する必要があります。 D. Knutの推奨事項を調べて、独自のジェネレーターを構築することをお勧めします。ジェネレーターは、事前に十分に知られた十分に長い期間があります。

文学

1968年の数学に関する一般的な講義。第46号。SobolI.M. モンテカルロ法。 M。：Nauka、1968 .-- 64 p。

モンテカルロ法とその精度

メソッドの一般的なスキーム

計算精度

数値例

反復回数と乱数ジェネレーター

文学

More articles: