コンピューターゲームでのMatAnalysisの使用（パート2）

キーワード： 収集の問題。 Wolfram Alpha; Wolfram Mathematica; 第2種のスターリング数。 分析; 確率論; マットの期待; 中央値; 変位値; コンピューターゲーム; 挿入物のコレクション。 確率変数の分布関数。 確率密度、ArcheAge。

はじめに

コレクション全体（BomBimBomまたはTurboチューインガムインサート、またはコンピューターゲームキャラクター用の重装甲のセット）を収集するために100個のアイテムのうち3個のみを取得することが残っている場合、目の炎と奇跡の期待が頭から数学的分析の論理と理由を押し出します。 「もう少しすれば、あとは残ります！」という考えが1つだけあります。 全部集めます！」 現時点では、この取りつかれたコレクターの親relativeや友人は、「ああ、少し、いくら？」という1つの質問だけで困惑していました。 お母さんは嫌いなチューインガムをもっと買う必要がありますか、それともボーイフレンドがゲーム「バアルの最も珍しいche病者」でモンスターを倒すまで、女の子はどれだけ一人で座る必要がありますか？

Yandexを使用しても、「通常の」検索エンジンのクエリ自体を作成することは難しいため、「N個のライナーの完全なコレクションを組み立てるにはチューインガムがどれだけ必要か」という質問に答えることは非常に困難です。 自分で問題を解決しようとすると、通常、人々は立ち往生します-どの方法でアプローチするかは明確ではありません。

この記事では、次の3つの質問に対処します。一見したところ明確でないタスクへのアプローチ方法、解決方法。 （eBayで2次方程式の式を購入するというオファーを受け取るのではなく）科学的な質問に対する科学的な答えを受け取るために使用する検索エンジンの種類は何ですか？ そしてもちろん、ルーズリーフのコレクションを組み立てるのにどれくらいのチューインガムが必要ですか？

記事のナビゲーション

記事はかなり大きいことが判明しました。 したがって、何かをスキップできる場所では、報告します。 このような章では、問題の解決策ではなく、問題の解決に使用される概念と原則を扱います。 詳細が面白くなったら、後で見逃した場所を読み直すことができます。 問題の言葉遣いをよく理解しておけば、すぐに答えを知りたい人はすぐに結果を見ることができます。 ただし、 Alpha Wolframの章を個別に読むことをお勧めします。

また、便宜上、章の完全なリストを示します。

1. 問題の声明
2. 男の子、女の子、ボール
3. 取りつかれたコレクターの数学的モデリング
4. 好奇心が強いテーブル
5. 私はアルファウルフラムです
6. 数学探偵
7. 300年前
8. 三行
9. 2つのエンティティ
10. 医師の平均患者体温と平均給与
11. 直接登らない場合は横に行きます
12. 何らかのウィキ
13. 結果
14. 誕生日とカビの銀行
15. 結論

問題の声明

数学の厳密さを愛する人と、それに精通していない人の両方に明確にするために、コレクションの問題を2つの方法で定式化します。

1. （子供の頃から馴染みのある言語を通して）各チューインガムにK個のゆるい葉の1つが等しい確率で含まれるようにします。 N個のチューインガムを購入した場合、ライナーのコレクション全体を収集する可能性はどのくらいですか（K個のユニークなライナーがあります）。
2. （より科学的な言語で） K個の基本的な結果のセットを与えてみましょう（すべての結果は同様に可能性があります）。 N回の実験後、各イベントが少なくとも1回発生する可能性はどのくらいですか？

将来的に役立つ多くのポイントをすぐに明確にします。 まず、簡単にするために、コレクションのすべての要素に1からKまでの番号を付けます。したがって、単純に番号を扱います。 第二に、基本的な結果は長さNのシーケンスであり、K個の異なる番号で構成されます。 たとえば、K = 3およびN = 5の場合、シーケンス{3,3,1,2,3}、{1,2,3,3,3}、{3,3,1,1,1}は次のいずれかです。可能な結果、要素の順序が重要です。 そのようなシーケンスですべてのK番号が少なくとも1回発生する場合、これは「成功した」シーケンスを意味し、発生しない場合、少なくとも1つの番号は発生せず、シーケンスは成功しません。 さらに、可能なシーケンスも同様に考えられます。 第三に、順序が重要であれば、可能なすべてのK数のシーケンスの数、N要素の長さを常に計算できます。 この金額はK ^ Nです。 4番目に、Nステップでコレクションを収集する確率は、「成功した」シーケンスの総数に対する比率、つまりK ^ Nに等しい。 したがって、確率または非常に多くの「成功した」シーケンスのいずれかを検索できます-より便利なため、一方は常に他方から取得できます。

男の子、女の子、ボール

「注文事項」と「数量がK ^ N」に疑問を持たない人、および「階乗」と「nからkまでのC」が何であるかを覚えている人は、 この章を飛ばし て次へ進む ことができます 。 組み合わせ論を完全に忘れた人、またはまだ慣れていない人のために、重宝する主なポイントを考慮してください。

コンビナトリクスの歴史は、古代に根ざしていましたが、ゲーマーのおかげで依然として活発に発展しました。 カルダノ、ガリレオ、ファームパスカル、およびこの世界の他の偉大な頭脳自体は、熱心なゲーマーではありませんでした（事実ではありませんが）、少なくともゲーマーは、ゲーム、勝利戦略、およびガイドに執筆を依頼しました。 もちろん、サイコロとカードを2回以上プレイした後、戦車や魔法を使ったギャンブルのファンはあまりいませんでした。 片方では不足があり、もう片方では燃えた。 しかし、パズルやギャンブルの分析に積極的に適用することにより、組み合わせ論は数学のほぼすべての分野で実際的な問題を解決するのに非常に役立つことが判明しました。 さらに、組み合わせ手法は、統計学、プログラミング、遺伝学、言語学、および他の多くの科学で長い間有用であることが証明されています。 ウィキペディアは悪です（これは何度も覚えています）が、式に関係のない概要を読むことは物理的に可能ですが、信頼するべきではありません。 それにもかかわらず、あなたは記事「コンビナトリクスの歴史」を読むことができます

組み合わせ論に関するさまざまな資料を探していたときに、あるサイト 、またはこのサイトのドキュメントの 1つに出会いました。 書かれている言語が好きだったので、そこで組み合わせ論に慣れることができます。 一般的に、このサイトについては覚えていませんが、1つの「しかし」ではありません。 軌道についてのタスクがあります。 私はそれが本当に好きで、面白そうに見えたので、今それを見て、コレクションの問題を解決する方法を考えましたが、それについては後で詳しく説明しました。

便利になる組み合わせ論の重要な事実を以下に示します。

1.）基数Kの番号体系には、合計N桁の数字がいくつありますか？ K国の代表者をN席に配置する方法はいくつありますか？ K個の異なる色のフェルトペンがある場合、N個の正方形に色を付けるにはいくつの方法がありますか？ 異なる色の数Kと1つのボールだけが各ボックスに収まる場合、N個のボックスをカラフルなボールで満たす方法はいくつありますか？

これらすべての質問に対する答えは同じです-「繰り返しのある配置」。 ボールの場合、最初のボックスにK色のボールを置くことができます。 つまり、1つのボールを最初のボックスに入れるためのKオプションがあります。 2番目のボックスでは、K個の方法でボールを貼り付けることもできます。 最初と2番目のボックスをボールで満たすオプションは、すでにK * K = K ^ 2です。 これは、最初のボックスの塗りつぶしオプションごとに、2番目のボックスを塗りつぶすためのKオプションのいずれかがあるためです。 N個のボックスがある場合、K ^ N個のオプションがあることを意味します。

2.）数値の各桁が1回だけ出現するように、基数Nの数値システムには合計N桁の数値がいくつありますか？ それぞれの国の代表が座るように、Nの国の代表をN席にどのように配置できますか？ 異なる色のフェルトペンがN個あり、各フェルトペンが使用される場合（もちろん再描画なし）、N個の正方形に色を付ける方法はいくつありますか？ N個のボールをN個の箱に入れるにはいくつの方法がありますか？

これらすべての質問に対する答えは、「順列」です。 一般に、ボールと数字のあるケースは、言葉遣いにおいても同じです。 そもそもN個のボールを置くことができます。 2番目の場所には残りのN-1ボールがあり、3番目の場所には最初の2つの場所N-2ボールを埋めた後の残りのいずれかがあります。 そして最後まで続きます。 製品N *（N-1）*（N-2）*（N-3）* ... *（N-（N-2））*（N-（N-1））があることがわかります。 1からNまでのすべての自然数のこの積は、階乗と呼ばれます。 そして、「N！」と指定されています。 はい、感嘆符、これは階乗または1からNまでのすべての自然数の積の指定です。それはどこでもどこでも非常に頻繁に見られます。製品としてそれを書くのはかなり長い時間であるため、記録を感嘆符アイコンに簡略化して短縮することにしました。 階乗についての古いジョークがありますが、それは教師が伝えたいことです。

マタン試験では、講師は学生にテイラーシリーズに出展者を配置するように依頼します。

学生：1つに分割された1つのプラスx（大声で厳soleに発音します）+ 2で割ったx 2（同じく大声で）+ 3で割った立方体のx

講師：わかった、わかった、そうだ、でもなぜそんなに叫んでいるの？！

学生：そうですね、感嘆符もそうです!!!

ゼロからの階乗が1になることに注意してください。0！= 1

3.） N個のK個のボックスに番号付きボールを充填する方法はいくつありますか？ （箱よりもボールが多い）あなたはNの映画のチケットとKのガールフレンドを持っています。 友達にチケットをいくつ渡すことができますか？ （ガールフレンドよりチケットが多い）

これらの質問に対する答えは、「繰り返しのない配置」です。 ただし、この決定は最初の段落ではなく、2番目の段落に似ています。 そもそもN個のボールを置くことができます。 2番目の場所には残りのN-1ボールがあり、3番目の場所には最初の2つの場所N-2ボールを埋めた後の残りのいずれかがあります。 箱がなくなるまで続けます。 したがって、製品はN *（N-1）*（N-2）*（N-3）* ... *（N-（K-1））になります。 つまり、K + 1からNまでのすべての自然数の積です。しかし、そのような積はN *（N-1）*（N-2）*（N-3）* ... *（N-（K-1））の形式でペイントできます。 *（NK）！ /（NK）！ = N！/（NK）！ 一般的に、これははるかに短いです。

4.）最後の段落は、順序が重要な場合と重要でない場合がある理由についてです。 そして、「nからkへのC」とは何ですか。

あなたがUAZを持っていて、友達と釣りに行くとしましょう（男だけ、女はいません）。 UAZはK人に合うことができます。 そして、あなたのすべてにはN.の友人がいますあなたのUAZに合わない人は誰でも他の車で行きます。 友達にUAZを埋めるにはいくつの選択肢がありますか？ 現在オンラインになっている20人（N）の友人のうち、5人（K）のチームを集めてDotAを1時間プレイする方法はいくつありますか？ （もちろん、微妙なニュアンスがあります-あなたを考慮するかどうか、しかし私たちはこれを気にしません）

この例と以前のすべての例の違いは何ですか？ その順序は重要ではありません。 UAZに誰が、どのように、どこに座るか、またはあなたが最初に誰であり、誰がチームの2番目に電話するかは、何の役割も果たしません。 主なものは構成であり、誰がどこにいるのかはもはや重要ではありません。 順序が重要な場合は、前のオプションとまったく同じになります。つまり、答えはN！/（NK）！になります。 しかし、順序は重要ではありません。 そして、例2）階乗の順序について。 それはN！/（NK）！ K！で除算する必要があります。次に、シーケンスのみが異なり、構成は同一であるケースを「1つのバリアントに折りたたむ」必要があります。 たとえば、3人と2つの場所があるとします。 次に、すべての可能なオプション。 たとえば、3は{1,2}、{1,3}、{2,1}、{2,3}、{3,1}、{3,2}になります。 それは6つのオプションです。 3！/（3-2）！= 3！/ 1！= 3！= 6。 しかし、UAZを使用した例では（二重のものはすでにUAZになっています）、シーケンスは重要ではないため、{1,2}や{2,1}などのオプションは同じです。 まあ、本当に、UAZのPetyaとVasyaまたはVasyaとPetya-違いはありません。 主なことは、二人がそれに乗ることです。 順序が重要ではない段落4の答えは、式N！/（NK）！/ K！であることがわかります。 そして、そのような場合は、順序が重要ではなく、「NとKの組み合わせ」という構成だけが重要なときに呼び出されます。 この奇跡の公式には別の名前があります-「二項係数」。 しかし、ほとんどの場合、「nからkへのC」と呼ばれます。 （「Tse from en po ka」）。 それは、それぞれ下側と上側のインデックスnとkを持つ文字Cでそれぞれ示されます。 二項係数は、よく知られているニュートン二項に最も直接関係しています。 複雑なことは何もありません。どこでも好きな場所で読むことができます（Wikipediaでのみ主要なことを読んでください）。 ニュートンの二項係数と二項係数は基本的に非常に単純ですが、それらが非常に多くの異なる状況で突然適用されることが判明したという事実は、一種の神秘的なハローと、これがすべて正当な理由による疑いを生み出します。 複雑なことはありませんが、興味深いことがたくさんあります

この段階での組み合わせ論からのこの知識は十分であり、残りは途中で説明されます。

取りつかれたコレクターの数学的モデリング

最初に問題を分析的に解決しようとして、（もちろん徹底的な検索ではなく、数式によって）可能なすべての満足できるシーケンスを数えようとして、私は何も起こらなかったことを告白します。 より正確には、推論の道筋は非常に論理的でしたが、最終的に私は巨大な和の合計を書く必要があり、それはコンパクトなものに崩壊することはできませんでした。

特定のプロセスの基本原則は理解できるが、同時にこのプロセスを説明する分かりやすく消化可能な法則を得ることができない場合（何がどのように起こっているのかを理解しているが、全体の式を書き出すことができない場合）、反対から行くことができます-このプロセスをシミュレートし、数値解を取得し、答えを分析してみてください。 たとえば、最も優れた分析方法である「注視方法」を使用します。 その後、新しいデータ、アイデア、思考が解決策を教えてくれる可能性は十分にあります。

これは、問題の本で答えをスパイし、その下にソリューションを収める方法です。 当時はそれを使用していましたが、同時にそのことを認めませんでした。 しかし、物理学セミナー（彼も講師を務めていました）は、これは絶対に普通であり、さらに物理学はある程度「フィッティングの技術」であると説明しました。 非常に多くの場合、最初にいくつかの新しい現象が発見され、それを説明しようとします。つまり、現象の理論的な実証を実験データに適合させようとします。 それから私たちには完全に明確ではありませんでした-私たちは「問題を正直に解決する」必要性に慣れています。 ここだけが仮説の理論的構築であり、それに続いて実験的検証が行われます。これは一つのことですが、逆問題がより一般的です。 そして、一般的に言えば、一方が他方なしでは存在しません。 実践から初期データを受け取っていない場合に構築する理論は何ですか？

覚えておくべき主なこと-答えに答えを当てはめることは、通常のことだけでなく、自然で良いことです。 そのようなノーベルのために。 アインシュタインは光電効果を予測しなかった、と彼は説明した。 しかし、限られた光速に関連するさまざまな効果の彼の予測のために、彼はノーベルを受け取りませんでしたが、はい-それはまさにその予測でした。 また、科学分野の賞のリストを見ると、「説明のために...」「理解への貢献のために...」という文言が非常に多く使われています。

したがって、式の導出方法に関するアイデアがないため、モデルを作成します。

Wolfram Mathematica環境でシミュレートします。 Mathematicaは非常に使いやすく、高速で、素晴らしく、直観的なインターフェースです（ただし、Ctrl + Enterを知っている必要があることを除いて-これは、現在のコードの実行を開始するための組み合わせです。メインとメイン）、そして最も重要なのは、90％例から+関連リンクの束。 ヘルプ自体の中の本当に便利なリンクなので、インターネットのようにサーフィンにこだわってそこから始めることもあります。 データを表示するのは非常に簡単で簡単です-あらゆる種類のグラフ、テーブルを作成し、おそらくあらゆる場面で、プレゼンテーションにとっては非常に貴重です。 インストールして試してください-スティックすれば後悔することはありません。

ところで、この記事のすべての写真はWolfram Mathematicaで作成されました。

40個のアイテムのコレクションをシミュレートするコードを次に示します。 コードには多くのコメントがあります。 アルゴリズム自体は、読み取り中にできる限り明確になるように記述されていますが、同時に、速度が低下しています。 私は10万回の反復で10分間働きます。

(*   *) SeedRandom[1234];(*"".      ,      ,        .  ,        .*) NPosibleElems=40;(*    *) WhatWeHave=Table[0,{i,1,NPosibleElems}];(*   .       "  ".     1,      0.         ,         *) WhatWeWantToHave=Table[1,{i,1,NPosibleElems}];(*    .       "  ".      1,      0.           ,   - ,          *) TargetArray=BitOr[WhatWeHave,WhatWeWantToHave];(*         ,           ,        .      .     ,      *) NumItearations=100000;(*    .     -  -  .*) FinishedSteps=Table[0,{i,1,NumItearations}];(*  ,           . "  "    .*) ProgressIndicator[Dynamic[indic],{1,NumItearations}](*       .      ,     .  indic    .       ,          .        -    .   ,  .*) For[j=1,j<=NumItearations,j++, (*    .*) indic=j;(*  ...       ,     ,    .       ,     *) FindedElems=WhatWeHave;(*FindedElems -  .  "" .           *) While[ Total[TargetArray-FindedElems]!=0,(*  .           .            ,                  -       .*) NewItem=RandomInteger[{1,NPosibleElems}];(*  ,     *) If[FindedElems[[NewItem]]!=1,FindedElems[[NewItem]]=1];(*     -    *) FinishedSteps[[j]]+=1;(*    *) ]; ]; (*  (     ).      *) {bins,count}=HistogramList[FinishedSteps]; HistoList=Transpose[{binsN[[2;;]],count}]; TickL=20; Show[{Histogram[FinishedSteps],ListPlot[HistoList,PlotStyle->{Darker[Red],PointSize[Large]}]},Ticks->{Table[i,{i,0,Last[bins],TickL}],Automatic}] (*  *) ProbList=Transpose[{bins[[2 ;;]],count/NumItearations}]; ListLinePlot[ProbList]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

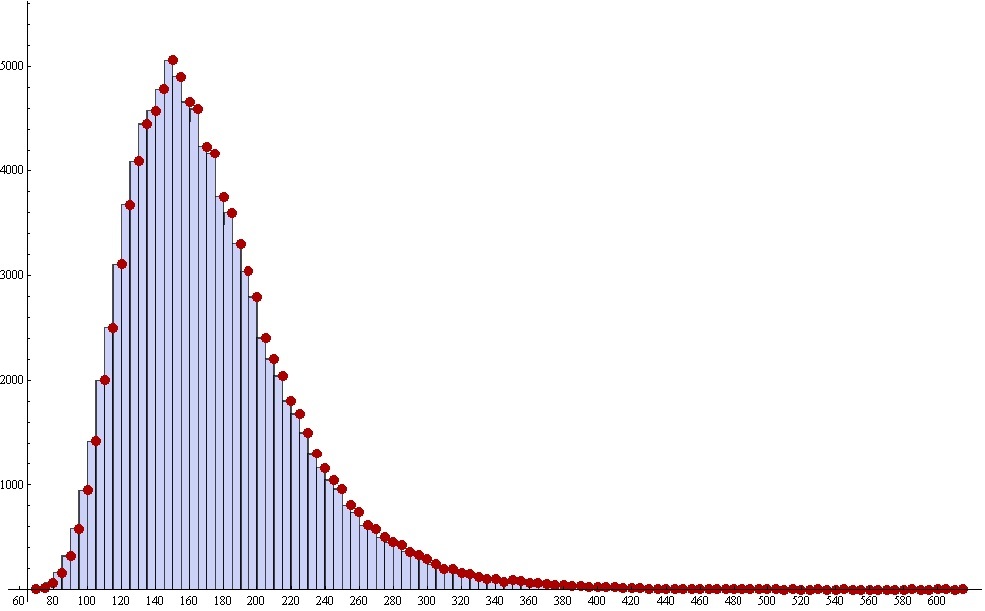
その結果、まさにそのような写真が得られます。 これはヒストグラムです。 その中で、各列には、水平軸上の独自の座標、独自の高さと幅があります。 列の高さは、100,000回の反復のうち、コレクションがnステップで完了した回数を示します。この場合、nは水平軸上の座標です。 おおまかにですが、一般的にはそうです。 より正確には、列の幅について覚えておく必要がありますが、それはそのようなものではありません。 事実は、ヒストグラムを作成するとき、「適切な」列幅の選択はアーカイブおよびアーカイブの複雑さの問題です。 それを選択して完成した結果を表示するとき、実際には、列の高さは、列の左境界より大きく、右境界より小さい座標を持つイベントが発生した回数を示すことを覚えておく必要があります。 原則として整数のみが可能で、仮に列の幅を0.25にしたとしましょう。 その結果、「滑らかな」画像の代わりに、穴のあるフェンスのような列の「櫛」が得られます。つまり、列、それからいいえ、つまりいいえです。 非常に大きな幅をとる場合、非常に幅の広い列を1つだけ取得できます-それからは意味がありません。 すべての曲がりとニュアンスは単純になくなります。

列の高さは、すべての試行のうち、コレクションが特定のステップ数（チューインガムを開く）で収集された回数を示します。 特定のステップでコレクションを取得する確率を見つけるには、列の高さをテストの総数で割る必要があります。したがって、コレクションの問題に対する数値モデル化された答えが得られます。

既に述べたように、誤って軌道に関するタスクに遭遇した後（上記のリンクを参照）、アルゴリズムを最適化するだけでなく、最終的に式を推測するのに役立つアイデアが生まれました。

好奇心が強いテーブル

収集プロセスの各瞬間は、一意の要素の数と繰り返しの数という2つの数字で表すことができます。 次回新しい要素を受け取ったときにコレクションの一意の要素を取得する確率は （まだ挿入物を受け取っていない新しいチューインガムで） 、すでに持っている要素に依存するのではなく、独自の要素の数と要素の数だけに依存しますコレクション。



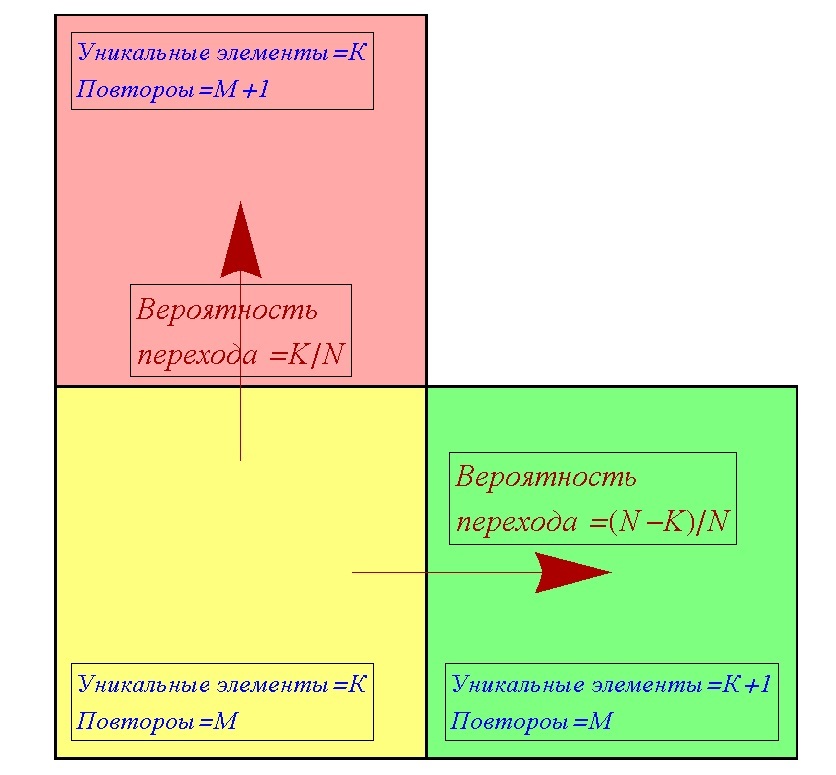
ある時点で、K個の一意の要素があり、M個の繰り返しがあり、合計でコレクションにN個の要素があるとします。 繰り返しの回数は、現在のセット全体から一意の要素を1つだけ削除した場合に残るすべての要素を指すことを明確にする価値があります。 たとえば、リンゴが4つ、梨が3つあり、合計2つの固有の要素がリンゴと梨であり、7回の繰り返しがリンゴ3つと梨2つです。 新しい要素を受信すると、現在の状態（K、M）から他の2つの状態のいずれかに移行できます。 一意の要素の数（K + 1、M）を増やすか、繰り返しの数（K、M + 1）を増やします。 したがって、あらゆるケース（K、M）の変換テーブルを作成できます。



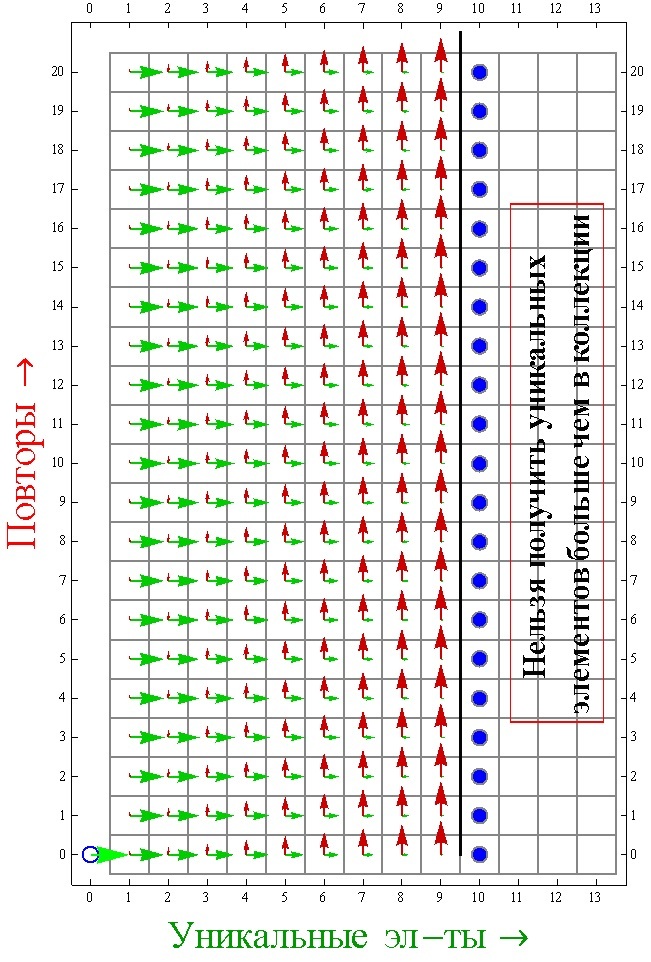
このアプローチに基づいて、収集プロセスをシミュレートするアルゴリズムを構築できます。 次に、各ステップで、確率（N –K）/ Nでセルに移動する（K + 1、M）か、確率K / Nでセルに移動する（K、M + 1）が必要で、K < N. KがNと等しくなると、コレクションがアセンブルされ、必要なステップ数を見つけるためにKとNを追加するだけで済みます。 遷移K / Nおよび（N –K）/ Nの確率は、繰り返しを取得する確率がコレクション内の要素の総数に対する既存の一意の要素の比率に等しく、一意の要素を取得する確率がコレクション内の要素の総数に対する欠損要素の数の比率に等しいという事実によって説明されます。 これは、セル（状態）に入る確率ではなく、セル間の遷移の確率を記述することに注意してください。

このアルゴリズムの実際のコードは次のとおりです。 最初のオプションよりも高速に動作します。

 SeedRandom[1234];(*"".      ,      ,        .  ,        .*) NPosibleElems=40;(*    *) NumItearations=100000;(*    .     -  -  .*) Results=Table[0,{i,1,NumItearations}];(*  ,           . "  "    .*) ProgressIndicator[Dynamic[indic],{1,NumItearations}](*       .      ,     .  indic    .       ,          .        -    .   ,  .*) For[i=1,i<=NumItearations,i++,(*    .*) indic=i;(*  ...       ,     ,    *) n=0;(*       *) m=0;(*      .     2   3 ,      2 - {, }.     3 -        .*) While[n<NPosibleElems,(*  .           .            ,                  -       .*) r=RandomInteger[{1,NPosibleElems}];(*            ,    ,            .*) If[r> n,n+=1,m+=1];(*  n/NPosibleElems    ,    1-n/NPosibleElems  -  .*) ]; Results[[i]]=n+m;(*    ,        ,    -  ( )        *) ]; (*      .*) {bins,count}=HistogramList[Results]; HistoList=Transpose[{binsN[[2;;]],count}]; TickL=20; Show[{Histogram[Results],ListPlot[HistoList,PlotStyle->{Darker[Red],PointSize[Large]}]},Ticks->{Table[i,{i,0,Last[bins],TickL}],Automatic}] (*  *) ProbList=Transpose[{bins[[2 ;;]],count/NumItearations}]; ListLinePlot[ProbList]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、アイデアをさらに発展させます。 固定（K、M）でセルに入るために存在するオプションの数を計算してみることができます。 セル（K、M-1）またはセル（K-1、M）からセル（K、M）を入力できます。 一意の要素が1つだけであるか、繰り返しがない場合、つまりK = 1、M = 0の場合を除き、2つの方法のいずれかでのみそれらにアクセスできます。 セルに入る方法の数（K、M）をV [K、M]と表記します。 セル（K、M-1）からセル（K、M）まで、異なるオプションでKに到達できます。これは、既に一意の要素と同じ数のオプションを繰り返し取得できるためです。 別の隣接セル（K-1、M）から、オプションの数だけ（N-（K-1））をセル（K、M）に取得できます。これは、セル（K-1、M）に一意の要素（K-1 ）、それに応じて（N-（K-1））要素が不足しています。 一般に、セル（K、M-1）を介してセル（K、M）に入るオプションは、V [K、M-1] * Kバリアント、つまり、オプションの数の積がまさに（K、M-1）回になる（K、M-1）から（K、M）に取得するオプションの数。 同様に、セル（K-1、M）からセル（K、M）に入るオプションを使用すると、V [K-1、M] *（N-（K-1））が得られます。 合計すると、セル（K、M）に入るために、オプションの数でV [K、M-1] * K + V [K-1、M] *（N-（K-1））を取得できます。 したがって、セルに入る方法の数（K、M）について非常に有用な式が得られます。

V [K、M] = V [K、M-1] * K + V [K-1、M] *（N-（K-1））



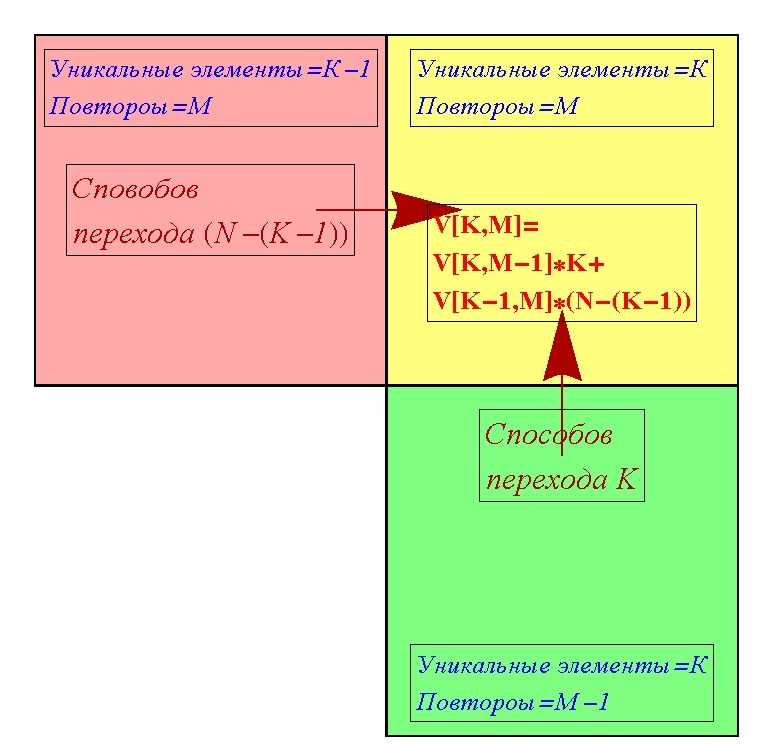
このルールを使用して、任意のセル（K、M）のヒットメソッドの数を順番に計算できます。 つまり、特定の（K、M）のオプションの値をすぐに与える式ではありませんが、数値モデリングではなく、シンボリックな回答を含むテーブルが作成されます。 これがアルゴリズムそのものです。

 KKT=10; MMT=10; V=Table[0,{k,1,KKT},{m,1,MMT}]; V[[1,1]]=NN; For[k=2,k<=KKT,k++,V[[k,1]]=FullSimplify[V[[k-1,1]]*(NN-(k-1))]]; For[m=2,m<=MMT,m++,V[[1,m]]=NN]; For[k=2,k<=KKT,k++, For[m=2,m<=MMT,m++, V[[k,m]]=V[[k-1,m]]*(NN-(k-1))+V[[k,m-1]]*k; ]; ]; MatrixForm[V]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、結果のテーブルは、その巨大なサイズにもかかわらず、注目すべき機能を備えています。 表のすべての列は、最初の列に対するいくつかの数値係数に比例しています。 そして、これらの数値係数は、コレクション内の要素の数に依存しません。 このテーブルのすべての列を最初の列に分割すると、この結果が得られます。



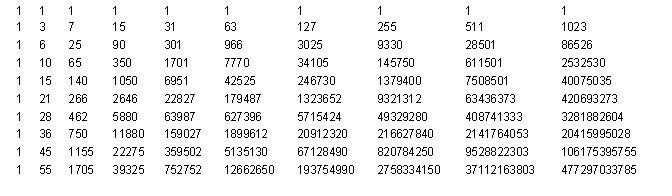
正直に言って、最初に受け取ったとき、私は非常に困惑していました。 とても美しく、信じられないほどに思えたので、私の頭に収まりませんでした。 これらの数は、コレクション内の要素の数に依存せず、繰り返しの数と一意の要素、つまり（K、M）にのみ依存します。 これらの数値がどのように取得されるかを理解すれば、問題は完全に解決され、非常に単純な式になります。 しかし、どのような数字か、私には分かりませんでした。

私はアルファウルフラムです

いくつかの計算中に、5.01326などの特定の係数に直面することを想像してください。 絶対的な正確さでは得られなかったが、考えてみると、突然この数字はなんとなく「美しい」ものであり、よく知られた数学定数で表現されているか、何らかの自然数、対数、サインの根です。 まあ、またはそうでない場合は、非常に近いです。 たとえば、他の誰かのコードを分析するときに、定数のリストはあるがコメントなしでそのような必要性に遭遇する可能性があります。 この場合、 Wolfram Alphaが私を助けてくれました。

以下は、番号5.01326に対する要求への応答の例です 。 （8 * Piのルートを作成しました）

Wolfram Alphaを検索エンジンと呼ぶのは難しいと思いますが、それはそれ以上です。 彼はあなたが探しているものに何らかの形で関連するページをインターネット上で探しているだけではありません。 彼はしばしばあなた自身の質問に対する答えを計算します。 さらに、通常の検索エンジンが行うように、広告の「ボーナス」の代わりに、この問題に関連する非常に興味深い事実を提供します。 リンクではなく、ページ上の事実のみ。 ただし、リンクももちろんページの最後に配られますが、通常、彼が自分で配るすべてのもので十分です。

また、必要に応じて、天気、一部の財務データ、地理、生物学、化学などのデータベースにアクセスできます。 例えばここに。 既製のリクエストとのリンク

97年から99年までのカブールの気温、気圧、その他のグラフ。

過去16年間のApple株式情報

ソ連の領土に関する地図と情報

一酸化窒素の主な特性

「...とは？」などの質問への回答に加えて、彼は入力ラインに入力された微分方程式の解を与えることもできます。 または、尋ねたグラフを描画します。 つまり、サードパーティのプログラムやプラグインなどは必要ありません-微分方程式を解いてグラフをWolfram Alphaの入力行に入力するだけで描画できます。 しかしそれでも、私はすべてが合理的であることに注意します-何か面倒なことがある場合、彼はそれを「無料」と見なすことを拒否し、複雑なタスクと速度にはまだWolfram Mathematicaが必要です。

特に、数値のシーケンスの形式で要求を行うことが可能であり、この配列の主な特性に加えて、シーケンスを続行するための仮想オプションを提供することができます（常に真とは限りません）。 上記の表のセルでどのような数字が得られたかを知るために使用されたのは、彼のこの機会でした。

数学探偵

探偵小説が嫌いな人は、 この章を飛ばし て次の 章に進む ことができます。

まず、結果のW配列の行を取得し、 Wolfram Alphaに手動で入力します。 しかし、コピー＆ペーストすることはできませんが、 Wolfram Mathematicaから直接ブラウザなしでWolfram Alphaに直接アクセスできます。 そして、興味のある情報のその部分をすぐに要求します。 ループで入力されたシーケンスの推測式を要求するコードは次のとおりです。

 For[i=1,i<=Length[W],i++, Print[i," ",W[[i]]]; Print[WolframAlpha[ToString[W[[i]]],{{"PossibleSequenceIdentification",1},{"Output"}}]]; Print[""]; ];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

残念ながら、すべてのリクエストが正常に処理されたわけではなく、理由は異なります。入力シーケンスのサイズを小さくしたり大きくしたりするのに役立ちます。 しかし、受け取った回答から、よく見ると、導入したシーケンスがa0 * 0 ^ n + a1 * 1 ^ n + a2 * 2 ^ n + a3 * 3 ^ n + ...という形式であることがわかります。 用語の数は、入力されたシーケンスの序数に等しくなります。 しかし、係数は式に線形に入力されます。つまり、線形方程式系から簡単に見つけることができます。 さらに、よく見ると、すべての項には、シーケンス番号の階乗に反比例する共通の因子があり、項は交互になっています。 したがって、これらの事実を念頭に置いて用語を検索します。 もちろん、手動ではなく、Wolfram Mathematicaでシステムを解決します。 解決するコードは次のとおりです。

 TempAr = W; CoefRes = Table[{}, {i, 1, Length[TempAr]}]; For[k = 1, k <= Length[TempAr], k++, An = Table[a[i], {i, 2, k}]; (*Conds=Table[An[[i]]>0,{i,1,Length[An]}]*) F[z_] := (Total[ Table[(((-1)^(k + 1))*(-1)^(i + 1))*i^z*An[[i - 1]], {i, 2, k}]] + (-1)^(k + 1))/((k - 1)!); Eqs = Table[F[i] == TempAr[[k]][[i]], {i, 1, Length[An]}]; Res = Solve[Eqs, An]; CoefRes[[k]] = Prepend[(An /. Res)[[1]], 1]; ue = Table[(-1)^k*(-1)^i, {i, 1, Length[CoefRes[[k]]]}]; CoefRes[[k]] = CoefRes[[k]]*ue; ]; CoefRes // Column
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

オッズは判明していますが、それらもそれほど単純ではありません。 それらの式を見つけるための同じ手順を繰り返します。 そして、ここで失望を待っています-景品モードのWolfram Alphaはこれらのシーケンスを認識できません。 さて-自分で試してみてください。

これらすべての数を素因数に分解し、少し瞑想して、結果を考えてみましょう。 このアプローチは、シーケンス式を認識するためにしばしば役立ちます。

 For[i=1,i<=Length[W],i++, Print[FactorInteger[Abs[CoefRes[[i]]]]//Column]; ]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

得られた展開を詳しく見ると、シーケンス内の各番号がそれ自身のシーケンス番号である程度分割されており、この程度はシーケンス番号の増加とともに大きくなることが明らかです。 よく見ると、この次数はシーケンス番号から2を引いたものに等しくなります。それでは、シーケンス内のすべての番号を、シーケンス番号から2を引いた数のシリアル番号に分割します。

 CoefRes2=CoefRes; For[i=1,i<=Length[CoefRes],i++, For[j=1,j<=Length[CoefRes[[i]]],j++, CoefRes2[[i]][[j]]=Abs[CoefRes[[i]][[j]]]/j^(i-2); ]; ] CoefRes2
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以前はアルゴリズムの計算結果を示しませんでした。数値の配列があり、挿入するテーブルが多すぎます。 そして、私が言ったように、数字はそれほど明確ではありません。 誰かがそれらを見たい場合は、このコードを投稿してください。 一度それを追い払って、すべてを見てください。 すぐに動作します。 今回はアルゴリズムの結果を示します。これは、数字が非常に有名だからです。

{{1}、{1,1}、{1,2,1}、{1,3,3,1}、{1,4,6,4,1}、{1,5,10,10、 5.1}、{1,6,15,20,15,6,1}、{1,7,21,35,35,21,7,1}、{1,8,28,56,70、 56,28,8,1}}、{1,9,36,84,126,126,84,36,9,1}}

ニュートンの箱とパスカルの三角形を覚えていれば、分割後に何が起こったのかは、Wolfram Alphaには反映されません。 「Tse from en po ka」と判明しました。

今では、分解されたフォーミュラからすべてのスペアパーツを集めて1つの全体に戻すことが残っています。

 FV[KK_,LL_,NN_]:=Sum[((-1)^(n+KK) n^(KK+LL))/(n! (KK-n)!),{n,1,KK}]*NN!/(NN-KK)!/(NN^(KK+LL));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

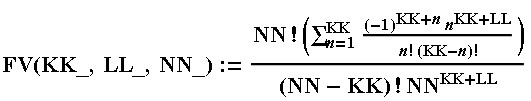
結果は分析形式で得られ、原則として、必要なものはすべて引き出すことができます。 ただし、式はやや面倒ですが、もっとコンパクトにしたいと思います。 そして、コレクションの問題がpre延しているため、確実に知るべきです。

かなり長い間、私はそれを単純化するか、文献で見つけようとしました。 その結果、ソーステーブルの行の代わりに、 Wolfram Alphaの認識のために列を送信したときに、両方を実行することが判明しました。

300年前

結果の配列Wの列をWolfram Alphaに入力すると、シーケンスは第2種のスターリング数として認識されます。 これはかなりよく知られています（結局、覚えていませんでしたが、知りませんでした）数の配列は、組み合わせ論と確率論に関するさまざまな教科書で詳しく説明されています。 スターリングの数字に詳しい人はこの章を飛ばし 次の話に進んでください 。

たとえば、 ここでスターリング数について読むことができます 。

そして、 ここでははるかに詳細ですが、しかし、英語で。 これは一般に、数学の何かに関する完全な参照情報が必要な場合、おそらく最高のサイトの1つです。

第2種のスターリング数は、N個の要素のセットをK個の部分に分割する方法の数を意味します。 たとえば、4つの要素のセット{1,2,3,4}は次のように分割できます。

それぞれ{{{a}、{b}、{c}、{d}}の1つの要素の4セットに（1つの方法しかありません）

3セットに 、1つには残りの1つに{{a、b}、{c}、d}}、{{a、c}、{b}、{d}}、{{a、d }、{b}、{c}}、{{b、c}、{a}、{d}}、{{b、d}、{a}、{c}}、{{c、d}、 {a}、{b}}（6つの方法があります）

1と3の要素の2セットに{{a}、{b、c、d}}、{{b}、{a、c、d}}、{{c}、{a、b、d}}、 {{d}、{a、b、c}}、または各2つの要素{{a、b}、{c、d}}、{{a、c}、{b、d}}、{{a 、d}、{b、c}}（7つの方法しかありません）

4つの要素の1つのセットに、つまり、何も壊すことなく。 （片道）

実際には、セットを特定の数のパーツに分割するいくつかの方法（同時にこれらのパーツの任意の構成）は、スターリング数も意味します。

スコットランドの数学者であるジェームス・スターリングは、約300年前にアイザック・ニュートンの同時代人であり、実際に定期的に連絡を取り、コミュニケーションを図り、働いていました。 彼に敬意を表して、セットをn個の部分に分割する方法の数を示す数字に名前が付けられています。

第2種のスターリング数を取得する式は次のとおりです。



しかし、Wolfram Mathematicaでは、StirlingS2関数[SS、NN]を介して利用できます。

三行

N個の要素のコレクションの問題は、3行で解決できます。 確かに、これを理解するには、かなり時間がかかりました。

1. 順次収集したコレクションのすべての要素には、受信した順序に従って番号を付けることができます。これらの数値は、要素自体の再現性に従ってグループにまとめることができます。そのようなグループの数は、第2種のスターリング数です。
2. これらのグループは、現時点でコレクションの一意の要素を配置する場所として表すことができます。このような配置のオプションの数は、K箇所の「繰り返しのない配置」N要素の数に等しくなります。したがって、K個の一意の要素を取得するためのオプションの総数は、対応するスターリング数と配置数の積に等しくなります。
3. S番目のステップでコレクションを収集する確率は、K個の一意の要素を取得する可能性の数とすべての可能な組み合わせの数の比であるN ^ Sです。
   
   部分的に収集されたコレクションではなく、収集されたコレクションに関心がある場合（既に上記で与えられた式） 、現時点での一意の要素の数は、コレクション内の要素の総数に等しいことが必要です。
   
   

したがって、N個のステップでK個の要素のコレクションを収集する確率は、StirlingS2 [N、K] * K！/ N ^ Kです。

2つのエンティティ

「：」離散確率変数の分布「および」および「離散確率変数の分布関数」の概念に精通している人は、この章を飛ばして次へ進むことができます。

サイコロを振ってみましょう。特定の数、たとえば3または5が抜ける確率は1/6です。これらのイベントの確率のグラフは、単純に水平線であるか、「棚」と呼びましょう（結局、似ています）。しかし、別の質問は非常に一般的です。特定の数以下の数、たとえば2以下の数が脱落する確率はどのくらいですか？その後、可能性のある数ごとに確率グラフを作成することもできますが、それはすでに「ラダー」の形であり、前回のように水平線ではありません。

さらに、「シェルフ」チャートでは、ポイント3.5または2.8の値はありません。単にキューブでロールアウトしないためです。この場合、非整数の数、または1未満または6を超える数については、確率をゼロと見なすか、不確実と見なすかはかなり複雑な問題ですが、ここでは単純にそれをバイパスします。 「はしご」に関しては、理解するのが難しくない重要なポイントもありますが、それを見逃して間違いを犯すのは非常に簡単です。各ステップの水平部分には「左の境界に点があります」が、「右にはありません」。ある意味では、ステップの凸角にできるだけ近づけることができますが、グラフの破損が発生する場所のラダーの関数の値は、上（次）のステップの値に等しくなります。例えばキューブで2以下の数を取得する確率は1 / 3、2.5以下の数を取得する確率も1 / 3、2.999999999以下の数を取得する確率も1/3ですが、3以下を取得する確率は既に1 / 2。





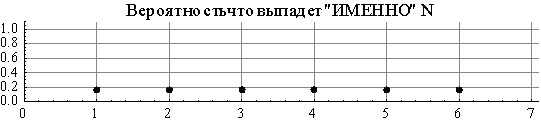
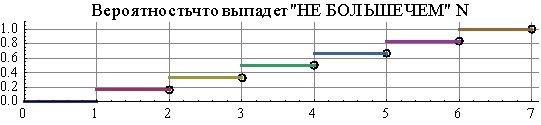
キューブは同じです。あちらこちらで確率グラフを作成しているようです。しかし、それらは異なります。非常に多くの場合、ターバーを勉強するとき、これらの2つのエンティティの混乱のために問題が正確に発生します。これは、部分的には名前が非常に似ているためです。そして、なぜ彼らが2人で導入されたのかが完全には明らかではないという事実により、1人でうまくいくことができました。特に、「はしご」は当初、情報量が少なく無意味であると認識されています。

これらの2つのエンティティは、次のように呼び出されます。

1. 私たちが「SHAFT」と呼んだもの：「離散確率変数の分布則」、あるいは単に（法則という言葉なしで）「離散確率変数の分布」、または「確率分布」または「分布表」よりも短い。
2. 「LESENKA」と呼ばれるもの：「離散確率変数の分布関数」。

さて、誰かが「機能」と「法律」の顕著な違いをはっきりと明確に理解したら、クッキーを食べてください。会話中に、「配布機能」が単に「配布」に単純化され、それだけで違いがまったくない場合は、特に悪いことです。重要なことを誤解しているのは残念です。結局のところ、言語的な妨害のためであり、あなたが意味を理解できないからではありません。ここで教えるTerverはまったく問題を認識しておらず、学生は苦しんでいます。

「棚」と「はしご」が常にそのように得られるわけではないことは明らかです。たとえば、キュ​​ーブの値についてはグラフを描画せず、人々の成長については、グラフはもはや棚ではなく（人々はすべて同じ高さではありません）、むしろ何らかの「ドーム」になります。その最大値はおそらく160cmです。しかし、200cmと140cmの成長の確率はずっと低くなります。しかし、はしごは、個別の場合では、ほとんどの場合「はしご」です（非実用的であるため、現在は扱いにくいまれな場合を考慮していません）が、それでも、これは通常かなり短いはしごです。

これらのエンティティは、名前を付けずに抽象的に頭で認識するのが最善です。しかし、会話では、抽象的なものではなく具体的​​なものを適用する必要があります。そのため、私は通常（もちろん、Terverの人々は私を生き埋めにしますが）次の概念を使用します。 「はしご」の本質を示す「積分」、および「棚」の本質を示す「密度」。このような定義の意味はかなり優れています。 3以下の数がキューブに表示される確率は、1が抜ける、または2が抜ける、または3の確率の合計を意味します。つまり、3未満のすべての可能なオプションの確率の合計は、「積分」-「ラダー」グラフの値を提供しますポイント3で、積分は実際には合計であり、したがって私が使用する表記法です。密度とは、単純に大まかに言うと、ボリューム全体の1つの小さな部分の質量です。場合に厳密に固定された1つの値が抜ける確率について話すときは、可能性のある値のセット全体から分離し、彼だけが話し、それについて話します。したがって、2番目の表記が使用されます。

ここで疑問が残ります。なぜ「積分」確率のグラフとしてそのようなエンティティを個別に導入する必要があるのですか。キューブの場合、これは実際にはあまり明確ではありません。別の例を試してみましょう。 100人の人がいて、それぞれが給料を受け取っているとします。給料は勤続年数、仕事のさまざまなメリット、資格などに依存します。この状況では、すべての給料は少なくともわずかに異なります。 1つは30トンです。別の32人、5人、それぞれ35人、36人、そして正確に34人は誰も獲得できません。ここで、「密度」確率グラフがあることを想像してください。つまり、正確に32t.rになる確率は1/100であり、34tになる確率グラフであると言えます。それをまったく理解していません（100人の従業員がいて、32t.rを獲得するのは1人だけで、34を獲得する人はいません）。さて、32t.rの1/100の確率の知識から、または34t.rのデータがまったくないという事実から、どのような有用な結論を引き出すことができますか？基本的になし。ここで、「積分」確率のグラフがあると想像してください。それによると、あなたは30ルーブル未満になる確率は何であるかを言うことができます、そして、これはいくらか具体的なパーセンテージになります。そして、例えば10t.r未満の確率がゼロであることが判明した場合、これは誰も10t.r未満にならないことを意味し、これは給与が34,234rであるという事実よりもはるかに有益です。 20,000誰も。これは、誰も10 trを下回らないことを意味します。これは、給与が34,234 pであるという事実よりもはるかに有益です。 20,000誰も。これは、誰も10 trを下回らないことを意味します。これは、給与が34,234 pであるという事実よりもはるかに有益です。 20,000誰も。

もちろん、「何かより大きく、何かより小さい確率」などのグラフを作成することもできます。その場合、合計は指定された値よりも小さい値ではなく、ある値から別の値になります。しかし、これらはすでに具体的な例であり、特定のケースごとに異なります。しかし、「確率積分」と「確率密度」のグラフは誰もが広く使用しているため、2つの別個の重要なエンティティに区別されます。

これら2つのエンティティの意味を理解し、それらの使用の適切性を理解することは、受け取った収集問題の公式と、数値モデリングで得たデータを理解するために必要です。これは、ステップ数に応じて、特定のステップ数のコレクションを収集する確率のグラフです。また、モデリングによって得られたデータがどのように見えるかについても思い出します。チャートは大きく異なります。





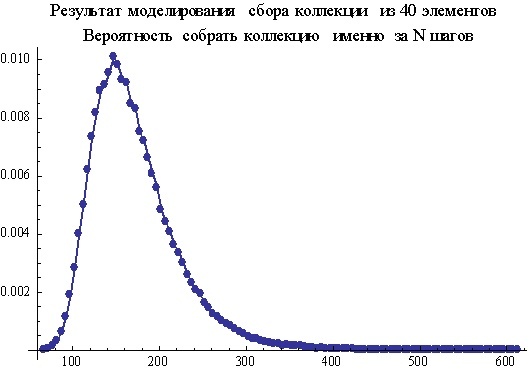
違いは、モデリングによって得られたグラフが「確率密度」であり、式に従って「積分確率」であるという事実によって説明されます。この式は、N個のステップでコレクションを組み立てる確率値を提供します。正確にはNではありません！しかし、単純に-Nの場合です。つまり、コレクションをほぼ即座に収集でき、Nステップを実行するまで要素の繰り返しのみを取得し、そのような奇妙なケースを考慮に入れました。混乱や誤解を避けるために、「N個以下のステップでコレクションを収集する確率」または「... N個以下のステップで収集する」という式について言う方が正しいです。また、モデリングによって得られたグラフについて、「コレクションを取得する確率はN番目のステップにある」、つまり、コレクションが（N-1）番目にまだアセンブルされていないが、N番目のステップにアセンブルされている場合、言う必要があります。

「確率積分」の式から「確率密度」の式を取得するには、確率からN以下のステップからコレクションを収集し、（N-1）以下のステップでコレクションを収集する確率を減算する必要があります。得られる差は、N番目のステップでコレクションを収集する確率であり、それ以前ではありません。したがって、N番目のステップでK個の要素のコレクションを収集する確率は、StirlingS2 [N、K] * K！/ K ^ N- StirlingS2 [N-1、K] * K！/ K ^（N-1）

この式は削減できることに注意してください。実際には、1つの要素のみを収集することが残っている場合、これは1つの独自の方法でのみ実行できます。これは、N番目のステップでコレクションを収集する確率は、N番目のステップで可能なすべての要素セットの総数に対する（N -1）ステップで収集する可能性の数の比率に等しいことを意味します。その結果、式はStirlingS2 [N-1、K-1] * K！/ K ^ N の形式に縮小されます。

次のグラフでは、コレクションを収集するための式がN番目のステップで実線で示され、赤い点がシミュレーション結果を示します。あなたが見ることができるように、彼らはかなり良いマッチです。

医師の平均患者体温と平均給与

これから説明することは、日常生活で知るのに非常に重要で有用です。平均、期待値、および中央値の概念に精通している人は、この章を飛ばして次へ進むことができます。

コレクションを組み立てるのにいくつの「平均的な」ステップが必要なのでしょうか？単純で自然な、よくある質問のようですが、1つの問題があります。 「平均」について話すとき、私たちが正確に知りたいことを明確にする必要があります。

この状況を想像してください。売り手は、毎日1、2、3など、最大6千ルーブルの利益を上げています。まるで彼の日々の利益は、サイコロに落ちた数字に依存しているように。そして、このモードでの1か月の作業の後、彼は平均を計算することにしました。彼は30日間すべての利益額を計算し、日数で割った。結果の数値は、30日間すべての利益の算術平均です。数値は非常に有益ですが、1つの重大な欠点、欠点があります。実際には、発生したイベントの一部に関するデータが既にある場合にのみ計算できます。翌月の利益の平均値を知りたい場合、現時点では算術平均を計算する方法を使用して見つけることはできません-翌月のデータがないため、折りたたんで分割することができます。しかし、来月の彼の仕事は同じようであり、災害は予想されず、商品の供給の中断や需要の低下も予想されていません。売り手は、ランダム変数のプロパティが来月変更されないことを期待しています。そうだとすれば、1か月に計算できる平均値も先月に取得した平均値とあまり変わらないと想定できます。 「強くない」が何を意味するのかという質問は、今はスキップします。それはかなり複雑で、今は緊急ではありません。来月のおおよその平均利益を予測する方法を見つけてみましょう。商品の供給の中断と需要の減少、彼はまた期待していません。売り手は、ランダム変数のプロパティが来月変更されないことを期待しています。そうだとすれば、1か月に計算できる平均値も先月に取得した平均値とあまり変わらないと想定できます。 「強くない」が何を意味するのかという質問は、今はスキップします。それはかなり複雑で、今は緊急ではありません。来月のおおよその平均利益を予測する方法を見つけてみましょう。商品の供給の中断と需要の減少、彼はまた期待していません。売り手は、ランダム変数のプロパティが来月変更されないことを期待しています。そうだとすれば、1か月に計算できる平均値も先月に取得した平均値とあまり変わらないと想定できます。 「強くない」が何を意味するのかという質問は、今はスキップします。それはかなり複雑で、今は緊急ではありません。来月のおおよその平均利益を予測する方法を見つけてみましょう。これは「強くない」ことを意味します。ここではスキップします。かなり複雑で関連性があまりありません。来月のおおよその平均利益を予測する方法を見つけてみましょう。これは「強くない」ことを意味します。ここではスキップします。かなり複雑で関連性があまりありません。来月のおおよその平均利益を予測する方法を見つけてみましょう。

算術平均を考慮すると、観測中にランダムな値（給与）で得られたすべての値を合計し、総数で除算しました。このプロセス全体を詳しく見てみましょう。受信したすべてのデータをテーブルに書きましょう。



ユニットはk1回、デュースはk2回ドロップしました。 （数千単位でカウントしましたが、簡潔にするためにゼロを書きません）。その後、キューブに落ちたすべてのものの合計を見つけました（まあ、またはそれが何であれ-私たちは毎日獲得しました）。この合計の被加数は1 2 3 4 5 6の数字であり、それぞれがそれぞれk1 k2 k3 k4 k5 k6回でした。これは、この合計がS = k1 * 1 + k2 * 3 + k3 * 3 + k4 * 4 + k5 * 5 + k6 * 6。この合計の項の総数は、N = k1 + k2 + k3 + k4 + k5 + k6でした。実際、k [x]はそれぞれの値が何回低下したかを示し、合計で6回あります。その後、SをNで除算します。これはS / N = 1 *（k1 / N）+ 2 *（k2 / N）+ 3 *（k3 / N）+ 4 *（k4 / N）+ 5 *（k5 / N）+ 6 *（k6 / N）。しかし、詳しく見ると、k1 / Nはそれぞれユニットが脱落する確率に非常によく似ています。k2/ Nは2が脱落する確率などです。イベントの発生数をイベントの総数に分割します。しかし、乱数が抜けるプロセス、乱数の分布の法則は先月変更されず、次の年に変更される予定もなかったようです。これは、タイプ（k1 / N）の関係は時間に依存せず、ランダム変数のプロパティにのみ依存することを意味します。そして、いつの日か実験的に得られた観測からそれらを取得できれば（もちろん、計算されて分割されます）、将来的にそれらを使用することができます。さらに、S / Nはランダム変数のプロパティのみに依存し、時間に依存しないようになりましたが、現在ではWHAT_ DROPPED * PROBABILITY_DECLINED_TOGO_WHERE_DEPENDEDという形式の用語のみが残っていることがわかりました。配給法自体は先月ランダムに変更されておらず、次の月に変更される予定もなかったようです。これは、タイプ（k1 / N）の関係は時間に依存せず、ランダム変数のプロパティにのみ依存することを意味します。そして、いつの日か実験的に得られた観測からそれらを取得できれば（もちろん、計算されて分割されます）、将来的にそれらを使用することができます。さらに、S / Nはランダム変数のプロパティのみに依存し、時間に依存しないようになりましたが、現在ではWHAT_ DROPPED * PROBABILITY_DECLINED_TOGO_WHERE_DEPENDEDという形式の用語のみが残っていることがわかりました。配給法自体は先月ランダムに変更されておらず、次の月に変更される予定もなかったようです。これは、タイプ（k1 / N）の関係は時間に依存せず、ランダム変数のプロパティにのみ依存することを意味します。そして、いつの日か実験的に得られた観測からそれらを取得できれば（もちろん、計算されて分割されます）、将来的にそれらを使用することができます。さらに、S / Nはランダム変数のプロパティのみに依存し、時間に依存しないようになりましたが、現在ではWHAT_ DROPPED * PROBABILITY_DECLINED_TOGO_WHERE_DEPENDEDという形式の用語のみが残っていることがわかりました。（そして、もちろん、カウントと分割）、将来的に使用できます。さらに、S / Nはランダム変数のプロパティのみに依存し、時間に依存しないようになりましたが、現在ではWHAT_ DROPPED * PROBABILITY_DECLINED_TOGO_WHERE_DEPENDEDという形式の用語のみが残っていることがわかりました。（そして、もちろん、カウントと分割）、将来的に使用できます。さらに、S / Nはランダム変数のプロパティのみに依存し、時間に依存しないようになりましたが、現在ではWHAT_ DROPPED * PROBABILITY_DECLINED_TOGO_WHERE_DEPENDEDという形式の用語のみが残っていることがわかりました。

たくさんの言葉を書かないように、可能なすべてのオプションTOGETHER_THINGS_DROPEDをX（i）で示します。 （「Xx-5番目、6番目、ento、kato、itoの意味）」合計でX（i）6個があります。これは、ランダム変数が6つの値のうちの1つしか受け取らないためです。さらに、X（1）= 1、X（2）= 2などです。そして、WHAT_のLOSS_SIDE_の確率は、P（i）から抜け落ちました。そして、ランダム変数X（i）の各値は、P（i）の発生確率に対応しています。このような指定では、S / N値をより簡単に書くことができますS / N = SumAll [P（i）* X（i）]（すべてのi）。用語は6つしかありません。わかりやすくするために記述します。

S / N = P（1）* X（1）+ P（2）* X（2）+ P（3）* X（3）+ P（4）* X（4）+ P（5）* X （5）+ P（6）* X（6）

だからここ。値SumAll [P（i）* X（i）]（すべてのi）は数学的な期待値と呼ばれます。これはまだ受信されていないという意味で、数学的分析の後に予想される、ランダム変数の平均値。キューブの場合、期待値は1 *（1/6）+ 2 *（1/6）+ 3 *（1/6）+ 4 *（1/6）+ 5 *（1/6）+ 6 *（1 /6)=21/6=3.5。整数面のみを持つキューブの場合、この事実に最初に遭遇したとき3.5が何であるかを理解するのは通常簡単ではありません-3.5面はありません！マットの期待値は、ランダム変数の値の1つと同じである必要はありません。 1日あたり平均3500ルーブルの利益を得ている売り手にとっては、すべてが明確です。

今度は、キューブを10回転がし、数字の6が10回すべて転がると想像してください。算術平均値を計算すると、6になります（明らかに）。そして、私たちはそのマットを言います。期待値3.5、および正確には3.5である必要がありますが6ではありません。ここで、観測データから得られた算術平均値が期待値と異なる場合があります。実際、期待は期待される平均であり、実際には時々起こることはありません。現実に近いが、実際の値に等しくない予想されるものは、直接確実です。しかし、定理（「多数の法則」）があります。これは、サイコロを振る回数が増えるほど、算術平均を計算する回数が増えるほど、期待値と平均値の差が小さくなることを意味します。そして与えられたほとんどの場合、長時間の実験を行う機会はなく、一般に、実験なしで平均的に何が起こるかを予測したいので、何らかの評価として、数学的予測を使用することで満足することができます。エラー。

一方で、いくつかのランダムなプロセスを説明する場合、平均値は非常に有益ですが、時々、平均値は単に無意味で非論理的であり、その使用は常識と現実に反しています。そして、ここでのポイントは、最も平均的な値ではなく、それを検討する人々の健全性です。

ある病院の主任医師は、レポートに次の文言を書くのが大好きでした。「患者の平均体温は36.6度で、これは標準と完全に一致しています。」彼は嘘をつきませんでしたが、正直にすべての患者の体温、40度の発熱がある人、死亡して室温まで冷やした人の数を数えました。平均して、36.6が得られました。患者の体温分布のグラフを描くことで、より多くの情報を得られるでしょう。それを見て、何人の人がまだ生きており、何人の人が通常よりも体温が高いかを推定することができます。もちろん、例は逸話ですが、驚くべきことですが、平均値を考慮するのは無意味な場合があります。

平均値を使用するもう1つの例は、有害で誤解を招くほどには意味がありません。多くの場合、メディアでは、そのような業界の平均給与に関する言及を聞くことができます。通常、給与の分布図を表示することはありません。印刷するのが面倒な人も、エキストラを依頼するのが面倒な人もいます。そして、あなたに見せます（もちろん発明されましたが、現実に非常に近いです）。



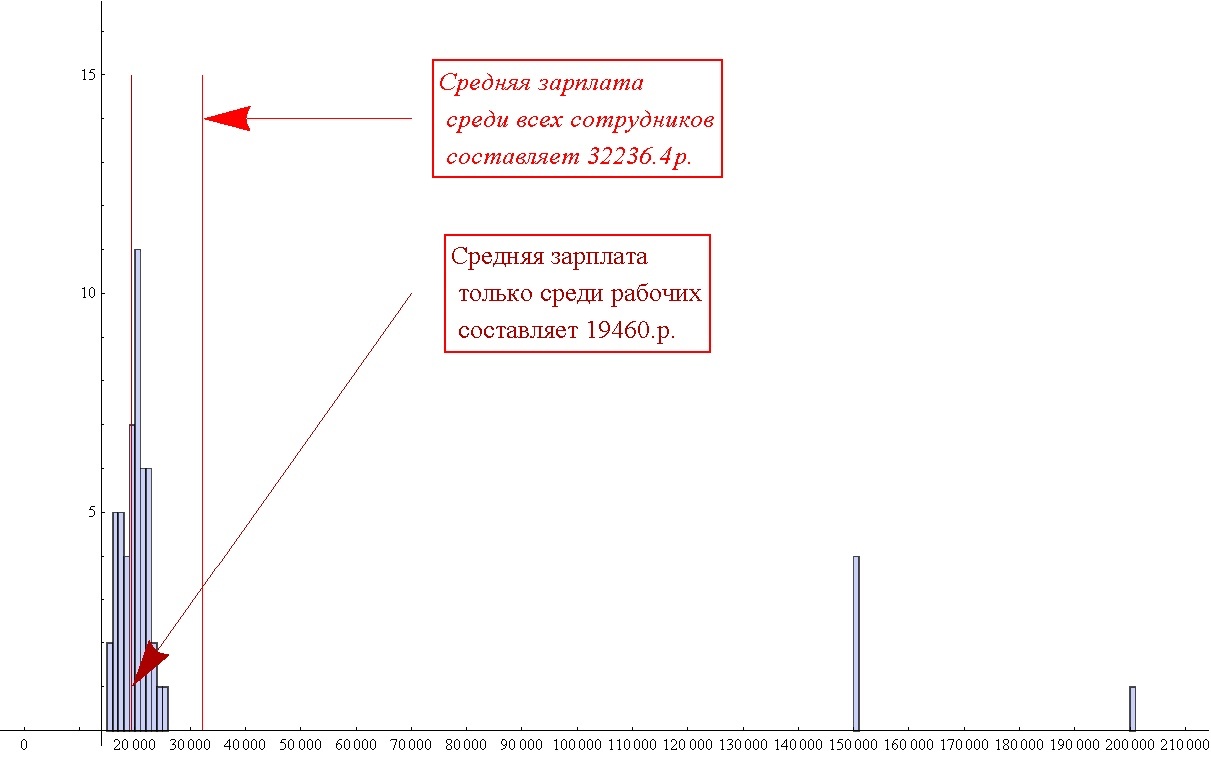
分布は次のとおりです。50人の労働者が約20t.rを受け取ります。チーフ200、および150t.rの彼の4つの代理。メディアは、この企業の平均給与は32,236ルーブル、40コペックであると正直に書いています。もちろん、労働者は、平均してそのような給料を受け取っていると聞いて非常に驚いています。平均値はそれだけです。それだけが、ほとんどの従業員の給与の1.5倍です。そして今、誰も誰もだましていない。一方、スケジュールを表示する方が正確ですが、はるかに長くなります。また、グラフは非常に複雑であるため、誰もがグラフに描かれているものをすぐに理解できるわけではありません。はい、コレクションの問題でさえ、すべての人がグラフを作成したい、またはそれ以上にグラフを作成したいとは思わないでしょう。むしろ、彼らはコレクションを収集するために非常に「平均的な」数のアイテムを聞きたいと思うでしょう。1つの番号は、配布よりも簡単に実現できます。

もう1つの「数」がありますが、これは簡潔ですが、時には予想よりも分配の法則をより情報的に説明するものです。これは中央値と呼ばれます（いいえ、これは三角形と同じ中央値ではなく、名前が似ているだけです）。

給与に関する前述の例では、そのような質問をすることができます-企業従業員の50％が受け取る金額以下です。この質問に対する答えとなるまさにその量が中央値と呼ばれます。ただし、中央値は常に存在するとは限りませんが、それに最も近い意味があります。このニュアンスは特別な役割を果たしていません。50％の値を厳密に取得することはできませんが、最も近いものは常に可能です。この例では、従業員の61.8％が21トン以下の給与を受け取っていると言えます。さらに、従業員の89％が25t.r以下の給与を受け取っていると言えます。この数値は中央値ではなく、分位数（89％）と呼ばれます。実際には、中央値も分位数ですが、頻繁に使用され、正確に50％であるため、独自の名前を付けました。同意します。「従業員の89％は25 tr以下の給与しか受け取りません。「平均給与32 tr」よりもはるかに有益な音。理想的には、もちろん、これを言った方がいいですし、長すぎたり言ったりすることは難しくありません。確かに、聞き手は、彼らが言われたことを理解しないことに慣れていないかもしれません。

特に思慮深い人々は、おそらくどのような50％を採用するかを尋ねます。上司と代理が同じ50％を入力すると、再びナンセンスになります。はい、動作しますので、まずすべてを昇順でソートし、最小から最大までパーセンテージをカウントする必要があります。法律と分布関数の説明でこの点を見逃しましたが、それらは常に昇順で正確に構築されます。

実際には、変位値、または中央値でさえ、計算するのは非常に困難です。中央値については、F（x）= 0.5の形式の方程式を解く必要があり、逆関数は各分布から計算が容易であり、常に存在するとは限らないため、最も近いものを探す必要があります。その結果、方程式ではなく不平等が得られ、その後異なるケース（異なる企業または月）について定量化する場合、書き留めて比較する必要があり、異なるパーセンテージからそれらを取得する必要があり、これは不便です。

ところで、収集の問題については、分位数を分析的に計算する方法はわかりませんが、数値解で取得します。

直接登らない場合は横に行きます

コレクションの問題では、コレクションを収集する前に、平均的なコレクターがステップ（チューインガムを開く）を行う数を知りたいと思います。数式を使用して数式を使用し、以前に取得した確率分布の法則（「密度」）を使用できます。しかし、私はそのような量を計算できなかったと言わなければなりません-式はまだ非常に複雑であり、それを最小化する方法は明確ではありません。

「額」を解決することは不可能であるため、少なくともなんとかしてみます。期待のプロパティの1つは、これに役立ちます。私はそれを証明せずに提供します。これは短くて複雑ではなく、Terverの教科書で見つけることができます。

2つの独立したランダム変数の合計からのマット期待値は、これらの各変数からの期待マットの合計に等しくなります。

たとえば、キュ​​ーブにはマットがあります。マットとは何ですか？同時に投げられた2つのサイコロの数字の合計に対する期待。上記のルールに従って、答え7が得られます。

ある時点で、K個の一意の要素があり、コレクションに合計N個の要素があるとします。別の一意の要素を取得する確率は（NK）/ Nであり、別の繰り返しを取得する確率は等しくなります。 K / Nそのような状況では、正確にMステップで一意の要素を取得する確率は（NK）/ N *（K / N）^（M-1）です。つまり、これは繰り返しを受信する前であれば、一意の要素を取得する確率です。新しい一意の要素を取得するために必要なステップの平均値を計算するには、予測式を使用します。ちなみに、手動で計算することは難しくありませんが、ここに数学で計算するためのコードがあります。

 Sum[i*(nk)/n*(k/n)^(i-1),{i,1,Infinity},Assumptions->{k/n<1}]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その結果、すでにK個の一意の要素があった場合、平均してN /（NK）ステップ（チューインガムを開く）で新しい要素を取得する必要があります。

コレクション全体を収集するために受信した要素（すべてオープンチューインガム）の平均値は、N /（NK）に等しい一意の要素を取得する間に行われたステップ数の平均値の合計に等しくなります。たとえば、最初の一意の要素を取得するにはN /（N-0）= 1ステップ（チューインガムを開く）、最後の一意の要素を取得するにはN /（N-（N-1））= Nステップが必要です、最後から2番目のN /（N-（N-2））= N / 2ステップ、最後から2番目のN /（N-（N-3））= N / 3ステップなど。結果として、ここで合計が得られます。この種のN + N / 2 + N / 3 + N / 4 + ... + N /（N-2）+ N /（N-1）+ N / Nより簡単な形式で記述できます：N *（1 + 1/2 + 1/3 + 1/4 + ... + 1 / N）。

これは、コレクションを組み立てるためにアイテムを取得するのに平均してどれくらい必要かという質問に対する答えです。

何らかのウィキ

ロシアのウィキペディアに入ろうとさえしないでください。公式、定理、およびロシアのウィキペディアで少し科学的なものに関するすべては、見るのに有害です！記事は少なく、記事から何かを学ぶのは現実的ではないような言語で書かれています。非常に深刻な本の中から最も自明でない文字を使用して書かれた定義の破片を持っているため、ウィキペディアの記事の著者は、問題の本質または少なくとも使用されている表記の意味を説明しようとせずに単にコピーしているようです。重大なセマンティックエラーが発生することはまれです。

ほとんどのユーザーはすでにすべてがウィキペディアで非常に単純に書かれているという意見を持っています。もしそうなら、ウィキペディアで明確でない場合、質問は非常に複雑であり、それを忘れた方が良いです。ある種の反教科書は簡単です-興味と啓発の代わりに、それは完全に学習から遠ざかるか、誤解を招きます。

ところで、この記事のトピックに関連する質問を検索する過程で、James Stirling専用のウィキペディアページに入りました。

彼は300年前に住んでいたので、ページに添付された画像は、画像の質と描かれた男性の外観のために私を疑わせました。他の言語のジェームズ・スターリングのページでは、この画像はどこにもありませんでした。ほとんどの場合、そこにはありませんでしたが、スロバキア語、アルメニア語、ハンガリー語、ヘブライ語、ロシア語のページにありました。画像へのリンクは非常におもしろい結果を与えました。

これは、20世紀の哲学者グスタフバーグマンの写真です。少なくともアイオワ大学の公式ウェブサイトでこれが述べられています。

ウィキペディアには本当に優れた信頼できる記事が含まれていましたが、すべてが変わります。そして、ロシアのウィキペディアはさらに悪化し続けています。

しかし、公平に言うと、英語版ウィキペディアのページはよく書かれていることが多いことに注意してください。

結果

第2種のスターリング数を使用して記述できる数式は、2つのバージョンで記述されます。

Wolfram Mathematicaでは文字NとKが予約されているため、NNという形式の表記が使用されます。これは、2文字の積ではなく、1文字を意味します。

すべての式で、NNはコレクション内の要素の数、KK-一意の要素の数、LL-繰り返しを示します。 MMが発生することもあります-これは、現時点で利用可能なすべての要素（コレクターが現在持っているもの）を意味します。はい、MM = KK + LL。この表記法の導入は冗長に思えますが、式の説明では便利です。

いくつかの式は、StirlingS2を使用する一般的な2つのバージョンで提供されます。ただし、これら2つのオプションは完全に同一です。

1. , .
   
   , MM KK LL . ( = KK+LL)
   
   Wolfram Mathematica
   
   

    FV[KK_,LL_,NN_]:=Sum[((-1)^(n+KK) n^(KK+LL))/(n! (KK-n)!),{n,1,KK}]*NN!/(NN-KK)!/(NN^(KK+LL)); FVs2[KK_,LL_,NN_]:=StirlingS2[KK+LL,KK]*NN!/(NN-KK)!/(NN^(KK+LL));
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
   
   
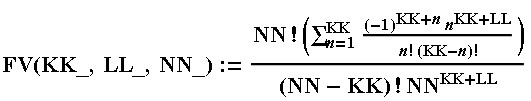
2. , MM- «» KK LL . ( = KK+LL)
   
   Wolfram Mathematica
   
   

    TV[KK_,LL_,NN_]:=Sum[((-1)^(n+KK-1) n^(KK-1+LL))/(n! (KK-1-n)!),{n,1,KK-1}]*NN!/(NN-KK+1)!/(NN^(KK+LL)); TVs2[KK_,LL_,NN_]:=StirlingS2[KK+LL-1,KK-1]*NN!/(NN-KK+1)!/(NN^(KK+LL));
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
3. . , , SS . ( , .)
   
   Wolfram Mathematica
   
   

    FCompleteNN[SS_,NN_]:=If[SS<NN,0,Sum[((-1)^(n+NN) n^SS)/(n! (NN-n)!),{n,1,NN}]*NN!/(NN^SS)]; FCompleteNNs2[SS_,NN_]:=If[SS<NN,0,StirlingS2[SS,NN]*NN!/(NN^SS)];
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
   
   重要！ , Wolfram Mathematia , Wolfram Alpha . , N .
   
   
4. , , SS . ( , SS- ).
   
   Wolfram Mathematica
   
   

    TCompleteNN[SS_,NN_]:=If[SS<NN,0,Sum[((-1)^(n+NN-1) n^(SS-1))/(n! (NN-1-n)!),{n,1,NN-1}]*NN!/(NN^SS)]; TCompleteNNs2[SS_,NN_]:=If[SS<NN,0,StirlingS2[SS-1,NN-1]*NN!/(NN^SS)];
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
5. :
   
   , , .
   
   Wolfram Mathematica
   
   

    MeanFCompleteNN[NN_]:=Sum[NN*(1/k),{k,1,NN}]; MaxTCompleteNN[NN_]:= Module[{SSm=IntegerPart[MeanFCompleteNN[NN]-(3+0.5777490650280465*NN)] ,NNm=NN,TVOld=0,TVNew=0}, If[SSm<NNm,SSm=NNm]; TVOld=TV[NNm,SSm-NNm,NNm]; TVNew=TV[NNm,SSm-NNm+1,NNm]; While[(TVNew-TVOld)>0, SSm=SSm+1; TVOld=TVNew; TVNew=TV[NNm,SSm-NNm+1,NNm]; ]; SSm ]; MedianaFCompleteNN[NN_]:= Module[{SSm=IntegerPart[MeanFCompleteNN[NN]-(3+0.2116249898999874*NN)],NNm=NN}, If[SSm<NNm,SSm=NNm]; While[FV[NNm,SSm+1-NNm,NNm]<0.5, SSm=SSm+1; ]; SSm ];
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
6. ( ±2 1000)
   
   ,
   
   
   
   
7. , , 50%.
   
   
   
   

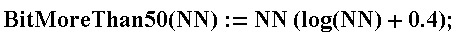
西部の本土の手の届かない場所にあるゲームArcheAgeでは、「Traveller's Bag」を見つけることができます。これには、とりわけEricの日記のページが含まれます。80個のユニークなページをすべて収集すると、それらから完全な日記を復元し、タイトルとして報酬を得ることができます。これにより、所有者はドロップしたときに受けるダメージが少なくなります。得られた式を使用すると、プレイヤーは日記全体を独立して収集するために、平均で397個のバッグを見つける必要があると言えます。また、400個のバッグを取り上げたため、すべてのページを収集する確率は58.7％であると言えます。

誕生日とカビの銀行

時には、あるいは場合によっては頻繁に、人々は質問の数学的分析に時間をかけるのではなく、直感にかなり無謀に依存します。 2つの質問に答えることをお勧めします。あなたの直観に対するあなたの「内なる感情」にのみ頼って、彼らに答えてみてください。

最初の質問はこれです。クラスには23人の生徒がいます。少なくとも1人が同じ誕生日になる可能性はどのくらいですか？

2番目の質問はカビです。 1つのカビ細胞が栄養溶液とともに瓶に飛び込み、時間tが2で除算されました。その後、これら2つのセルはそれぞれ、時間t後に再び共有されます。 1時間後、缶は正確に半分のカビ細胞で満たされました。銀行は何時に満杯になりますか？

待って、読んでいないで、少なくともいくつかの答えを出そうとしてください。正しく答えれば、1000ルーブルを受け取り、正しくなければ100ルーブルを受け取ります。1分以内に答えなければ、何も得られません。これは単なるインセンティブのためですが、タスクは「考える必要がある」というトリックだと思います。そして、人々は通常、トリックを疑うときだけ慎重に分析を始めます。もちろん、これは良いことです。しかし、他の場合でも直感に頼らない方がいいでしょう。しかし、今ではあなたの直感のテストがまさにそれです。答えましたか？

1行の誕生日に関する質問に対する回答は、コレクションについて以前に導出された式から取得されます。 1年のすべての日はコレクション内の要素の数、23人は現在の要素の数、繰り返しは0です。少なくとも2人が同じ誕生日を持っている確率は、1から誕生日が一致しない確率を引いたものに等しくなります。誰も。ライナーとチューインガムに関しては、23個のユニークな要素、0回の繰り返し、365個の要素がコレクション全体を含むことを意味します。 23人中少なくとも2人の誕生日が一致する確率は

1-FV [23,0,365] = 0.507297 = 約 50％です

つまり、クラスでは、誰かの誕生日がかなり高い確率で一致しました。ちなみに、クラスでは、クラスメートの一人と一致したのは私の誕生日でした。実践が示すように、ほとんどの人にとって、活動の種類に関係なく、このような高い確率はまったく予想外です。たとえば、答えを見つけてとても驚きました。しかし真実は、コレクションに関する公式がここで非常にうまく機能することを嬉しく思いました。

カビについての質問への答えは、あなた自身がそれを見つけることをお勧めします。

結論

直感、興奮、感情、これらすべてが生きることがなければ退屈です。しかし、それにもかかわらず、これらは人間の最も弱い場所です。そして、詐欺師、広告主、PRマネージャー、マーケティング担当者、その他多くの人々が積極的にbe打しているのは、まさにこれらの弱点です。受け取った情報と自分の計画の数学的分析は、優れた防御または強力な武器のいずれかです。それをどのように適用するかはあなたとあなたの良心次第です。主なことは、店舗に行ったり、ニュースを読んだり、コンピューターゲーム中に戦術や戦略を計画したりといった、あらゆる状況で受信した情報の数学的分析の習慣を身に付けることです。特にゲーム中。