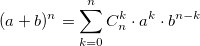C（C ++）およびPythonでの二項係数の計算

組み合わせ論の問題を解くとき、しばしば二項係数を計算する必要があります。 ニュートン二項式 分解 二項係数も使用します。 それらを計算するには、階乗による二項係数を表す式を使用できます。 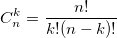または、繰り返し式を使用します。 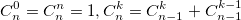ニュートンの二項式と回帰式から、二項係数は整数であることが明らかです。 この例では、単純な問題を解決する場合でも、熊手を踏むことができることを示したいと思いました。

計算手順の記述に進む前に、いわゆるパスカルの三角形について考えてください。

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

または彼は、しかし、わずかに異なる形です。 行の左側の列の値n 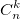k = 0..nの場合

  n   0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1 9 1 9 36 84 126 126 84 36 9 1 10 1 10 45 120 210 252 210 120 45 10 1 11 1 11 55 165 330 462 462 330 165 55 11 1 12 1 12 66 220 495 792 924 792 495 220 66 12 1 13 1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1 14 1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 15 1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1 16 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

値の繰り返し式に完全に従って 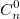1に等しく、任意の数は、その上にある数と「その上+左へのステップ」の数の合計に等しくなります。 たとえば、7行目の数値は21、6行目の数値15と6：21 = 15 + 6です。 また、行の値は行の中央に対して対称であることがわかります。 。 これは、aとbに対するニュートンの二項の対称性であり、階乗の式で見ることができます。

二項係数については以下 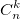また、C（n、k）表現を使用します（入力が簡単で、画像式をどこにでも挿入することはできません。

階乗公式による二項係数の計算

二項係数は非負なので、計算では符号なしの型を使用します。

 //   n unsigned fakt(int n) { unsigned r; for (r=1;n>0;--n) r*=n; return r; } //  C(n,k) unsinged bci(int n,int k) { return fakt(n)/(fakt(k)*fakt(nk)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

関数bci（10,4）を呼び出します-210を返し、これは係数C（10,4）の正しい値です。 計算の問題は解決されましたか？ はい、解決しました。 しかし、そうではありません。 質問には答えませんでした。bci関数はn、kのどの最大値で正しく機能しますか？ 答えを探し始める前に、使用しているunsigned int型は4バイトで、最大値は2 ³² -1 = 4'294'967'295であることに同意します。 n、k C（n、k）がそれを超えるものは何ですか？ パスカルの三角形に戻ります。 行の中央で最大値に達することがわかります。 k = n / 2の場合 nが偶数の場合、最大値は1つあり、nが奇数の場合は2つあります。 C（34.17）の正確な値は2333606220であり、C（35.17）の正確な値は4537567650です。 既に最大の符号なし整数より大きい。

テスト手順を作成します

 void test() { for (n=10;n<=35;++n) printf("%u %u",n,bci(n,n/2); //  C++   cout<<n<<" "<<bci(n,n/2)<<endl; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次の行の値は、前の行の値の約2倍でなければなりません。 したがって、最後に正しく計算された係数（上記の三角形を参照）はC（12.6）です。unsignedintは40億を保持しますが、1000未満の値は正しく計算されます。 全体のポイントは、bciプロシージャ、より正確には最初に分子で大きな数を計算し、それを分母で大きな数に分割する行にあります。 C（13.6）を計算するには、13！が最初に計算され、この数は60億を超え、unsigned intに適合しません。

計算を最適化する方法 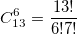？ 非常に簡単：13を明らかにする！ 分子と分母を7減らします！ 結果は 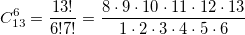。 この式を使用して計算をプログラムします

 unsigned bci(int n,int k) { if (k>n/2) k=nk; //    k, nk..    C(n,k)=C(n,nk) if (k==1) return n; if (k==0) return 1; unsigned r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return r; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

：



明らかに、Cの計算中にエラーが発生しました（31.15）。 理由は明らかです-同じオーバーフロー。 最初に31を乗算します（op-pa-オーバーフロー、次に15で除算）。 しかし、再帰式を使用するとどうなりますか？ 追加のみがあり、オーバーフローはありません。

さて、試してください：

 unsigned bcr(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; return bcr(n-1,k)+bcr(n-1,k-1); } void test() { for (n=10;n<=35;++n) printf("%u %u",n,bcr(n,n/2); //  C++   cout<<n<<" "<<bcr(n,n/2)<<endl; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

unsigned intになったすべてが正しく計算されました。 ここでは、n = 34の​​行が約1分と見なされています。 C（n、n / 2）を計算すると、2つの再帰呼び出しが行われるため、計算時間は指数関数的にnに依存します。 対処方法は、不正確または遅いです。 解決策は、64ビット変数を使用することです。



ディスカッションの結果に関するコメント：記事の最後に、ディスカッションの参加者の1人に「暗記付きのbcr」の簡単で迅速なバージョンを提供するセクションが追加されます。

64ビットタイプを使用してC（n、k）を計算する

bciのunsigned int関数をunsigned long longに置き換え、n = 34..68の範囲でテストします。 n = 34はbciが正しく考慮される最大値であり、C（68.34）〜2.8 * 10 ¹⁹はもはや符号なしlong long〜1.84 * 10 ^19に適合しません

 unsigned long long bcl(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; unsigned long long r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return r; } void test() { for (n=34;n<=68;++n) printf("%llu %llu",n,bcl(n,n/2)); //  C++   cout<<n<<" "<<bcl(n,n/2)<<endl; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

エラーは、bciと同じ理由でn = 63で発生することがわかります。 最初に63で乗算し（オーバーフロー）、次に31で除算します。

n> 67の精度と計算のさらなる向上

エラーはn = 63で発生し、n = 68で結果はunsigned64に適合しなくなりました。 したがって、「n <= 62まで、bcl関数は正しく考慮します。精度をさらに高めるには、int128または長い演算が必要です」と言うことができます。 非常に高い精度は必要ないが、n = 100 ... 1000での二項係数を検討したい場合 繰り返しますが、bciプロシージャを使用して、unsigned int型をdoubleに変更します。

 double bcd(int n,int k) { if (k>n/2) k=nk; //    k, nk..    C(n,k)=C(n,nk) if (k==1) return n; if (k==0) return 1; double r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } return ceil(r-0.2); //    ,    //    :   ,      //    . -   0.5   round   } void testd() { for (n=50;n<=1000;n+=50) printf("%d %.16e\n",n,bcd(n,n/2)); //  C++   cout<<n<<" "<<bcd(n,n/2)<<endl; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

n = 1000でも、数えることができました！ n = 1030で二重オーバーフローが発生します。

bcdの計算と正確な値の不一致は、n = 57で始まります。 小さい-わずか8。n= 67では、偏差は896です。

極値と「オリンピック選手」向け

原則として、実際の問題については、bcd関数の精度は十分ですが、オリンピアッド問題では、テストはしばしば「エッジで」行われます。 つまり 理論的には、doubleの精度が十分でなく、C（n、k）が符号なしlong longにかろうじて突入するという問題があるかもしれません。 このような極端な場合にオーバーフローを回避する方法は？ 再帰アルゴリズムを使用できます。 ただし、n = 34の​​場合は1分、n = 67の場合は100年がカウントされます。計算値を覚えておくことができます（発行後の付録を参照）。また、すべてのnとkではなく「十分に大きい」だけに再帰を使用できます。 以下は、n <= 67で正しくカウントされる計算手順です。 小さいkのn> 67の場合があります（たとえば、C（82.21）= 1.83 * 10 ¹⁹と見なされます）。

 unsigned long long bcl(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; unsigned long long r; if (n+k>=90) { //    ,   r=bcl(n-1,k); r+=+bcl(n-1,k-1); } else { r=1; for (int i=1; i<=k;++i) { r*=n-k+i; r/=i; } } return r; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

いくつかのオリンピアードの問題では、n> 70の場合、大量のC（n、k）を計算する必要がありました。 それらは明らかに符号なしlong longには適合しませんでした。 当然、私は「長い算術演算」（自分のもの）を使わなければなりませんでした。 このタスクのために、「メモリを使用した再帰」を作成しました。計算された係数は配列に格納され、計算時間の指数関数的な増加はありませんでした。

公開後の追加

議論するとき、計算された値を保存するオプションがしばしば言及されます。 動的メモリ割り当てを備えたコードを持っていますが、引用しませんでした。 現時点では、 chersanyaのコメントから最も簡単で効果的なものがここにあります ： http : //habrahabr.ru/post/274689/#comment_8730359http : //habrahabr.ru/post/274689/#comment_8730359

 unsigned bcr_cache[N_MAX][K_MAX] = {0}; unsigned bcr(int n,int k) { if (k>n/2) k=nk; if (k==1) return n; if (k==0) return 1; if (bcr_cache[n][k] == 0) bcr_cache[n][k] = bcr(n-1,k)+bcr(n-1,k-1); return bcr_cache[n][k]; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

プログラムが（ほぼ）パスカルの三角形のすべての係数を（特定のレベルまで）使用する必要がある場合、記憶を伴う再帰アルゴリズムが最速の方法です。 同様のコードは、符号なしlong longおよびlong算術にも適しています（ただし、必要なメモリ量を動的に計算して割り当てる方がおそらくよいでしょう）。 特定のN_MAX値は次のとおりです。

35-すべての係数C（n、k）をカウントします。符号なし整数（32ビット）の場合はn <35

68-すべての係数C（n、k）をカウントし、符号なしlong long（64ビット）に対してn <68

200-係数C（n、k）、n <200、および符号なしlong long（64ビット）のkをカウントします。 たとえば、C（82.21）=〜1.83 * 10 ^19の場合

K_MAX-これはN_MAX / 2 + 1ですが、C（68.34）は海外で符号なしlong longであるため、35以下である可能性があります。

簡単にするために、K_MAX = 35を常に使用し、「入力-入力しない」とは思わないようにします（ビット容量が64ビットを超える数値に到達するまで）。

Python二項係数の計算

この追加は、記事の公開後の天気について表示されました。 著者はPythonを習得し始め、トレーニングのために、以前にC ++で作成されたolympiadの問題を解決しました。 正確/長い計算に関連するタスクの場合、早期のオーバーフローを回避するためにあらゆる方法で（二項係数の計算のように）計算するか、精度の損失に耐える（二重型になることによる）か、長い計算を書く（または探す）必要があります。 Pythonでは、長い算術演算がすでに存在するため、ここでは記憶を実装して二項係数を計算するだけで十分です。 リストにそれらを記憶します（papameterとして関数に渡されます）。

 #     ,  / #     bcs  ,   n=4  k=2 def Binc(bcs,n,k): if (k>n): return 0 if k>n//2: k=nk #      -   if k==0: return 1 if k==1: return n while len(bcs)<n-3: #   for i in range(len(bcs),n-3): r=[] for j in range(2,i//2+3): r.append(Binc(bcs,i+3,j-1)+Binc(bcs,i+3,j)) bcs.append(r) r=bcs[n-4] if len(r)<k-1: #   for i in range(len(r),k-1): r.append(Binc(bcs,n-1,k-1)+Binc(bcs,n-1,k)) return bcs[n-4][k-2] #   #    C(1000,500) bcs=[] #     t1=time.clock() print(Binc(bcs,1000,500)) t2=time.clock() print(t2-t1) #        for n in range(0,16): print("n=%2d " % n,end="") for k in range(0,n+1): print("%5d" % Binc(bcs,n,k),end="") print()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここに結論があります（プレートなし）

270288240945436569515614693625975275496152008446548287007392875106625428705522193898612483924502370165362606085021546104802209750050679917549894219699518475423665484263751733356162464079737887344364574161119497604571044985756287880514600994219426752366915856603136862602484428109296905863799821216320

0.4200884663301988

この比率では0.5秒未満

C（68.34） （これはlong longに収まらないことを思い出します）0.017秒カウントされ、28453041475240576740に等しくなります