ほとんどのオーディオ形式は、振幅対時間の形式（たとえば.wav）または周波数変換係数（.mp3、.aac、.ogg）の形式で情報を保存しますが、最新のデジタル信号処理アルゴリズムはサウンドの周波数成分で機能します。 振幅領域から周波数領域への二重遷移を処理する必要があります。 現時点では、品質を損なうことなくこのような移行を実装することは、多くのあいまいなソリューションでかなり一般的な問題です。
信号を周波数に分解するために、多くの分野で一般的なフーリエ変換が使用されます。 ほとんどのデジタル信号処理アルゴリズムは、特定の時点の信号振幅データのサンプルを処理する必要があるため、フーリエ変換の多くの変更の1つである離散フーリエ変換を使用すると便利です。 古典的な解釈では、フーリエ変換は次の形式の合計です。
ここで、 Nは分解成分の数、
xn、n = 0 ... N-1-時点番号nでの信号の値、
Xk、k = 0 ... N-1-目的の周波数値を表す出力変換値、
kは周波数インデックスです。
直接変換の結果として得られるXkの値は、Re（Xk）+ i * Im（Xk）のペアの複素数値のセットを表し、高調波信号の振幅と初期位相を特徴づけます。 得られた値に逆フーリエ変換を適用する
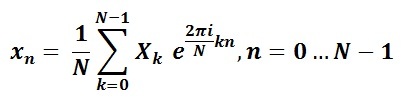
元の信号をある程度の精度で復元します。 実際には、多くの場合、大量のデータを処理する必要があります。 計算を大幅に高速化するために、多くの最新のライブラリでFFT（高速フーリエ変換）と呼ばれる高速フーリエ変換を使用しています。 FFTは複素数でも機能し、変換自体のサイズは必然的に2のべき乗であるという点で異なります。実際には、これはほとんどの場合1024または2048です。逆フーリエ変換、および出力は元の周波数です。つまり、コードのサウンディングシーケンスを取得することは特に難しくありません。
しかし。 あらゆる種類のフーリエ変換は複雑な汎用ツールであり、提供されるデータに大きく依存します。 連続フーリエ変換は、より一般化された、結果として得られる周波数の値が複素数であるフーリエ級数の概念を発展させたものです。 古典的な直接変換を見る
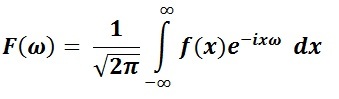
そして、その実装には、離散変換での無限区間での積分があります。これは、シリーズの無限の合計です。 そして、初期関数が無限の長さの関数であり、無限の信号が提示された場合にのみ、右部分と左部分の等価性の妥当性について話すことができます。 実際には、そのような信号はほとんど見られないということには同意しやすい。
2つの異なるオクターブ（周波数はそれぞれ440 Hzと3440 Hzに等しい）で取得されたAノートに対応する人工信号を作成し、直接フーリエ変換を通過させてから、反対を通過させます。
dt = 0.001; T = 1; t=0:dt:T; w = 440; q = 2^(1/12); // x = cos(2*%pi*w*t*q^1) + cos(2*%pi*w*t*q^4); scf(0); plot2d(x, rect=[0,0,1200,2]); // y = fft(x); scf(1); plot(y); // z = fft(y,-1); z1 = z/(T/dt); scf(2); plot2d(x, style=[color("red")], rect=[0,0,1200,2]); plot2d(z1,style=[color("green")], rect=[0,0,1200,2]);
Scilabコードを実行すると、元の信号（ x ）と逆変換（ z1 ）によって取得された信号は、多少の差があります。
図1元の信号の関数x（赤）と復元された信号z1（黄色）のグラフ
そのような制限を無限に回避する方法は？ 信号はブロックでのみFFTを使用して周波数表現に変換されるため、そのようなブロックごとにサンプリング周波数を上げ、FFTブロックのサイズを増やし、それに応じて変換係数の数を増やすことができます。 これにより、単位時間あたりのより正確な周波数結果が得られます。 かなり合理的なアプローチ。
しかし、ギャップの長さをどのように無限大に近づけても、不正確さが発生します。 FFTは、関数のソース高調波については何も知りません。 私たちのケースでは、440 Hzの周波数があり、FFTは元の値に近いものの、歪んだ周波数を持つ高調波のセットに変換しました。 したがって、取得された信号値は元の値に近いだけです。 この歪みを解消するために、いわゆるウィンドウ関数が使用されます。 分解の前に、FFTブロックに窓関数W（ω-t）が乗算されます。ここで、 tは現在のカウントに対応する時刻です。 窓関数の主な影響は、分解における虚数周波数の前の係数を減らすことであり、それによって最終的な周波数画像への寄与を減らします。
しかし、真に「重要でない」周波数ピークをカットしたことをどのように理解できますか？ もちろん、パーティションとその長さ、窓関数の外側の係数がゼロのギャップの長さを試してみることができますが、これは最終的な画像を部分的に滑らかにするだけです。 たとえば、目的のノートの周波数が十分に低い場合を考えてみましょう。ここでは、ソース素材を大幅に超える想像上の周波数を取得できます。
さまざまな種類のウィンドウ関数を使用して実験することは、すでに明らかに価値があります。 たとえば、古典的な長方形のウィンドウ関数
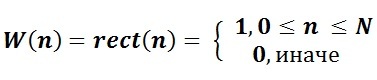
すべての元の周波数を保存します。 しかし、たとえば、三角形の窓を取る場合
エッジのノックアウト値が単純に切り取られることが明らかになり、最も純粋な情報が残る可能性が非常に高くなります。
しかし。 繰り返しますが、単純な制限された信号を生成し、そのスペクトルを計算します。
scf(0); t=0:0.0001:3*%pi; x = sin(t); plot2d(t,x); y = simp(fft(x)); scf(1); plot2d(y, rect = [-100, -10000, 40000, 10000]); disp(y(1000));
元の信号x：
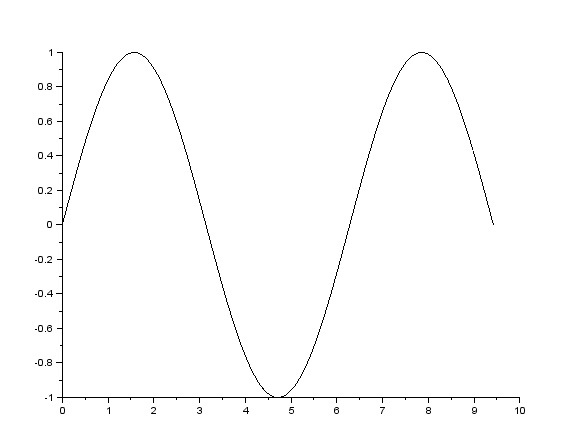
図2元の信号x
図3信号yのスペクトル
何が見えますか？ スペクトルは制限されなくなり、両側で過剰な値が形成され、さらにそれらの無限の数が形成されました！ どうしたの？ ウィンドウ関数のエッジと接触したこれらの2つのポイントでは、関数は滑らかでなくなりました。 入力では、フーリエ変換は単純な正弦波の合計を表す信号を期待します。ここで、ブレークポイントはこれらの正弦波の無限の合計を使用してのみ取得できます。
現在、信号処理分野で最も現実的な不確実性の原則に直面しています。 ここでの原理は、ベネディクの定理と呼ばれます。時間範囲と周波数範囲で関数を同時に制限することはできません。 より厳密な定式化では、定理は次のようになります。空間における関数
およびそのフーリエマッピング 
制限されたルベーグ測度のカバーで同じ機能キャリアを同時に持つことはできません。 そして、無限の長さの信号をほとんど処理する必要がなく、この領域が練習にとってそれほど重要ではない場合、信号の長さが有限である場合はどうでしょうか？
そして、ここでは、音響信号処理の理論で最も有名な定理-コテルニコフ-ナイキスト-シャノンの定理、なしではできません。その解釈の1つでは、次のように聞こえます：アナログ信号は、値がサンプルのf> 2Fmax、ここでFmaxは元の信号のスペクトルが制限される最大周波数です。 この定理とベネディクの定理に基づいて、現時点では、離散的で制限された形式で無限に高い精度で表現できる実際の信号は存在しないと結論付けています。 常に無限に長い信号を処理するか、限られた信号でさまざまな程度の不正確さを受け取ることになり、最終的に元のオーディオ録音の画像を著しく損なう可能性があります。
もちろん、サウンドを扱うこのようなサービスの開発者は、ある程度この問題を解決します。 ステップワイズ補間、さまざまなタイプの線形補間、ローパスフィルターを使用して、サンプリング周波数の半分を超えるサンプルに対処します。 最も一般的な欠点は、元の周波数値に大まかにしか近似されていないデータと、高周波デブリの存在です。 ただし、対処しなければならないオーディオ録音も理想からはほど遠いものです。 高ノイズ、録音速度、音質。 ここでは、各信号に適応し、ゲームの速度、和音の長さを計算し、ホワイトノイズを減衰させる必要がありますが、これはまったく別の話です。