こんにちは、Habr！



この投稿は、約3週間前のLudum Dare 34コンテストへの私の参加に関するものです。



その結果、Growing Sakuraというパズルができました。そのゲームプレイはGIFで見ることができます（心配しないでください。重量は300Kbだけです）。









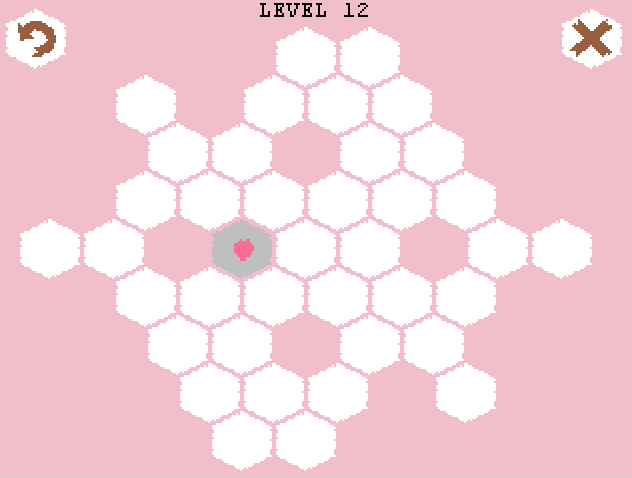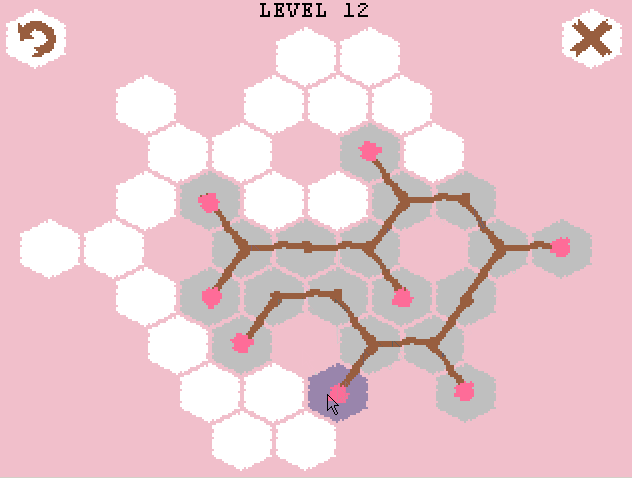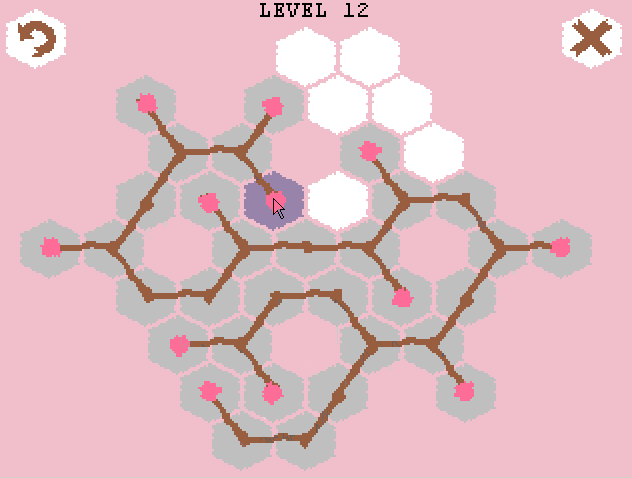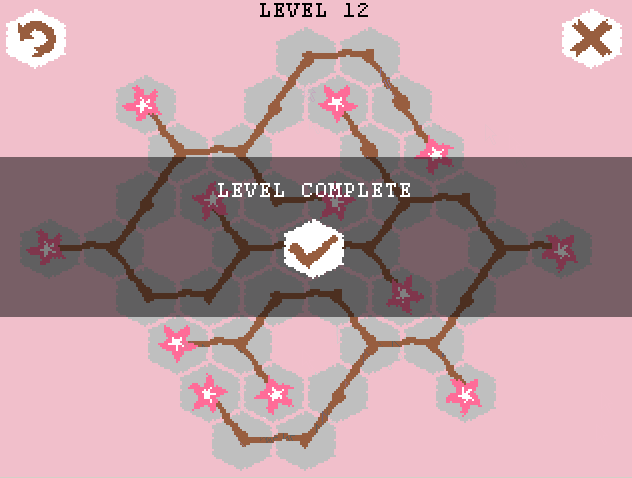
ゲームのルールについて簡単に説明すると、最初は六角形のフィールドといくつかの根芽（または上記のGIFのように1つ）があります。 そこから3つのブランチを開始できます（2つの方法-マウスの左または右ボタンをクリックして）。 ブランチの左の各芽を使用して、マウスの左クリックでYブランチを作成し、さらにブランチをさらに右に続けることができます（Iブランチ）。 ブランチがどの方向にも成長できない場合（対応するセルがビジーであるか、正しい方向にセルがない場合）、ブランチは成長しません。 最後の条件に従って、ブランチの「展開」の順序を正しく選択する必要があります。 結果は、2つの隣接する枝の間に鋭い角がないようなツリー（または複数のツリー）です。 ゲームの目的は、競技場のすべてのセルをカバーすることです。



カットの下を見ないで、10秒間考えて、このゲームがどれほど難しいかを考えてみてください。

Ludum Dareとは何ですか？

このコンテストは4か月に1回開催され、今回はすでに34回目のイベントでした。 競争の本質（コンポ指名）：特定のトピックに関するコンピューターゲームを作成するのに48時間かかります。 このトピックは、コンテストの最初の数分で知られるようになります。 ゲームは単独でゼロから作成する必要があります（すべてゼロから：コード、グラフィック、サウンドなど）。ただし、サードパーティのプログラムとコード開発を使用することは許可されていますが、事前に発表する必要があります（たとえば、Ludum Dare Webサイトのブログに書き込みます） Paint、Unity、C ++、Delphiを使用します。スタータープロジェクトテンプレートへのリンクはこちらです）。 また、単純化されたリラックスジャムノミネートもあります。72時間ものゲームをチームにしたり、古い実績を使用したり、ゲームの最後にソースコードを公開したりする必要はありません。 しかし、私は個人的にジャムのノミネートには興味がありません。48時間を満たす時間がない場合にのみ参加することもあります。



コンテストのテーマは投票によって決まります。今回は、「成長中」と「2つのボタンコントロール」という2つのトピックが一度に最大の投票数を獲得しました。 これらのトピックのいずれか、または両方を一度に使用できます。 トピックの解釈は参加者の裁量に留まります。たとえば、最初のトピックは「成長」、「成長」または「成長」と解釈され、2番目は「2つのボタンの管理」または「2つのボタンの力」と解釈されます。 上記のゲームの説明からわかるように、ある意味で両方のテーマを組み合わせました。

初日

私が目を覚ましたとき、競争はすでに数時間続いていました。 明らかな解決策のトピックは提供しませんでした。 ゆっくりと朝食をとり、コーヒーを注いで、私はこのトピックに興味をそそるほど面白いものを考えていました。 もちろん、私は両方のトピックを一緒にしたかったです。 いくつかの概念が浮上しました：

• ウィンドウマネージャーがエミュレートするパズル：画面には多数のウィンドウがあり（それぞれ2つのボタンがあります！）、閉じる必要がありますが、使用可能な両方のボタンが非常に難しい操作を実行することがあるため、すべてが複雑です（たとえば、このボタンの右側のウィンドウを閉じます）。 ジョークとして、「同意」という見出しのウィンドウを作成し、「同意する」と「同意しない」の2つのボタンを備えた「Bla-bla-bla-bla」のようなテキストでウィンドウを閉じることでした。
• ベーグル戦略：地下基地の開発。 ベースは正方形のタイルで構成され、各タイルで2つのアクションのいずれかを実行できるため、ベースが拡張（成長）します。
• ユニットの束で構成される奇妙なメカニズムには、各ユニットに「オン」と「オフ」の2つのボタンがあります。
• 繰り返しますが、今回は入植者IIの最小限のクローンです。 タイルは六角形で、2つのアクション（道路の追加または家の建設）のいずれかを行うことができます。 急勾配の建物を建設するには、タイルに複数の道路を設置する必要があるという考えでした。 しかし、一枚の紙での実験は、道路がどういうわけかすぐに終わり、集落の成長を止めることを示しました。

これらの概念はすべて退屈であるか、実装するには複雑すぎます（そして、この競争の前に1か月の仕事と勉強のラッシュがあったので、それを緊張させたくありませんでした）。 スーパーヘキサゴンクローンを作成するというアイデアもありました（2つのボタンコントロールがあります！）が、「成長」がなかったため、このアイデアを採点しました。 日中には、入植者の概念を簡素化することで得られた次の概念が現れました。

• いくつかのセル-石、いくつかの豆-に六角形のフィールドがあります。 そして、豆からいくつかの植物の根を育てなければなりません。 根は、この投稿の冒頭で説明したルールに従って成長します。 Beanごとに、Beanツリーが大きく健全に成長するためにルートシステムがカバーする必要があるセルの数がわかっています。 プレーヤーの仕事は、すべての豆が成長するように根を成長させることです。

ゲームのルールは、次の数学的問題から生じました。







そのため、このようなルールに従って、かなり複雑なパズルを作成できると思いました。



ゲームの仕組みのプロトタイプをすぐにスケッチしました。



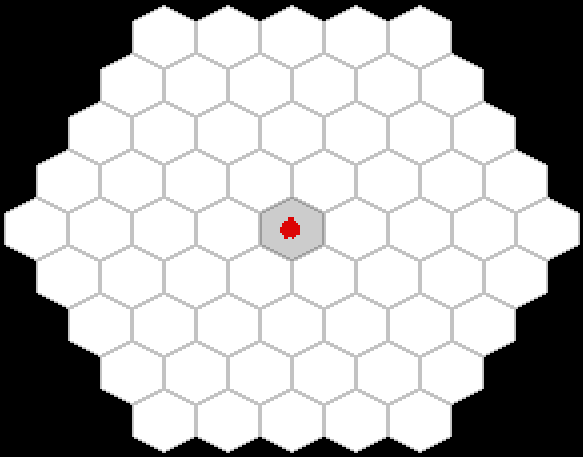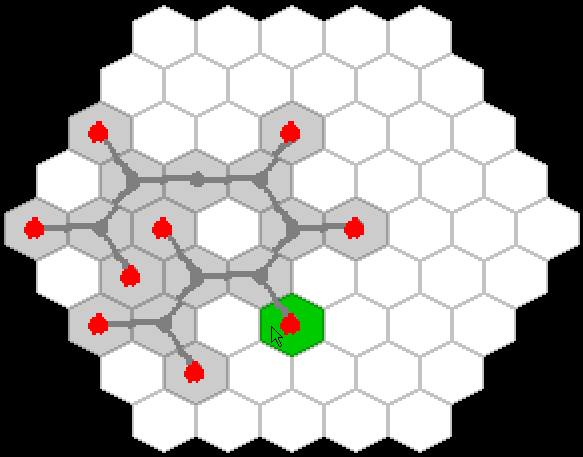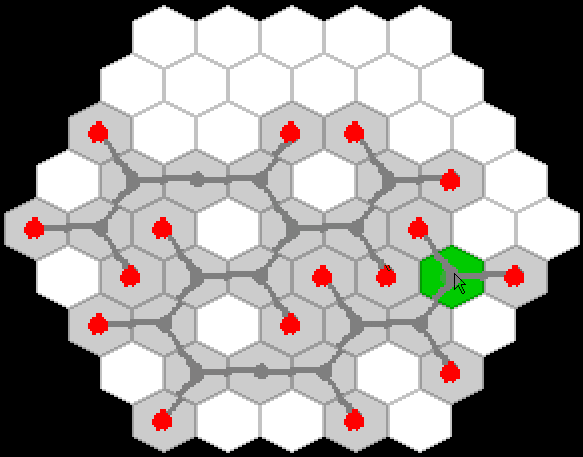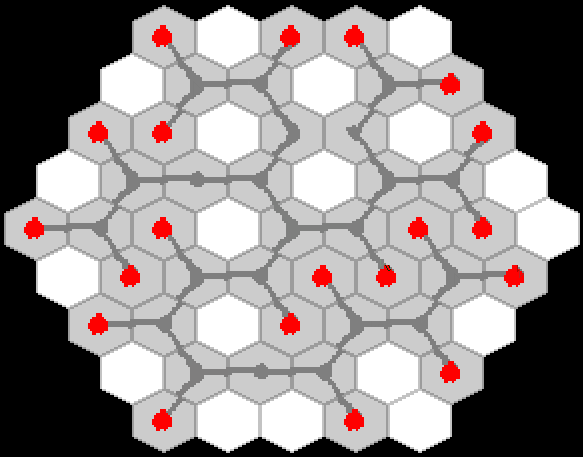
そして、私はそれが良かったのを見ました！



1日目の終わりに、根の成長のアイデアは、桜の枝の成長のアイデアに変換されました（ただし、ゲームコードでは、すべてのオブジェクトはまだ根に従って命名されています！）。 ゲームを簡素化するために、すべての数字が捨てられ、ゴールは最も単純な定式化に縮小されました。競技場全体をカバーするだけです。 ゲームのプロトタイプは次のように成長しました。



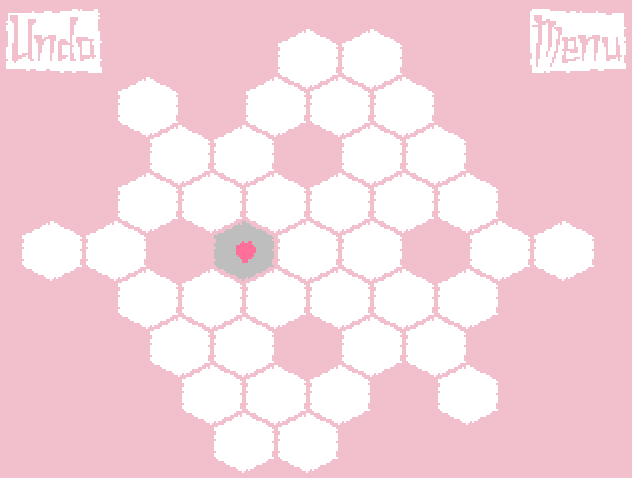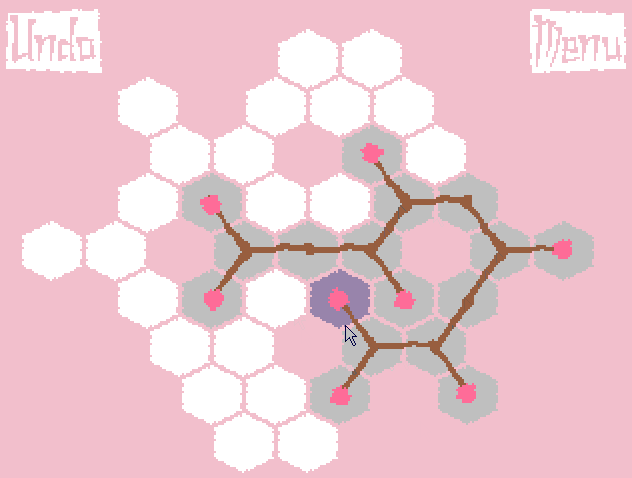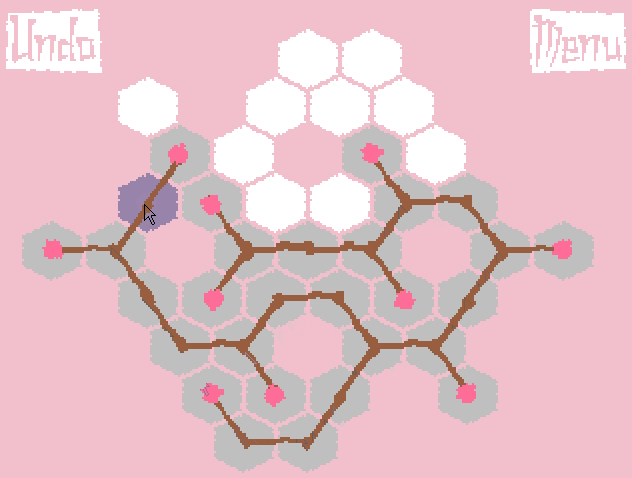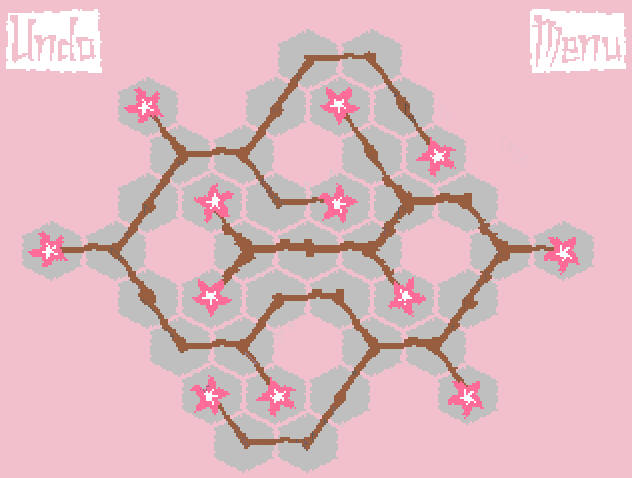
最も遠い葉までの距離に応じて木の枝を太くするというアイデアがありました（これはgifで見ることができます）。 しかし、長い枝の場合、伸びが非常に大きくなり、外観が悪化しました。 私はすべてを美しく仕上げるために多くの時間を費やしました。 その結果、彼は得点しました-さらに多くのことをしなければなりませんでした。 これ以降、すべての枝は同じ厚さのままでした。



これで、私は最初の日を終えることを決めて、寝ました。

二日目

いつものように、最初の日の後の夢で、私は救うことを決めなかったが、代わりに二夜目は眠らない。 午前中、レベルを考えて座っていました。 彼はWordで六角形のグリッドをスケッチして印刷し、鉛筆と消しゴムでさらに振り回しました。 自動ソルバーがなければ継続するのは難しいことが明らかになりました。



すぐに言ってやった。 C ++で簡単なパズルソルバーをスケッチしました。 プレーヤーの可能なすべてのアクションを再帰的に反復し、解決されたパズルを確認します。 列挙の各反復で、ゲームの現在の状態はstd :: setに保存されます。 後で同じ状態のゲームがある場合、検索はロールバックされます。 したがって、ソルバーは同じシナリオを100倍考慮することはありません。



上記の2つのGIFのパズル（パズルAと呼びましょう）には、47種類ものソリューションがあります。 10810046のゲーム状態が考慮されている間、完全に検索するのに93秒かかりました。 このソルバーは将来的に大いに役立ちました。



異なるレベルのソルバーの例：







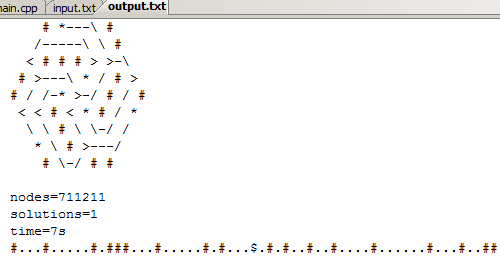
このレベルは7秒で解決され、7111211の状態はstd :: setに保存され、正確に1つのソリューションが見つかりました。 一番下の奇妙な線は、ゲーム自体にすでに挿入されているレベルの説明です。



少し後、ソルバーはヒューリスティックな「孤独なセル」によって最適化されました。 つまり、あるステップで、空きセルの1つが占有セル（「壁」または桜の枝がすでに成長しているセル）に囲まれていることが判明し、隣接するセルからこのセルに枝を入れることが不可能な場合、解決策がないことが明らかになりましたそして、バストはロールバックしました。 このヒューリスティックを追加すると、パズルAは5秒で処理され始め、状態の数は723225になります。



2日目の終わりまで、私は面白いゲームグリッドを手で描き、プログラムでそれらを解決しました。 その間に、ゲームにメニューを追加しました（まあ、ソルバーがソリューションを列挙するときに他に何をしますか？）、アイコンを再描画しました。 ゲームは次のようになり始めました。







gifからわかるように、40ものパズルを開発するという、かなり野心的なタスクを設定しました。 gifの作成時までには、40のうち17レベルしか準備ができていませんでしたが、コンテストが終わるまで、まだ10時間ほどの夜がありました。



いくつかのレベルは次のように生成されました。ある種の対称的な図が描かれ、根芽がそのランダムなセルに突っ込まれました。 その後、ソルバーが起動しました。 得られたソリューションが多すぎるかまったくないことが判明した場合-レベルをわずかに変更し（形状を少し変更するか、ルートスプラウトを別の場所に移植します）、ソルバーが再び起動し、適切なレベルが構築されるまで続きます。



他のレベルでは、図は意図的に非対称であり、通常、桜のいくつかの枝が共通の「塊」に収束します。その後、それらを慎重に編む必要がありました。 これらのレベルもソルバーを使用して作成されました。



次に、いくつかの根芽を持つレベルを追加し始めました。 ゲームはすぐにさらに多様になりました！ いくつかの芽があるレベルの例：



はい、1つのセルだけをカバーしてレベルを達成できない場合があります...



夜になると、ゲームのルールを含む画面をゲームに追加し、素晴らしいBosca Ceoilプログラムを使用していくつかのサウンドを作成し、最終的に40のレベル（40、Karl！）をすべて仕上げました。 最後のレベルは非常に複雑であるため、私のソルバーには完全には受け入れられません。彼は目の前でいくつかの解決策を見つけ、記憶がどのように終わり、クラッシュします。 したがって、ゲーム内のすべてのパズルには解決策があると自信を持って言えますが、ソリューションの数は正確にはわかりません。



ゲームは最後の1時間で終了し、すでにコンテストウェブサイトに残っていた手を弱めていました。











コンテストの後、主催者は投票に3週間を与えます。 Ludum Dareメンバーは、他のメンバーのゲームをダウンロードして評価します。 私もこれを約1週間行いましたが、同時に、Growing Sakuraゲームがどれほど難しいかを考えていました。 その結果、すべてが次のようになりました。

成長している桜はNP困難です

ここで、証拠を述べようとします（どこかでそれを台無しにしないでください！）。



この記事では、平面立方3連結グラフのハミルトニアンサイクルの存在をチェックする問題がNP完全であることの証拠を見つけることができます（簡潔にするためにXと呼びましょう）。 すぐに理解できない単語をすべて解読します。



グラフはいくつかのポイント（頂点と呼ばれます）であり、そのいくつかのペアは線で結ばれています（エッジと呼ばれます）。 グラフは、エッジが交差しないように平面に配置できる場合、 平面と呼ばれます。 グラフは、頂点のそれぞれから正確に3つのエッジが出ている場合、 キュービックと呼ばれます。 グラフの少なくとも2つの部分のために少なくとも3つのエッジを削除する必要がある場合、グラフは3接続と呼ばれます。 グラフのハミルトニアンサイクルは、ペアごとに異なる頂点v ₁ 、v ₂ 、...、v _nのシーケンスであり、v _iとv _{i + 1}は1 <= i <nのエッジで接続され、頂点v _nとvはエッジで接続されます₁ 、ここでnはグラフ内の頂点の数です。 たとえば、次の図は、平面立方3連結グラフのハミルトニアンサイクルを示しています。











NP難易度とNP完全性の定義はそれほど単純ではありません。 しかし、私はネタバレの下で問題を簡単に説明しようとします。







形式的には、問題XとゲームGrowing Sakuraを解決可能性の問題として定式化します。



問題X：「立方平面3連結グラフGを考えると、その中にハミルトニアンサイクルが存在するのは本当ですか？」



Game Growing Sakura：「Growing Sakuraのレベルを考えれば、彼に解決策があるのは本当ですか？」



さて、NP完全問題XをゲームGrowing Sakuraに還元します。つまりタスクXの入力を使用して、Growing Sakuraのレベルを構築し、そのソリューションが元の問題Xの答えを提供するようにします。これにより、タスクXはゲームGrowing Sakuraほど複雑ではないことがわかります。



これを行うには、次の設計が必要です。

ANDガジェット

ここではすべてがシンプルです。3つの側面のいずれかから来た桜の枝は、同時に両方向にさらに成長できます。

ORガジェット

この要素の場合、sakuraブランチは2つのうち正確に1つの方向を選択する必要があります（実際、1つだけですが、このアクションは無意味です）。2番目の方向については、後で説明する必要があります。

片道ガジェット

この設計は一種のダイオードです。彼女は一方向の桜の枝を逃します。





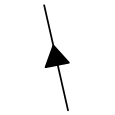
つまりこの方向にスキップします：





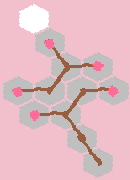
しかし、この方向ではそうではありません：





追加のルートポイントなしでは同じデザインを思い付くことができませんでした、できますか？

ロックガジェット

最も複雑な要素であるその構築には、かなりの時間がかかりました。





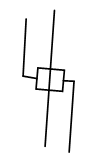
この要素の本質は次のとおりです。次の構成でのみ解決策があります。a

）





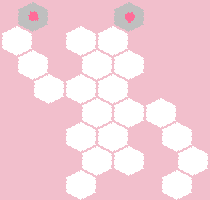
b）





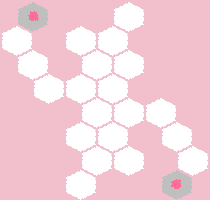
この場合、次の構成には解決策がありません。





さらに、「孤独なセル」状況を受信せずにクロスをカバーすることさえできません。

さあ、すべてをつなぎましょう！

ORガジェットから、平面立方3連結グラフの最初の近似を収集することはすでに可能です。しかし、ゲームのルールでは、特にハミルトニアンサイクルに含まれないエッジをカバーする必要があります。これを確実に行うには、よりかさばる設計が必要です。これは



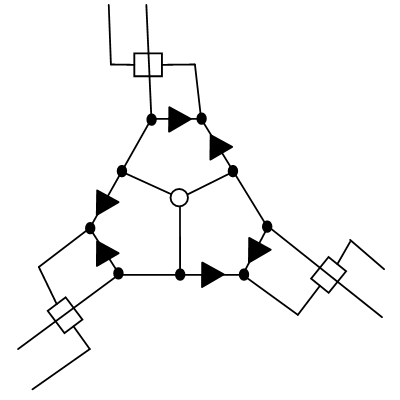
次のとおりです。この構造は、3次グラフの1つの頂点に対応します。



それでは、その仕組みを見てみましょう。一般性を失うことなく、桜の枝が左下から来るようにします（一度に2つのパスに沿って）。次に、スキームの次の部分について説明します：





ここで、選択した2つのオプションのどちらに応じて、次の開発が行われます：



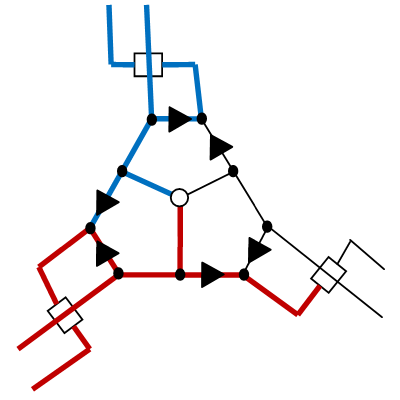
どちらの場合も、2つの桜の枝を1つの方向に送信し、そのうちの1つを別の方向に送信します。つまり一方の方向ではグラフのエッジをペイントし、もう一方の方向では-いいえ。今、私たちの我々はエッジを塗装されていない、グラフ、のピークのパスハミルトン経路に到達し、LOCK-ガジェットのロックを解除し、カバーにあなたが必要なすべてをカバーします（緑色で下に示されている）別のブランチが、そこに来るとき：





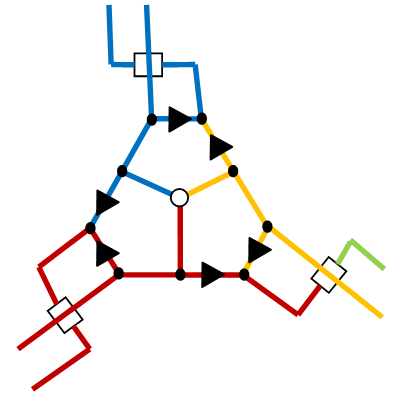
我々のケース私たちの方法ですでに1つまたは2つの近隣のピークにアクセスしているピークに達した場合、読者自身が確認することを提案します。



さて、今では平面立方体3連結グラフ全体について巨大なレベルを構築し、解決策があるかどうかを確認します。存在する場合、元のグラフのサイクルを復元することは難しくありません-桜の枝がORガジェットでどのように成長するかを見てください（正式には、明示的に復元する必要はありません）。このようなレベルはいつでも作成できます。すべてのガジェットは、十分な長さのセルのチェーンで回転および接続できます。グラフは最初は平面であるため、パスの交差の問題を解決する必要はありません。



すべてが証明されたように思えますか？いいえ、証明されていません。構築されたレベルにはまったく解決策がありません-「連鎖反応」のプロセスを開始していません-ハミルトニアンパスには開始する場所がありません。それは非常に簡単に解決されます。任意のエッジ（または、対応するLOCKガジェット）を使用して、これを実行します。



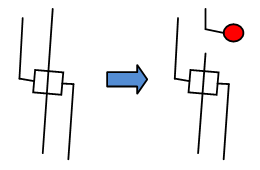
赤い円は、ブランチの成長を開始する場所です。そして、ハミルトニアンサイクルが閉じられるように、必ずブレークエンドをカバーする必要があります！



今、あなたはそれを証明しましたか？いやいや！グラフには突然、ハミルトニアンサイクルがあります。どうする？もう一方の端からループを探してみてください。明らかに、同じ頂点から出現する2つのエッジの少なくとも1つは、目的のハミルトニアンパス（存在する場合）を通過します。したがって、問題Xを解決するには、Growing Sakuraの2レベル以下のゲームが必要です。



「Let me！」と言います。「Growing Sakuraの1レベルのみを解決することをもう少し上に書いたのです。これは問題Xのグラフに相当します！」そうです、私はあなたをbraしました！ただし、この証拠は悪化しません。私はクックに関する情報のみを使用し、カープに関する情報は使用しませんでした。



現在、Growing SakuraのNP難易度が証明されています！ほら、仲間！

成長するさくらはNP完全です

既知のように、NP困難でクラスNPにある場合、問題はNP完全です。最初の点をもう少し高く証明しました。



この問題のNPへの帰属は明らかです。この問題の解決策が「はい」または「いいえ」のいずれかの答えである場合、タスクはNPクラスに属し、答え「はい」には、答えが多項式時間で本当に「はい」であることを確認できる証明書があります。実際、Growing Sakuraのゲームでは、証明書を長さO（n）の文字列として記述し、対応するセルをクリックした順序とボタンを保存できます（nはフィールド上のセルの数です）。さて、O（n）の場合、証明書が「有効」であることを確認できます-証明書とゲームのルールに従ってブランチを展開するだけです。



やあ、Growing SakuraはNP完全だ！突然、多項式時間で動作するこのゲームのソルバーを誰かが書いた場合、100万を拾うことができます。

おわりに

Growing SakuraがNP完全であるという事実は、このゲームのすべてのレベルが非常に難しいことを意味しません。そのようなレベルを作成できることを意味するだけです。そして、残りはすでにレベル設計に依存しています。多くの古典的な任天堂のゲームはNPハードであることが知られていますが、これはそれらを楽しむことを妨げるものではありません。キャンディークラッシュのようなカジュアルでさえNPハードであり、テトリス、サッパー、その他の数独は言うまでもありません。



Ludum Dareでの投票は明日終了します。更新では、取得した場所を公開します。トップ100ゲームに参加したいと考えています。



リンク：Ludum Dareのゲームページ、Dropbox、Itch.io 。



UPD。さて、これで結果が判明しました。合計で、1232の作品がコンポにノミネートされました。成長するさくらは名誉ある10位になりました（トップ受賞者）。その他の具体的な側面：＃4テーマ、＃5イノベーション、＃22 Fun。