Mathcad Expressは、有名なPTC Mathcad Primeパッケージの「ライト」バージョンであり、ほとんどの機能がオフになっています。 それにもかかわらず、擬似乱数センサーは引き続き利用可能であり、これにより、モンテカルロアルゴリズムに基づいたさまざまな統計モデルを(非常に迅速かつ明確に)実装できます。 Mathcad Primeの商用バージョンのユーザーの観点からは、いくつかのソリューションが最良ではないことをすぐに言わなければなりませんが、無料のMathcad Expressの機能を超えて私たちを導くことはありません。
モンテカルロアルゴリズムは、特定の効果(たとえば、 機器の故障のシーケンス)をシミュレートする特定の擬似乱数のシーケンスのプログラムによる作成に基づく数値的手法のグループの一般名です。 ランダムなプロセスの多数の認識を受け取ったので、その確率的特性が、解決される「現実世界」の問題の同様の値と一致することを期待できます。 MathcadおよびXPS形式でさらに計算されたファイルがここにあります 。
パート1.疑似乱数の選択を生成する方法
Mathcad Expressには、さまざまな分布則で擬似乱数データサンプルを作成する、多数の擬似乱数ジェネレーターが用意されています。 N個の擬似乱数からベクトルを作成するには、Mathcadドキュメントの1行のみが必要です。 たとえば、正規分布(ゼロ平均と単位分散)でN = 5の擬似乱数を生成するには、次のようにします。

グラフ上の乱数ベクトルを次のように視覚化すると便利です:横軸に沿って1つのサンプル(つまり、ランダムベクトルT1の 1つのコンポーネント)、縦軸に沿って別のサンプル(別のランダムベクトルT2 )。 次の図は、指数分布(左)と正規分布(右)の擬似乱数ペアのプロットを示しています。 分布パラメーターは、グラフの上にある式で設定されます。
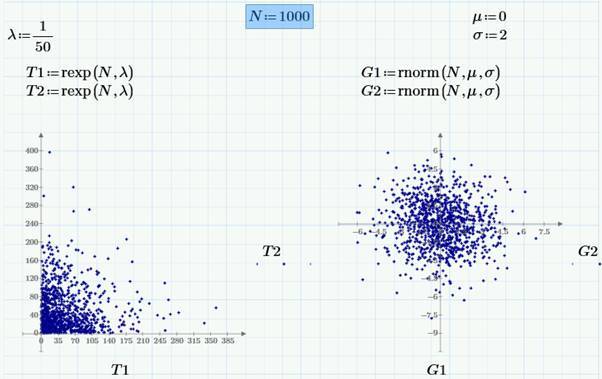
次の図は、正規分布と異なる分散をもつ擬似乱数G1とG3の同様のペア(左側のグラフ)と、相関擬似乱数G1とG4の生成方法(右側のグラフ)を示しています。

一般的に、Mathcad Expressにはかなりの数の擬似乱数センサーが用意されています。
- rnd(x)は、区間(0、x)の均一分布です。
- rbeta(x、s1、s2)-ベータ分布(s1、s2> 0-パラメーター、0 <x <1)。
- rbinom(k、n、p)は二項分布です(nはパラメーター全体、0 <k <nおよび0 <p <1は単一のテストの成功確率に等しいパラメーターです)。
- rcauchy(x、l、s)はコーシー分布です(lは展開パラメーター、s> 0はスケールパラメーターです)。
- rexp(x、r)は指数分布です(r> 0は指数です)。
- rF(x、d1、d2)はフィッシャー分布です(d1、d2> 0は自由度です)。
- rgamma(x、s)はガンマ分布です(s> 0は形状パラメーターです)。
- rgeom(k、p)は、幾何分布です(0 <p <1は、単一のテストの成功確率に等しいパラメーターです)。
- rhypergeom(k、a、b、n)-超幾何分布(a、b、n-整数パラメーター)。
- rlnorm(x、m、s)は対数正規分布です(mは数学的期待値の自然対数、s> 0は標準偏差の自然対数です)。
- rlogis(x、l、s)はロジスティック分布です(lは数学的期待値、s> 0はスケールパラメーターです)。
- rnbinom(k、n、p)-負の二項分布(n> 0-整数パラメーター、0 <p <1)。
- rnorm(x、m、s)は正規分布です(mは平均値、s> 0は標準偏差です)。
- rpois(k、p)はポアソン分布です(p> 0はパラメーターです)。
- rt(x、d)は生徒の分布です(d> 0は自由度の数です)。
- runif(x、a、b)-均一な分布(a <b-間隔の境界)。
- rweibull(x、s)はワイブル分布です(s> 0はパラメーターです)。
パート2.統計計算の実行方法
最も単純な統計式を使用して、平均値、分散、標準偏差のサンプル推定値を計算できます。
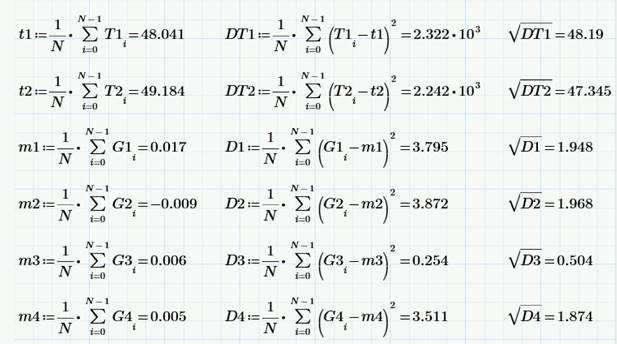
同様に、サンプル相関係数を推定できます。

相関と回帰に関する記事で説明した相関擬似乱数を使用して、サイト訪問者のコンバージョンをモデル化する例。
パート3.ヒストグラムの作成方法
ヒストグラムチャートを作成するための簡単なレシピを次に示します。 Mathcad Primeの商用バージョンでは、1つの組み込み関数を使用することで、ヒストグラムのデータの準備が削減されます。
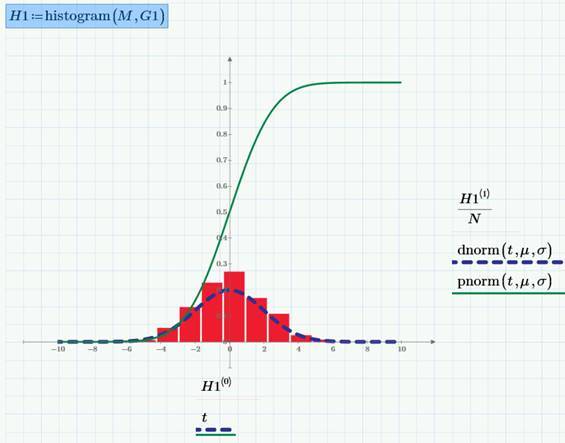
(ちなみに、ガウス擬似乱数サンプルの例で示されているように、確率密度と分布関数の両方について、リストされた分布タイプに組み込み関数も提供されています)。 Mathcad Expressでヒストグラムをプロットするには、データがM間隔に分類される間隔(a、b)を手動で分割し、Mathcad Expressで利用可能な簡単な数学演算を実行する必要があります(読者が興味を持っている場合、ドキュメントで見つけることができます)計算付き )。

例として、指数分布の擬似ランダムデータを使用します(実用的なアプリケーションの1つは、 前の記事で説明されています )。
結論として、ヒストグラムについては、適切なタイプのグラフを選択する必要があることに注意してください。
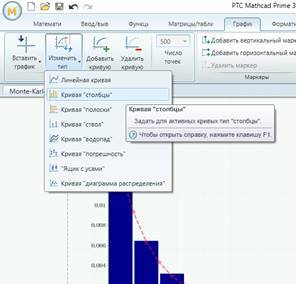
要約すると、無料の数学パッケージRTS Mathcad Expressを使用すると、通常の数学表記で、プログラミングに頼らずにモンテカルロモデルを簡単に実装できます。 また、次の記事で、データ分析におけるMathcadの他のアプリケーションについて説明できることを願っています。