「怖い」Haskellの抽象化。数学もコードもありません（ほぼ）。 パートI

-モナドとは何ですか？

-副作用から純粋な計算を分離するため。

（Haskell言語に関するオンラインディスカッションから）

シャーロックホームズとワトソン博士は気球で飛んでいます。 濃霧になり、方向を失います。 小さなギャップがあります-そして、彼らは地球上の人間を見ます。

-親愛なる、私たちがどこにいるか教えてもらえますか？

「風船かごに入れて」

その後、彼らはそれらをさらに運び、再び彼らは何も見えません。

「それは数学者でした」とホームズは言います。

「でもなぜ？」

-彼の答えは絶対に正確ですが、絶対に役に立ちません。

（冗談）

古代エジプト人が5匹の魚を数えたと書きたいと思ったとき、彼らは5匹の魚の絵を描いた。 彼らが70人を数えたと書きたいと思ったとき、彼らは70人の人物を描きました。 彼らが群れで300匹の羊を数えたと書いたとき、彼らは...-まあ、一般的に、あなたは理解しています。 そのため、古代エジプト人は、最も知的で怠zyな人々がこれらすべての記録に共通する何かを見るまで苦しみ、数えている量の概念を数えているものの性質から分離しました。 そして、別の賢い怠zyなエジプト人は、人々が数字を指定するために使用していた多くのスティックをはるかに少ない文字数で置き換え、短い組み合わせで膨大な数のスティックを置き換えることができました。



これらの賢い怠zyなエジプト人がしたことは、抽象化と呼ばれます。 彼らは、何かの量に関するすべての記録に特徴的な共通点に気づき、この共通点をカウントされたオブジェクトの特定のプロパティから分離しました。 今日の数字と呼ばれるこの抽象化の意味と、それが人々の生活をどれほど楽にしているのかを理解していれば、Haskell言語の抽象化を理解することは難しくありません。 カテゴリの数学的理論から私たちに来た恐ろしい名前にもかかわらず、それらを理解することは「数字」と呼ばれる抽象化より難しくありません。 それらを理解するために、カテゴリーの理論、または高校のボリュームの数学さえも知る必要はありません（算数で十分です）。 また、恐ろしい多くの数学的概念に頼らずに、それらを説明することもできます。 そして、Haskellの抽象化の意味は数字の意味とまったく同じです-プログラマーにとって生活が楽になります（そしてどれだけ想像することもできません！）。



機能プログラムと命令プログラムの違い

純粋な機能の利点を発見する

計算と「その他」

「他の何か」のカプセル化

ファンクターは簡単ではありませんが、非常に簡単です！

適用ファンクターも非常に簡単です！

あなたは笑いますが、モナドも簡単です！

そして、さらにいくつかのモナドを定義しましょう

モナドを適用する

ライターモナドを定義し、モノイドを知る

モノイドとファンクター、適用ファンクターおよびモナドの法則

型クラス：多数の機能が無料で！

I / O：IOモナド



抽象化を理解（および受け入れ）するには、通常、人々はそれらをいくつかの角度から見る必要があります。

最初に、提案された抽象化の形式で複雑さのレベルを追加することで、常に遭遇する非常に高いレベルの複雑さを排除できることを理解する必要があります。 したがって、純粋な関数を使用してプログラマが遭遇することのない膨大な数の問題について説明します（心配することはありません。以下に説明します）。

第二に、提案された抽象化がどのように実装されたか、そしてこの実装がどのように特定のケースではなく非常に多様な異なる状況でそれを使用できるかを理解する必要があります。 したがって、Haskellの抽象化を実装するロジックを説明し、それらが適用可能なだけでなく、信じられないほど多くの状況で大きな利点を提供することを示します。

そして第三に、人々は抽象化がどのように実装されるかだけでなく、それらを日常生活にどのように適用するかを理解する必要があります。 したがって、これについては記事で説明します。 さらに、それは単純ではありませんが、非常に単純です-これらの抽象化がどのように実装されているかを理解するよりも簡単です（そして、説明された抽象化の実装を理解することは難しくないことがわかります）。

ただし、導入は多少遅れたため、おそらく開始します。 記事にはコードがほとんどないので、その抽象化の美しさとパワーを理解して評価するためにHaskellの構文に精通する必要はありません。

機能プログラムと命令プログラムの違い

関数型言語と命令型言語で書かれたプログラムを鳥瞰図で見ると、違いはありません。 これらのプログラムと他のプログラムはどちらも、ソースデータを受け入れ、ソースから変換された他のデータを出力する一種のブラックボックスです。 ブラックボックス内でデータ変換がどのように行われるかを正確に理解するために、ブラックボックス内を確認する場合に違いを確認します。



命令型ブラックボックスを確認すると、それに含まれるデータが変数に割り当てられ、必要なデータを取得するまでこれらの変数が繰り返し変更され、ブラックボックスから発行されることがわかります。



機能的なブラックボックスでは、着信データの発信データへのこの変換は、着信データへの依存の観点から最終結果が表される特定の式を適用することによって行われます。 学校のカリキュラムから、移動の平均速度が何に依存しているか覚えていますか？ そうです：移動したパスと移動した時間から。 初期データ（パスSと時間t ）、および平均速度（ S / t ）の計算式がわかれば、最終結果（平均速度）を計算できます。 最終結果が初期データに依存するという同じ原理に従って、関数スタイルで記述されたプログラムの最終結果が計算されます。 同時に、命令型プログラミングとは異なり、計算のプロセスでは、変数の変更はありません-ローカルでもグローバルでもありません。



実際、前の段落では、単語formulaの代わりに単語functionを使用する方が正しいでしょう。 命令型プログラミング言語の関数という言葉は、数学、物理学、および関数型プログラミング言語でこの用語が意味するものとはまったく呼ばれないことが多いため、私はこれをしませんでした。 命令型言語では、関数はしばしばより正確にプロシージャと呼ばれるもの、つまり、プログラム（サブプログラム）の名前付き部分と呼ばれ、繰り返し発生するコードの繰り返しを回避するために使用されます。 少し後に、関数型プログラミング言語の関数（いわゆるpure関数 、またはpure関数 ）が命令型プログラミング言語の関数とどのように異なるかを理解できます。



注：プログラミング言語の命令型と機能型への分割は、かなりarbitrary意的です。 命令型とみなされる言語では関数型スタイルで、関数型とみなされる言語では命令型スタイルでプログラミングできます（ Haskellの命令型スタイルで階乗を計算し、Cの同じプログラムと比較するプログラムの例です ）-それは単に不便です。 したがって、命令型プログラミングを奨励する命令型言語と、関数型プログラミングを奨励する言語として機能型言語を考えてみましょう。

純粋な機能の利点を発見する

Haskellプログラマーがいわゆる純粋な関数を扱う時間の大部分（もちろん、すべてはプログラマーに依存しますが、ここではどのようにすべきかについて話しています）。 実際、これらの関数は「純粋」と呼ばれるため、命令型プログラミングで「関数」という用語が意味するものと混同されません。 実際、これらは用語の数学的な理解において最も一般的な機能です。 以下に、3つの数字を追加するこのような関数の最も簡単な例を示します。

addThreeNumbers xyz = x + y + z
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

=記号（ 等号 ）に注意してください。 命令型プログラミングとは異なり、割り当て操作を意味するものではありません。 等号は、彼の左にあるものが彼の右にある表現と同じであることを意味します。 数学のように： 6 + 4は10 と同じなので、 6 + 4 = 10と書きます。 どの計算でも、10の代わりに式（6 + 4）を置き換えることができ、10を置き換えた場合と同じ結果が得られます。 Haskellの同じこと： addThreeNumbers xyz



代わりに、式x + y + z



置き換えることができ、同じ結果が得られます。 ところで、コンパイラはまさにそれを行います-関数名に遭遇すると、代わりにその本体で定義された式を置き換えます。



この機能の「純度」とは何ですか？

関数の結果は、引数のみに依存します。 同じ引数でこの関数を何度呼び出しても、関数は外部状態を参照しないため、常に同じ結果を返します。 彼女は外の世界から完全に隔離されており、計算では、私たちが彼女の議論として明示的に伝えたものだけを考慮しています。 歴史などの科学とは異なり、数学的計算の結果は、共産党が権力を握っているか、民主党員か、プーチン大統領かによって左右されません。 私たちの関数は数学に由来します-それは渡された引数にのみ依存し、それ以上には依存しません。



自分で確認できます。この関数の引数として値1、2、4を何回渡しても、常に7になります。「3」の代わりに「（2 + 1）」を渡すこともできます。 「4」-「（2 * 2）」。 これらの引数で別の結果を取得するオプションはありません。

addThreeNumbers



関数は、外部状態に依存しないだけでなく、変更もできないため、純粋とaddThreeNumbers



呼ばれます。 彼女は引数として渡されたローカル変数を変更することさえできません。 彼女ができる（そしてすべき）ことは、彼女に渡された引数の値に基づいて結果を計算することです。 つまり、この機能には副作用はありません。

これにより何が得られますか？ なぜHaskellistsは、ローカルおよびグローバル変数の変異に基づいて構築された命令型プログラミング言語の伝統的な機能を見て、このような軽pur的な方法でその機能の「純度」を保持するのでしょうか。

純粋な関数の計算結果は外部状態にまったく依存せず、外部状態を変更しないため、共通のリソースをめぐって競合するデータの競合を心配することなく、これらの関数を並列に計算できます。 副作用は並列計算の死であり、私たちの純粋な関数にはそれらがないため、心配する必要はありません。 関数を計算する順序や、計算を並列化する方法を気にせずに、純粋な関数を記述するだけです。 Haskellで記述しているからこそ、すぐに並列化できます。

さらに、純粋な関数を同じ引数で複数回呼び出すため、常に同じ結果が得られることが保証されているため、Haskellは一度計算された結果を記憶し、同じ引数で関数が再度呼び出されると、再度評価せずに以前に計算された結果を置き換えます。 これはメモ化と呼ばれます。 これは非常に強力な最適化ツールです。 結果が常に同じであることがわかっているのに、なぜ再びカウントするのでしょうか？

命令型プログラミングの本質が厳密に定義されたシーケンス内の変数の突然変異（変更）にある場合、関数型プログラミングの本質はデータの不変性と関数の構成にあります。



関数g :: a -> b



（「型aの引数を取り、型bの値を返す関数g」と読む）と関数f :: b -> c



がある場合、それらを合成することで関数h :: a -> c



取得できますh :: a -> c



。 タイプaの値を関数gの入力に供給することにより、出力でタイプbの値を取得します-関数fはまさにこのタイプの入力を受け取ります。 したがって、関数gの計算結果を関数fにすぐに転送できます。その結果は、タイプcの値になります。 次のように書かれています。

 h :: a -> c h = f . g
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

関数fとgの間のポイントは、次のタイプの合成演算子です。

 (.) :: (b -> c) -> (a -> b) -> (a -> c)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合成演算子は、通常の関数と同じ方法（括弧内）で括弧内で使用されるため、ここでは括弧で囲まれています。 2つの引数の間で中置スタイルで使用する場合、括弧なしで使用されます。



合成演算子は、関数fに対応する最初の引数として関数b -> c



を取ります（矢印は型-関数の型も示します）。 2番目の引数、彼は関数も受け取ります-ただし、タイプa -> b



、これは関数gに対応します。 そして、構成演算子は、関数h :: a -> c



a -> c



に対応するa- a -> c



型の新しい関数をusに返します。 機能矢印には右結合性があるため、最後の括弧を省略できます。

 (.) :: (b -> c) -> (a -> b) -> a -> c
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、構成演算子は、 b -> c



およびb -> c



a -> b



型の2つの関数と、2番目の関数の入力に転送されるa型の引数を渡す必要があることがわかります。出力では、 c



型の値を取得します。機能。



機能の構成f . g



f . g



はf (gx)



と同じ意味-つまり 関数g



を引数x



適用した結果に適用される関数f









関数の合成が関数型プログラミング言語の本質であるのはなぜですか？ はい、関数型言語で書かれたプログラムは関数の合成に過ぎないためです！ 関数は、プログラムの構成要素です。 それらを構成すると、他の関数を取得し、独自の方法で、新しい関数を取得するように構成します-など。 データはある関数から別の関数に流れ、変換し、関数を構成するための唯一の条件は、ある関数によって返されるデータが次の関数が取るものと同じ型を持つことです。



Haskellの関数はクリーンであり、明示的に渡された引数にのみ依存しているため、関数構成チェーンからある種の「ブリック」を簡単に「引き出し」て、リファクタリングまたは完全に置き換えることさえできます。 注意する必要があるのは、新しいブリック関数が古いブリック関数と同じ型の入力値と出力値で受け入れることだけです。 それだけです！ 純粋な関数は外部状態に依存しないため、関数に関係なく関数をテストできます。 プログラム全体をテストする代わりに、個々の機能をテストします。 私たちの場合、この非常に重要な話で説明されている状況は、単に不可能になります。

マーケティング担当者はプログラマーに次のことを尋ねます。

-大規模プロジェクトをサポートする難しさは何ですか？

「まあ、あなたが作家であり、戦争と平和プロジェクトをサポートしていると想像してください」とプログラマーは答えます。 -あなたはTKを持っています-ナターシャ・ロストワが雨の中で公園を歩いた方法についての章を書きます。 「雨が降っていた」と書いて保存すると、「ナターシャ・ロストヴァが亡くなりました。続行できません」というエラーメッセージが表示されます。 どうして死んだの？どうして死んだの？ あなたは理解し始めます。 ピエール・ベズホフのつるつるした靴、彼が落ち、銃が地面にぶつかり、ポストからの弾丸がナターシャに跳ね返ったことがわかりました。 どうする 銃をアイドル状態に充電しますか？ 靴を交換しますか？ 柱を取り外すことにしました。 削除して保存し、「Rzhevsky中euが死亡しました。」というメッセージを受け取ります。 もう一度、あなたは座って理解し、次の章で彼はもはやポールに傾いていることがわかります...

Haskellistsが純粋な機能をそれほど重視している理由を理解してください。 第一に、データ競合を心配することなく、努力なしで並列化されたコードを書くことができます。 次に、コンパイラーが計算を効率的に最適化できるようにします。 そして第三に、副作用がなく、純粋な関数が外部状態から独立しているため、プログラマは非常に大きなプロジェクトでも簡単にサポート、テスト、リファクタリングできます。



言い換えれば、Haskell言語の作成者は、世界の外部状態から完全に隔離された世界、つまりすべての機能がきれいで、状態がなく、すべてが不可能に最適化されており、すべてが努力なしで並列化された世界の外部状態から完全に隔離された世界を思い付きました側。 言語ではなく、夢！ Eugenio Moggi がモナドの概念に関する科学的研究でリストした「些細な事」をどうするかを理解することだけが残っています。

真空のこの非常に球形の馬で、私たちが隔離されている外の世界からだけ来るプログラムの初期データを取得するにはどうすればよいのでしょうか？ もちろん、ユーザー入力の結果を純粋な関数（たとえば、キーボードからの文字入力を受け付けるgetChar



関数）の引数として使用できますが、まず、この方法で、居心地の良いクリーンな世界に必要な「ダーティ」関数を作成します。それはそこで中断し、次に、そのような関数は常に同じ引数（ getChar



関数）を持ちますが、ユーザー（ここでは待ち伏せ！）が常に異なるキーを押すため、計算値は常に異なります。

プログラムの結果である、居心地の良い、純粋に機能的な世界から隔離された、外の世界に結果を与える方法は？ 結局、数学的な意味での関数は常に結果を返す必要があり、一部のデータを外部に送信する関数は何も返さないため、関数ではありません！

いわゆる部分的に定義された関数、つまり、すべての引数に対して定義されていない関数をどうしますか？ たとえば、よく知られている除算関数はゼロによる除算に対して定義されていません。 このような関数は、用語の数学的な意味での本格的な関数でもありません。 もちろん、そのような引数に対して例外をスローできますが、...

...しかし、例外はどうしますか？ 例外は、純粋な関数から期待される結果ではありません！

非決定的コンピューティングをどうするか？ つまり、正しい計算結果が1つではなく、多くの場合です。 たとえば、単語の翻訳を取得したい場合、プログラムはその意味のいくつかを一度に示し、それぞれが正しい結果になります。 純粋な関数は常に1つの結果のみを返す必要があります。

そして、続編をどうするか？ 継続とは、いくつかの計算を実行した後、それらが完了するのを待たずに現在の状態を保存し、他のタスクに切り替えることです。そのため、完了後に不完全な計算に戻り、中断したところから続行します。 状態がなく、ありえない純粋に機能的な世界では、どのような状態について話しているのでしょうか？

そして、最後に、どういうわけか外部状態を考慮するだけでなく、何らかの方法でそれを変更する必要がある場合、何をすべきでしょうか？

計算をクリーンに保ち、表明された問題を解決する方法を一緒に考えましょう。 そして、これらすべての問題に対して共通の解決策が見つかるかどうかを見てみましょう。

計算と「その他」

そのため、純粋な機能に精通し、その純粋さがプログラマが直面する最も複雑な問題を取り除くことができることに気付きました。 しかし、純粋な機能を活用する能力を維持するために解決しなければならない多くの問題についても説明しました。 私はそれらを再び与えます（I / Oに関連する問題を取り除きますが、これについては後で説明します）、それらの一般的なパターンを見ることができるようにそれらをいくらか再編成します：

すべての引数に対して定義されていない関数がある場合があります。 関数が定義されているこの関数に引数を渡すとき、結果を計算する必要があります。 しかし、定義されていない引数を渡す場合、関数が何か他のもの （例外、エラーメッセージ、または命令型null



類似物）を返すようにします 。

関数が結果を1つではなく、他の何か （たとえば、結果のリスト全体、またはまったく結果なし（結果の空のリスト））を与えることがあります。

関数の値を計算するために、引数だけでなく、 何か他のもの （たとえば、外部環境からのデータ、構成ファイルからの設定など）も取得したい場合があります。

次の関数を渡すために計算の結果を取得するだけでなく、 それを他の何かに引数として適用したい場合もあります（何らかの状態を取得した後、戻って計算を続行することができます。これは継続の意味です）。

計算を実行するだけでなく、 何か他のことも実行したい場合があります （たとえば、ログに何かを書き込む）。

関数を作成するときに、計算の結果だけでなく、 他の何か （たとえば、最初にどこかから読み取り、次に何らかの方法で制御された方法で変更するなど）を次の関数に渡したい場合があります 。

一般的なパターンに気づきましたか？ 擬似コードでは、次のように記述できます。

  ( /  - ) { //    / //  -  return (   / - ) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

もちろん、この「他の何か」を関数の追加引数として渡すことができます（このアプローチは命令型プログラミングで使用され、「スレッド状態」と呼ばれます）が、純粋な計算と「他の何か」一度に積み重ねることは最良のアイデアではありません。 また、これにより、説明したすべての状況に対して単一のソリューションを取得することはできません。



初めに議論され、数字を発明した古代エジプト人を思い出しましょう。 多くの羊の図を描く代わりに、彼らは計算をその文脈から分離しました 。 現代的には、コンピューティングとそのコンテキストをカプセル化しました。 そして、それらの前に量を計算する概念が私たちが考えていることと密接に関連している場合、彼らの革新はそれを2つの並行する「実行フロー」に分割しました-計算に直接接続されたストリームとそれは -つまり、計算のコンテキストです（計算中にコンテキストを保存できるだけでなく、たとえば群れの羊から何匹のケバブが得られるかを計算すると、コンテキストも変更されるためです）。







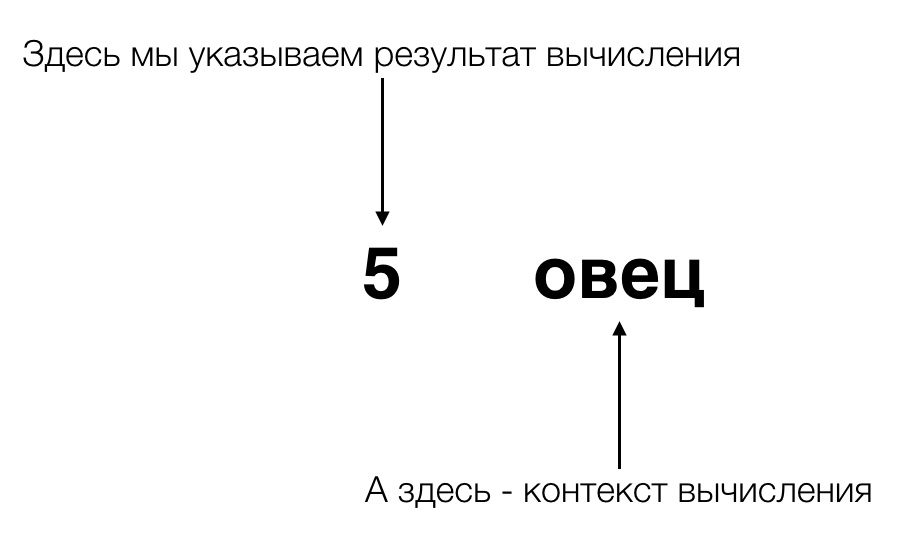
Haskellで「他の何か」を表現し、同時に最も一般化されたソリューションを取得したい場合、この「他の何か」を追加のタイプとして表現します。 ただし、単純型ではなく、他の型を引数として取る関数型です。 複雑で分かりにくいですね。 心配しないでください、それは非常に簡単で、数分後にあなた自身で見るでしょう。

「他の何か」のカプセル化

1998年12月11日、火星を研究するために火星気候オービター宇宙船が打ち上げられました。 デバイスが火星に到達した後、それは失われました。 調査後、制御プログラムでは、一部の距離がインチ単位で考慮され、他の距離はメートル単位で考慮されることが判明しました。 どちらの場合も、これらの値はDouble



型で表されていました。 関数がインチ単位でカウントした結果、メートル単位で表された引数が渡されたため、当然、計算でエラーが発生しました。



このようなエラーを回避したい場合は、メートルで表された値がインチで表​​された値と異なる必要があります。したがって、間違った単位で表された値を関数に渡そうとすると、コンパイラーがエラーを通知します。 Haskellでは、これは非常に簡単です。 2つの新しい型を宣言しましょう。

 data DistanceInMeters = Meter Double data DistanceInInches = Inch Double
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

DistanceInMeters



とDistanceInInches



はタイプコンストラクターと呼ばれ、 Meter



とInch



はデータコンストラクターと呼ばれます（タイプコンストラクターとデータコンストラクターは異なるスコープに存在するため、同じようにすることができます）。



これらの型宣言を見てください。 データコンストラクターは関数のように動作し、引数としてDouble



型の値を取り、計算の結果としてDistanceInMeters



型またはDistanceInInches



型の値を返すと思いませんか？ そうです-データコンストラクターも関数です！ そして、以前に誤ってDouble



型の値をDouble



を取る関数に渡すことができた場合、この関数では、引数にDouble



型の値だけでなく、 何か他のもの 、つまり- «» Meter



Inch



.



ただし、この場合、最も一般的なソリューションは得られませんでした。当社の機能konstruktory_dannyhの引数Meter



とInch



の型の値のみを取ることができますDouble



。これは、この特定のタスクのロジックによって決定されますが、メインタスクを解決するために-純粋なコンピューティングを「他の何か」から分離します-この「他の何か」を表現する「ラッパー」が彼らの引数を取ることができる必要がありますタイプ。また、このタスクはHaskellで非常に簡単に解決できます。Haskell組み込みタイプの1つを見てください。

 data Maybe a = Nothing | Just a
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

見て、Maybe



どんなタイプの値でも取ることができるラッパーがあります。このラッパーには、何らかの値を含めることができます（データコンストラクターを使用する場合Just



）か、何も含めることはできません（データコンストラクターを使用する場合Nothing



）。ラッパー内にデータがあるかどうかを確認するには、ラッパーMaybe



を検査するだけです。マッチ箱のようなものです。箱が空かどうかを確認するために、箱を開ける必要はありません。箱を耳に持ってきて振るだけです。Haskellは、



型Maybe



を使用して問題の1つを解決します。すべての引数に対して定義されていない純粋な関数をどう処理するかです。たとえば、関数がありますlookup



、キーとペアの連想リスト（キー、値）を渡して、このキーに関連付けられた値を見つけることができます。ただし、この関数は、渡されたキーとのペアを見つけられない場合があります。この場合、それは私たちNothing



に返され、それが見つかった場合、にラップされた値を私たちに返しJust



ます。つまり関数に定義された値を渡すと、計算の結果を（ラッパーでJust



）取得し、定義されていない値を渡すと、「何か他のもの」（Nothing



）を取得します。



しかしNothing



、だけでなく、関数が計算の結果ではなく「他の何か」を返した理由に関するメッセージも取得したい場合はどうでしょうか。問題をより明確に定義しましょう：計算が成功した場合、結果が返された場合、および失敗した場合は、エラーメッセージ、計算の結果、エラーメッセージはさまざまなタイプになります。 OK、このように書きましょう：

 data Either ab = Left a | Right b
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

型コンストラクタEither



は、型の2つの変数を受け入れることがわかります- a



およびb



（異なる型でも、同じ型でもかまいません）。計算の結果が成功した場合、それらをラッパーで取得しRight



（計算の結果はtypeになりますb



）、計算が失敗した場合、データコンストラクターのラッパーでaのエラーを取得しますLeft



。



さて、外部環境での作業はどうですか？計算の値が何らかの外部環境に依存している場合は、必要な値を計算する関数に読み込んで引数として渡す必要がありますか？述べたように、そして書いてください：

 data Reader ea = Reader (e -> a)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

計算結果が依存する環境は型変数で示されe



（型変数の代わりに必要な型に置き換えることができることを思い出してください）、計算結果の型は型変数で示されますa



。さらに、計算自体にはtypeがe -> a



あります。環境から必要な価値への機能です。



同じことが、単一の結果または他の何か（ゼロの結果または多くの結果）を返す可能性のある非決定的計算にも当てはまります。これらを追加の型でラップします。そして、あなたはおそらく知っているこのタイプ-リストのこのタイプ[a]



（のように書くことができます。この「他の何か」を表し、変数の型-当社の純計算のタイプ）。[] a



[]



a







純粋な計算の実行と並行して変更する必要がある状態であろうと、プログラムの実行中に発生する可能性がある例外であろうと、「他の何か」についても同じことを行います。私たちは、私たちで「ラップ」たちの純粋な計算のクラスでは、この「何かを」、カプセル化し、「他の何か」の処理と2つの並列ストリーム上のネットの計算を共有し、私たちが取り組んでいる、それぞれが明確に。



この時点で学んだことをまとめて要約しましょう。

純粋な関数を使用することにより、計算の並列化、コンパイラによる計算の最適化、非常に大きなプログラムでもテスト、サポート、リファクタリングの容易さに関連する大きな利点を得ることができます。

, , , «- ». , , «- », «- ».

«- », . «- » .

«- » «» , «» .

:

 a -> mb
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

m



— « », b



.

, . , - :

a -> b



, .. . ma



. ma -> mb



, , «» a -> b



m



, a -> b



, mb



.

, , first class citizens. つまり , — , .. , , , «» m



. f



, a



, , mf



ma



, « »:

 mf ` ` ma => m (f ` ` a).
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, , , , , , . f :: b -> c



g :: a -> b



, f . g



, g



, f



. f :: b -> mc



g :: a -> mb



? mb



b



— , , b



«» m



.



«» b



m



次の関数の値として渡すため。実際、純粋な計算と並行して、「ラッパー」には「他の何か」の計算があり、この計算の結果を次の関数に渡す必要もあります。一般的に、我々は機能をkompozirovatできる方法を把握する必要があるa -> mb



とb -> mc



私たちはそこから新しい機能を得ることができることa -> mc



、およびこの組成物は、我々は、「他の何か」のない計算をネット計算を失っていないしていないとき。さらに、おそらく既に推測されているように、私たちのソリューションも普遍的でなければなりません。

ファンクターは簡単ではありませんが、非常に簡単です！

したがって、3つのタスクがあります。

ラップされた値に通常の値で機能する既存の関数をどのように適用できるかを理解するため。

, , , .

, , — , , , «- », .

原則として、funktsionalschikiは怠惰な人ではなかった場合、彼らは考えimperativschikamiされているだけで包まれたデータを操作するための新機能の束を書きました。isChar :: a -> Bool



渡された値が型の値Char



であるかどうかをチェックする関数の類似物を決定するには、ラッパー型のデータコンストラクターと同じ数の方程式を記述する必要があります。たとえば、ラッパータイプMaybe a



には2つのデータコンストラクターがJust



ありNothing



ます。

 maybeIsChar :: Maybe Char -> Maybe Char -> Maybe Bool maybeIsChar (Just x) = Just (isChar x) maybeIsChar Nothing = Nothing
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのため、わざわざ（これは見た目ではありますが）せずに、ラップされたデータを操作するための各純粋関数の類似物を定義できます。そして、関数ごとにだけでなく、ラッパーごとに対応するアナログを記述する必要があります！



しかし、それは別の方法で行うことができます。既に持っている純粋な関数を最初の引数として受け取り、それをラッパーに含まれる値に適用する新しい関数を定義して、同じラッパーにラップされた新しい値を返すことができます。この関数を呼び出しますfmap



：

 fmap :: (a -> b) -> ma -> mb
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、ラッパータイプごとに通常の関数の何百もの類似物を定義する代わりに、ラッパータイプごとに関数を1つだけ定義できますfmap



。fmap



ラッパータイプの関数を定義しましょうMaybe a



：

 fmap f (Just x) = Just (fx) fmap _ Nothing = Nothing
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、ラップされた型の値にMaybe a



型関数を適用できますa -> b



。関数fmap



を1つだけ定義することで、多くの追加作業をなくすことに同意します。同じフレーズの発音は異なる場合があります。ラッパー型をMaybe a



ファンクターにしたため、多くの追加作業がなくなりました。



はい、はい！ラッパー型をファンクターにするには、関数を定義する必要がありますfmap



。これにより、通常の値で機能する関数をラッパーに「注入」できます。ファンクターは非常にシンプルだと言いました！便利です これにより、以前に定義された純粋な関数を通常だけでなく、ラップされた値でも使用できます。

適用ファンクターも非常に簡単です！

ラップされていない値で機能する関数をラップされた値に適用する方法を見つけました。しかし、関数自体もラップされている場合はどうでしょうか？ラップされた値にどのように適用しますか？



推測したと思います。ラップされた関数を最初の引数として、ラップされた値を2番目の引数としてとる関数を宣言し、そのような操作が必要なラッパータイプごとにこの関数を定義する必要があります。この関数を呼び出します<*>



（read apply; 関数の名前が​​小文字ではなく特殊文字で始まるという事実は、中置形式で使用する必要があることを示しています。通常の関数のように接頭辞形式で使用する場合は、括弧で囲む必要があります）：

 (<*>) :: m (a -> b) -> ma -> mb
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

typeに対して宣言された関数を定義しましょうMaybe a



。同時に、この型には2つのコンストラクターがあることを思い出してください。つまり、この型でラップされた関数とラップされた値は（Just



）またはNothing



：のいずれかです。

 (Just f) <*> Nothing = Nothing Nothing <*> _ = Nothing (Just f) <*> (Just x) = Just (fx)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、最初は通常の値でしか動作しなかったラップされた関数をラップされた値に適用できます（ラッパーがtypeである場合）Maybe



。他のラッパーでも同じことができるようにしたい場合、必要なのはそれらのそれぞれに対して関数を定義すること(<*>)



です。言い換えると、これらのラッパーをアプリカティブファンクタにする必要があります。関数(<*>)



とが定義されているラッパータイプはアプリカティブファンクタであるためですpure



。



関数pure



は何をしますか？ああ、ファンクターや応用ファンクターよりも簡単です！この関数pure



は通常の値を取り、それからラップされた値を作成します。彼女のタイプは次のとおりです。

 pure :: a -> ma
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

pure



ラッパー型の関数を定義Maybe



して、実際の適用可能なファンクターにします。

 pure x = Just x
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてが非常に複雑ですよね？（碑文「Sarcasm！」のプレート）



ところで、ラッパー型を適用可能なファンクターにすることで、対応する数のラップされた引数に任意の数の通常の引数を取る関数を適用できます（ファンクターは、1つの引数の通常の関数のみをラップされた値に適用できます）。これは、例えば、我々が追加できるか、であるJust 2



とJust 3



：

 pure (+) <*> Just 2 <*> Just 3 > Just 5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

あなたは笑いますが、モナドも簡単です！

そこで、（1つの引数の）通常の関数をラップされた値に適用する方法を見つけました。これを行うには、ラッパータイプの関数を定義する必要がありますfmap



。そして、この関数をラッパータイプに実装したため、ファンクターになるために必要なものは何もないため、誇らしげにファンクターと呼ばれる権利があります。



また、ラップされた値にラップされた関数を適用する方法を見つけました。これを行うには、ラッパータイプに2つの関数を定義する必要があります- pure



そして<*>



-また、これにより、任意の数の引数を取るラップされた値に通常の関数を適用できました。そして、これらの関数をラッパータイプに定義するとすぐに、アプリケーションファンクタと呼ばれる権利を獲得しました。ところで、ラッパー型を適用可能なファンクターにするためには、最初に通常のファンクターにする必要があります（そして、チートすることはできません-コンパイラーはこれに従います）。これには論理的な（そして、いつものように、簡単な）説明があります。この記事はすでに非常に膨れ上がっているので、あなた自身で勉強するために残しておきます。



それは、我々は2つの機能の構図を作ることができる方法を理解するために私たちのために残っているa -> mb



、とb -> mc



そのため、純粋な計算の結果と、ラッパーに含まれる「他の何か」を計算した結果の両方が、最初の関数から2番目の関数に転送されます。おそらく既に推測されているように、このためには、ラッパータイプに対して1つまたは2つの関数を定義する必要があります。そして、最も独創的な人は、これらの関数が定義されるラッパー型がモナドと呼ばれることをすでに理解しています。



これらの関数の最初は関数return



です。return



関数からの出口点を定義することは必須ではありません。 Haskell関数return



は通常の値を取り、それからラップされた値を作成します。

 return :: a -> ma
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

pure



ラッパー型を適用可能なファンクターに変えた章の関数のように聞こえますか？つまり、これらの関数は同じ仕事をします。そして、モナドを作成したいラッパー型は、最初に適用可能なファンクター（そしてその前に-単なるファンクター）にならなければならないというルールがあります。つまり、このラッパー型に対して、すでに純粋関数return



を定義しているので、関数を非常に定義できますシンプル：

 return = pure
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ラッパー型をモナドにするために定義する必要がある2番目の関数が呼び出されます(>>=)



（読み取りバインド）。次のタイプがあります。

 (>>=) :: mb -> (b -> mc) -> mc
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

うーん...それは実際に機能の構成に似ていない何か。そうです。関数(>>=)



はラップされた値とtype の関数を受け取り、a -> mb



タイプラッパーでラップされた純粋な計算の結果と「何か」を計算した結果（またはこれを保存した結果）の両方をこの関数に渡す方法を決定する必要がありますラッパー自体に含まれる「計算」が行われなかった場合は「その他」。つまりこの場合、関数を表示せずa -> mb



、その結果として型の値を取得しましたmb



。つまり、すでにどこかにあるということです。ただし、この関数を使用して、構成関数を少し後で定義します(>>=)



。それまでの間、それをしてください。ラッパーのtypeを



実装(>>=)



しましょうMaybe



。彼には2つのデータコンストラクターがあるため、これには2つの方程式が必要です。「arrow to Leysley」という名前から、b -> mc



文字のような関数を呼び出しましょう（通常の値を取り、ラップされた値を返す関数はすべて「Claysley Arrows」と呼ばれ、以前に実装した関数も「Claysley Arrow」です）：k



return

 —       Nothing,   Nothing Nothing >>= _ = Nothing —       ,    ""    k (Just x) >>= k = kx
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以上です。ラッパー型Maybe



はモナドになりました！これをするためにしなければならなかったことは、機能return



とそれを決定すること(>>=)



でした。



（純粋な機能を提供し、保持した利点に加えて）それは私たちに何を与えましたか？意味を伝えたいクライズリーの矢印のコンベヤー全体を想像してください。これらの各Claysley矢印はMaybe



、データコンストラクターを使用してラッパーにラップされた値Just



、またはNothing



。明らかに、このチェーンからのある種のKleisley矢印がを与えたNothing



場合、この値をパイプラインに沿ってさらに渡すことは意味がありません。それで、私たちは何をしますか？各矢印の操作後、クレイズリーは助けを借りてチェックしif then else



、前の関数を返しませんでしたNothing



か？



皇帝はまさにそれを行い、多くのネストされた構造からstructuresい構造を構築しますif then else



。しかし、(>>=)



このような錫なしでこの問題を解決する関数を定義しました。自分で確認してください：どこかNothing



に現れた場合、演算子は(>>=)



関数に渡さずにパイプラインの最後まで単純に「ストレッチ」します。したがって、nullの チェックを心配することなく、計算チェーンを作成できますNothing



。モナドを使用すると、純粋な関数を使用する利点を維持できるだけでなく、コードをはるかに少なく記述でき、コード自体がはるかに読みやすくなります。

そして、さらにいくつかのモナドを定義しましょう

もう1つのモナドを定義しましょうか？型Either ab



よりもエラーと例外をより明確に処理できるラッパー型を使用しますMaybe



。このタイプの定義を思い出してみましょう。

 data Either ab = Left a | Right b
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

-このタイプは2つのコンストラクタ、のいずれかを持っているLeft



-入力するように設定されているa



-これは我々がラッパーであるエラーメッセージに使用することのタイプは、このように「他の何か」されている、第二は、 - Right



-タイプに設定されていますb



-これが「基本的な」計算のタイプです。 「基本的な」計算が過剰に行われない場合、計算の値はClaysley矢印の構成のチェーンに沿ってデータコンストラクターでラップされRight



ます。そして、エラーが発生するとすぐに-データコンストラクターを使用してラップされた結果のメッセージを取得しますLeft



。



最初に関数を定義しますreturn



：

 return x = Right x
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここではすべてが明らかです。return



エラーメッセージを関数に渡すのではなく、何らかの型の値b



を渡すため、データコンストラクタ関数をこの値に適用しRight



て型の値を取得しますEither ab



。



ここで、演算子を定義します(>>=)



。ここでのロジックはモナドと同じMaybe



です：チェーンに沿ってタイプ値が渡される少なくとも1つのKleisley矢印Either ab



が、データコンストラクター関数Left



でラップされたエラーメッセージを表示する場合、計算チェーン全体の結果はこのエラーメッセージになります。すべての計算が成功した場合（つまり、各Claysley矢印がdata_constructor関数を使用してラップされた計算の結果を返した場合）Right



）、次の各機能をこの結果に適用する必要があります。

 (Left x) >>= _ = Left x (Right x) >>= k = kx
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

モナドMaybe



などEither



。どちらにも2つのデータコンストラクターがあり、そのうちの1つは計算の失敗を示します（したがって、次の関数に渡さずに、クレイズリーの矢印でコンポジションの最後に「ドラッグ」する必要があります）。両方のモナドの2番目のデータコンストラクターは、計算が正常に完了したことを意味し、これらの計算の値は次のKleisley矢印に渡されます。



それでは、以前に実装されたモナドとは異なるモナド、リストモナドを実装しましょう。リストモナドのClaysley矢印のタイプはa -> [b]



です。演算子の最初の引数(>>=)



はラップされた型の値ですma



。この場合、これは[a]



（型の値のリストa



）です。さらに、リストは空の場合もあれば、タイプの1つ以上の値を含む場合もありますa



。



この場合、Claysley矢印を値のリストに適用するとはどういう意味ですか？これは、リストの各値に適用する必要があることを意味します。空のリストの場合、すべてが明確です。Claysley矢印を使用するものは何もないので、結果として空のリストを取得します。空でないリストの各値に対して、関数を使用してClaysley矢印を適用できますfmap



（リストからモナドを作成するため、これはリストがファンクターでもあることを意味します-覚えていますか？）。ただし、functionのタイプを思い出してみましょう。fmap



便宜上、抽象ラッパータイプm



を特定のラッパーリストタイプに置き換えます。

 fmap :: (a -> b) -> [a] -> [b]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、渡されfmap



た関数のタイプをClaysley矢印のタイプに置き換えます。

 fmap :: (a -> [b]) -> [a] -> [[b]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Kleisley矢印を渡した結果fmap



、type mb



ではなくtypeの値を取得することがわかりますmmb



。二重にラップします。これはoperatorのタイプに対応しない(>>=)



ため、ラッパーの1つを「削除」する必要があります。これを行うにconcat



は、リストのリストを受け入れ、内部リストを連結し、通常の値のリストを返す関数があります。これで(>>=)



リストモナドの演算子を定義する準備ができました：

 [] >>= _ = [] xs >>= k = (concat . fmap k) xs
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

演算子を決定するロジックは(>>=)



、すべての場合で同じであることがわかります。ラップされた各値には、計算の結果と「他の何か」があり、別の関数に渡すときに計算とこの「他の何か」で何をする必要があるかを考えます。 「その他」は、計算の成功または失敗のマーカー、計算の成功またはエラーメッセージのマーカー、計算がゼロから無限の結果を返すことができるマーカーの場合があります。 「他の何か」はログエントリ、つまり読み取り、「基本」計算の引数として渡す状態にすることができます。または、「基本」計算と並行して、読み取り、変更、および別の関数に渡された状態を再度変更します。



モナドには複雑なものは何もないことを認めなければなりません（ファンクターや応用ファンクターのように）。モナドは、2つの関数が定義されている単なるラッパータイプです- return



と(>>=)



。



ただし、(>>=)



ステートフルラッパーの定義はやや複雑です。それらの実装には、この記事で紹介したものよりもHaskellの構文に精通している必要があるため、ここでは紹介しません。しかし、私はあなたを安心させたいです。第一に、非常に高度なHaskellプログラマーでさえ、通常はモナドを作成せず、組み込み言語を使用します。これは、あらゆる場合に十分です。第二に、モナド（状態で動作するものを含む）を使用することは、モナドを定義するよりもはるかに簡単です。これについては、次の章で説明します。



モナドを理解するには、単純な原則を理解する必要があります。「基本的な」計算と、並行して発生する「他の何か」の計算があります。また、「クレイズリーシューター」の「コンベア」でこれらの計算がどの程度正確に行われるかは、オペレーターが決定し(>>=)



ます。したがって、演算子を自分(>>=)



で定義する必要はほとんどありませんが、そこに何がどのように発生するかをよりよく理解するために、さまざまな組み込みモナド型に対して定義される方法を理解することは非常に役立ちます。



ちなみに、演算子(>>=)



がクレイズリーの矢印の合成の切り捨てられたバージョンであると言ったとき、私はそれを通して実際の合成を決定することを約束しました。これはHaskell言語の標準関数であり、と表示され(>=>)



、「魚」（「魚演算子」）と発音されます。

 (>=>) :: (a -> mb) -> (b -> mc) -> a -> mc (f >=> g) x = fx >>= g
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

x



私たちが持っているタイプはvalue a



でf



あり、g



Kleisleyの矢印です。 Claysley矢印f



をvalue x



に適用すると、ラップされた値が取得されます。そして、覚えているように、ラップされた値をClaysleyの次の矢印に転送する方法は、オペレーターが知ってい(>>=)



ます。



次のパートでは、Haskell言語で定義されたモナドを使用する方法を見ていきます（そして、大多数のプログラマーは他のモナドを必要としません）。Writer



（ログエントリの「他の何か」で表現されている）、モノイドとは何か、なぜモノイドが必要なのかを説明する正当な理由があります。そして、「タイプクラス」と呼ばれるもう1つの強力なHaskellメカニズムについて説明し、すでにお会いしたファンクター、応用ファンクター、モナドが、モノイドやタイプクラスとどのように結び付いているかを説明して、話を終わります。まだ伝えていません。そして最後に、私は約束を果たし、通常のモナドとは異なるI / Oモナドについて簡単に話します（ただし、実装のみが異なり、使用中は他のモナドと同じくらい簡単です）。