Clever Geek Handbook

電卓で1°の罪

重要な明確化-電卓は、 sinボタンなしで正常です。 会計や市場でのように。



カシオ計算機



カットの下には、冷戦時代の古代サマルカンドからアメリカまで、さまざまな時代の3つの異なる解決策があります。



シンプルなソリューション



最初に思い浮かぶのは、この呪文です：



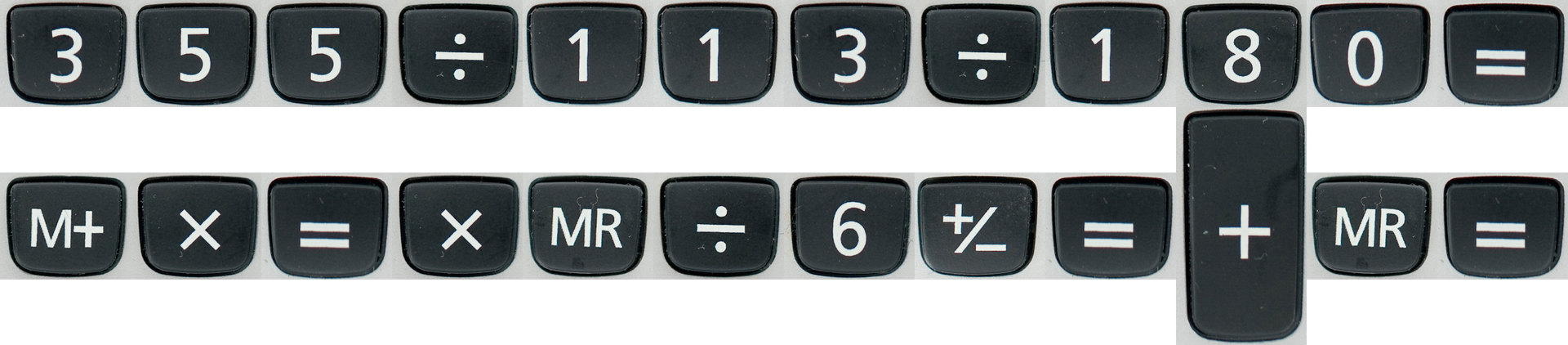
355/113/180 = MC M + * = * MR / 6 +-= + MR =



電卓のこのわかりにくいスコアを、よりわかりやすい言語bcに変換します。 多くの場合、UNIXライクなオペレーティングシステムのコマンドラインで計算機として使用されます。 次のようなものが表示されます。 



scale = 7 x = 355/113/180 xx^3/6 .0174524


どこから来たの
サインをゼロに近い行に展開し、この行の最初の数人のメンバーを取得して、1度置換します。 この場合、角度は小さいため、3次の多項式に制限できます。



sin（x）≅x-x 3/6



置換する前に、度をπ



で乗算し、180°で除算してラジアンに変換する必要があります。



別の賞品は、奇妙な数字355と113によって気付かれることになっています。これらは、中国の友人Zu Chunzhi（祖沖之）で、Q王朝（479-502）の間にさえ発見されました。 355/113比は、有理数π



数π



唯一の近似値であり、同様の精度の10進表現よりも短くなっています。




興味深いソリューション



上記の有名なトリックは、1715年にのみ登場しました。 それにもかかわらず、三角関数の値はずっと早く、はるかに正確に知られていました。



サマルカンド天文台の長、Giyas ad-din Jamshid ibn Masoud al-Kashi（غیاثالدینجمشیدکاشانی）は、1429年以前の16桁まで正確な三角関数の表を編集しました。 ペルシャ語から紀元前に翻訳すると、私たちの仕事に関する彼の呪文は次のようになりました。 



  scale = 16 sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45 sin75 = sin30*cos45+cos30*sin45 cos75 = sqrt(1-sin75^2) cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2) sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2) (sin3 = sin75*cos72-cos75*sin72) .0523359562429430 (x = sin3/3) .0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831


加算、減算、乗算、除算、平方根のみを使用していることに注意してください。 必要に応じて、これらのすべての操作は、一般に列の紙の上で実行できます。 以前は、学校で教えて、列の平方根を数えました。 これは退屈ですが、それほど難しくはありません。



このシャーマニズムとは
アル・カシの魔法のステップを取りましょう。 



  sin30 = .5 cos30 = sqrt(3)/2 sin45 = sqrt(2)/2 cos45 = sin45


30°と45°のサインとコサインは古代ギリシャ人に知られていました。 



  sin75 = sin30*cos45+cos30*sin45


30°と45°の角度の合計のサインがあります。 アル・カシの前でさえ、この式は別のペルシャの天文学者、アブル・ワファ・ムハンマド・イブン・ムハンマド・イブン・ヤハヤ・イブン・イスマイル・イブン・アッバス・アル・ブジャニによって導き出されました。 



  cos75 = sqrt(1-sin75^2)


ピタゴラスのズボンはすべての方向で同等です。 



  cos36 = (1+sqrt(5))/4 sin36 = sqrt(1-cos36^2)


これは、古代ギリシア人にも知られている正五角形のものです。 



  sin72 = 2*sin36*cos36 cos72 = sqrt(1-sin72^2)


合計のサインとピタゴラスの定理。 



  (sin3 = sin75*cos72-cos75*sin72) .0523359562429430


75°と72°の差のサインを考慮し、3°のサインを取得します。



これで3°を1°の3つの角度の合計に分解できますが、問題があります。3次方程式が得られます。



sin 3°= 3 x-4 x 3



ここで、x = sin 1°。 3次方程式を解析的に解く方法は誰も知りませんでした。



Wise al-Kashiは、この方程式は次の形式で表現できることに注意しました。



f（x）=（sin 3°+ 4 x 3 ）/ 3



そして、 単純な反復法をf（x）に適用します。 私は当時、ニュートンもラフソンもまだ生まれていなかったことを思い出します。 



  (x = sin3/3)


最初の近似。 



  .0174453187476476 (x = (sin3+4*x^3)/3) .0174523978055315 (x = (sin3+4*x^3)/3) .0174524064267667 (x = (sin3+4*x^3)/3) .0174524064372703 (x = (sin3+4*x^3)/3) .0174524064372831 (x = (sin3+4*x^3)/3) .0174524064372831


5回の反復後、16文字を取得します。





計算機自体によると



好奇心reader盛な読者には正当な質問があるかもしれません。そのようなボタンを持つ計算機はどのようにサイン値を計算しますか？



ほとんどの計算機は、冷戦中に米軍産業複合体の腸内で生まれた、完全に3番目の方法である「 桁ごと」を使用することがわかりました。



そして、ここでB-58爆撃機
このアルゴリズムはJack Walderによって発明されました。JackWalderは、Convairで前述の爆撃機のナビゲーションコンピューターで働いていました。



桁ごとの方法の主な利点は、2つの操作による加算と除算のみを使用することです（右にシフトすることで簡単に実装できます）。



さらに、アルゴリズムは、ほとんどの計算機で使用されているバイナリ10進コードで直接動作するように作成できますが、以下の例では、このジャングルを使用しません。



このアルゴリズムは反復的であり、反復ごとに1つのアークタンジェントテーブルを使用します。 テーブルは事前に計算する必要があります。 



 #include <stdio.h> #include <math.h> int main(int argc, char **argv) { int bits = 32; int cordic_one = 1 << (bits - 2); printf("//    ,     \n"); printf("static const int cordic_one = 0x%08x;\n", cordic_one); printf("static const int cordic_table[] = {\n"); double k = 1; for (int i = 0; i < bits; i++) { printf("0x%08x, // 0x%08x * atan(1/%.0f) \n", (int)(atan(pow(2, -i)) * cordic_one), cordic_one, pow(2, i)); k /= sqrt(1 + pow(2, -2 * i)); } printf("};\n"); printf("static const int cordic_k = 0x%08x; // %.16f * 0x%08x\n", (int)(k * cordic_one), k, cordic_one); }


同時に、スケーリング係数cordic_k



が考慮されます。



その後、悪名高いsin 1°は次のように計算できます。 



 #include <stdio.h> #include <math.h> //    ,      static const int cordic_one = 0x40000000; static const int cordic_table[] = { 0x3243f6a8, // 0x40000000 * atan(1/1) 0x1dac6705, // 0x40000000 * atan(1/2) 0x0fadbafc, // 0x40000000 * atan(1/4) 0x07f56ea6, // 0x40000000 * atan(1/8) 0x03feab76, // 0x40000000 * atan(1/16) 0x01ffd55b, // 0x40000000 * atan(1/32) 0x00fffaaa, // 0x40000000 * atan(1/64) 0x007fff55, // 0x40000000 * atan(1/128) 0x003fffea, // 0x40000000 * atan(1/256) 0x001ffffd, // 0x40000000 * atan(1/512) 0x000fffff, // 0x40000000 * atan(1/1024) 0x0007ffff, // 0x40000000 * atan(1/2048) 0x0003ffff, // 0x40000000 * atan(1/4096) 0x0001ffff, // 0x40000000 * atan(1/8192) 0x0000ffff, // 0x40000000 * atan(1/16384) 0x00007fff, // 0x40000000 * atan(1/32768) 0x00003fff, // 0x40000000 * atan(1/65536) 0x00001fff, // 0x40000000 * atan(1/131072) 0x00000fff, // 0x40000000 * atan(1/262144) 0x000007ff, // 0x40000000 * atan(1/524288) 0x000003ff, // 0x40000000 * atan(1/1048576) 0x000001ff, // 0x40000000 * atan(1/2097152) 0x000000ff, // 0x40000000 * atan(1/4194304) 0x0000007f, // 0x40000000 * atan(1/8388608) 0x0000003f, // 0x40000000 * atan(1/16777216) 0x0000001f, // 0x40000000 * atan(1/33554432) 0x0000000f, // 0x40000000 * atan(1/67108864) 0x00000008, // 0x40000000 * atan(1/134217728) 0x00000004, // 0x40000000 * atan(1/268435456) 0x00000002, // 0x40000000 * atan(1/536870912) 0x00000001, // 0x40000000 * atan(1/1073741824) 0x00000000, // 0x40000000 * atan(1/2147483648) }; static const int cordic_k = 0x26dd3b6a; // 0.6072529350088813 * 0x40000000 void cordic(int theta, int& s, int& c) { c = cordic_k; s = 0; for (int k = 0; k < 32; ++k) { int d = (theta >= 0) ? 0 : -1; int tx = c - (((s >> k) ^ d) - d); int ty = s + (((c >> k) ^ d) - d); c = tx; s = ty; theta -= ((cordic_table[k] ^ d) - d); } } int main(void) { double alpha = M_PI / 180; int sine, cosine; cordic(alpha * cordic_one, sine, cosine); printf("CORDIC: %.8f\nExpected: %.8f\n", (double)sine / cordic_one, sin(alpha)); }


結果： 

 CORDIC: 0.01745240 Expected: 0.01745241


32回の反復があるため、小さなエラーが残ります。 計算機は通常40回の反復を使用します。





More articles:


All Articles