現在、 ANSYS 、 Abaqus 、 Patran 、 Cosmosなど、さまざまなソフトウェアパッケージがあります。 これらのソフトウェアパッケージを使用すると、構造力学、流体力学、熱力学、電気力学などの多くの問題を解決できます。 原則として、メソッド自体の実装は非常に複雑で膨大なものと見なされます。
ここで、現時点では、最新のツールを使用して、2次元の平面応力状態の問題に対して最も簡単なFEM電卓をゼロから作成することは、それほど複雑で面倒ではないことを示したいと思います。 この種のタスクを選んだのは、有限要素法を適用した最初の成功例だったからです。 そしてもちろん、最も簡単に実装できます。 以下に示すように、これは数値積分を必要としない唯一のフラット要素であるため、線形の3ノード要素を使用します。 統合操作(完全に簡単なわけではありませんが、その実装は非常に興味深い)を除いて、高次の要素については、考え方はまったく同じです。
注目を集める画像:
歴史的に、FEMの最初の実用的な応用は力学の分野であり、用語とメソッドの最初の解釈に大きな影響を与えました。 最も単純な場合、この方法の本質は次のように説明できます。連続媒体は同等のヒンジシステムに置き換えられ、静的に不確定なシステムの解決策はよく知られ、研究されている力学の問題です。 この単純化された工学的解釈は、この方法の普及に貢献しましたが、厳密に言えば、このような方法の理解は正しくありません。 メソッドの正確な数学的正当化は、メソッドの最初の成功したアプリケーションよりもずっと後に与えられましたが、これにより、力学の分野だけでなく、より広範な問題の範囲を拡大することができました。
メソッドの詳細については説明しませんが、それに関する多くの文献がありますが、代わりにメソッドの実装に焦点を当てます。 メカニックの最小限の知識、または同じソプロマットが必要です。 また、少なくともアイデアが明確であったかどうかに関係なく、メカニックに関係のない人々のレビューも喜んでいます。 このメソッドはC ++で実装されますが、この言語の特定の機能は使用せず、この言語を知らない人にもコードが理解できることを望みます。
これはメソッドの実装の一例にすぎないため、すべてを複雑にせず、理解するためにすべてを最も単純な形のままにしておくために、多くのプログラミング原則を損なうよりも簡潔にしたいと思います。 これは、優れた保守可能な信頼できるコードを記述する例ではなく、FEMを実装する例です。 したがって、主な目標に集中するために多くの簡略化があります。
入力データ
メソッド自体を開始する前に、入力データをどの形式で表示するかを確認しましょう。 問題のオブジェクトは、多数の小さな要素、この場合は三角形に分割する必要があります。 したがって、連続媒体を、グリッドを形成するノードと有限要素のセットで置き換えます。 以下の図は、番号付きのノードと要素を持つグリッドの例を示しています。
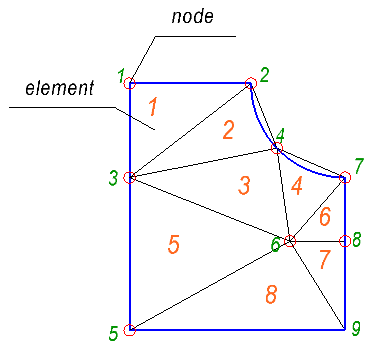
図では、9つのノードと8つの要素が表示されています。 グリッドを説明するには、2つのリストが必要です。
- 各ノードの座標を定義するノードのリスト。
- アイテムのリスト。
要素のリストでは、各要素は要素が形成するノードのインデックスのセットによって決定されます。 私たちの場合、三角形の要素しか持っていないため、各要素に使用するインデックスは3つだけです。
例として、上記のグリッドの場合、次のリストがあります。
ノードのリスト:
0.000000 31.500000 15.516667 31.500000 0.000000 19.489759 18.804134 23.248226 0.000000 0.000000 20.479981 11.365822 27.516667 19.500000 27.516667 11.365822 27.516667 0.000000
アイテムのリスト:
1 3 2 2 3 4 4 6 7 4 3 6 7 6 8 3 5 6 6 5 9 6 9 8
同じ要素を指定するにはいくつかの方法があることに注意してください。 ノードインデックスは、時計回りまたは反時計回りにリストできます。 通常、反時計回りの列挙が使用されるため、すべての要素がこの方法で指定されると想定します。
タスクの完全な説明を含む入力ファイルを作成しましょう。 混乱を避けて複雑にしないために、C / C ++配列ではゼロからインデックスが作成されるため、1からではなく0から始まるインデックスを使用することをお勧めします。 最初のテスト入力ファイルでは、可能な限り単純なグリッドを作成します。
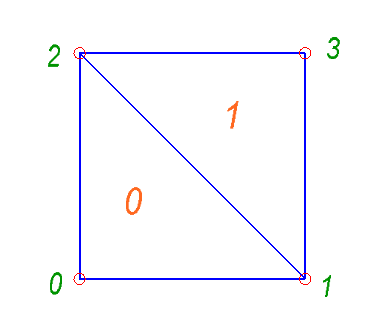
最初の行を材料特性の説明にします。 たとえば、鋼の場合、ポアソン比ν= 0.3およびヤング率E = 2000 MPa:
0.3 2000
次に、ノードの数とノードのリスト自体の行が続きます。
4 0.0 0.0 1.0 0.0 0.0 1.0 1.0 1.0
次に、要素の数、要素のリストを含む行が続きます。
2 0 1 2 1 3 2
ここで、バインディング、または彼らが言うように、第1種の境界の条件を設定する必要があります。 このような境界条件として、ノードの動きを修正します。 軸に沿った動きを互いに独立して修正できます。 x軸またはy軸に沿った移動、またはその両方を一度に禁止できます。 一般的な場合、特定の初期変位を指定できますが、ゼロ初期変位のみに制限します。 したがって、特定のタイプの移動制限を持つノードのリストが作成されます。 制限の種類は番号で示されます。
- 1-x軸方向の移動は禁止されています
- 2-y軸の方向への移動は禁止されています
- 3-x方向とy方向の両方に移動することは禁止されています
最初の行は、制限の数を定義します。
2 0 3 1 2
次に、負荷を設定する必要があります。 ノーダルフォースでのみ動作します。 厳密に言えば、節点の力は言葉の一般的な意味での力と見なされるべきではありません。これについては後で説明しますが、ノードに作用する力と考えてみましょう。 ノードインデックスと対応する力ベクトルのリストが必要です。 最初の行は、適用される力の量を決定します。
2 2 0.0 1.0 3 0.0 1.0
検討中の問題は、底面が固定され、上面に張力が作用する正方形のボディであることが容易にわかります。

入力ファイル全体:
0.3 2000 4 0.0 0.0 1.0 0.0 0.0 1.0 1.0 1.0 2 0 1 2 1 3 2 2 0 3 1 2 2 2 0.0 1.0 3 0.0 1.0
Eigen-数学ライブラリ
コードを書き始める前に、数学ライブラリEigenについてお話したいと思います。 非常にクリーンで表現力豊かなAPIを備えた、成熟した信頼性の高い効率的なライブラリです。 多くのコンパイル時最適化があり、ライブラリは明示的なベクトル化を実行でき、SSE 2/3/4、ARMおよびNEON命令をサポートします。 私に関して言えば、このライブラリは、簡潔で表現力豊かな方法で複雑な数学計算を実装できるという理由だけで注目に値します。
後で使用するEigen APIの一部について簡単に説明します。 このライブラリに精通している読者は、このセクションをスキップできます。
行列には、密と疎の2種類があります。 両方のタイプを使用します。 密行列の場合、すべての要素はインデックスの順序でメモリ内にあり、列優先(デフォルト)と生優先の両方の配置がサポートされます。 このタイプの行列は、比較的小さい行列またはゼロ要素の数が少ない行列に適しています。 スパース行列は、少数の非ゼロ要素を持つ大きな行列を格納するのに適しています。 グローバル剛性マトリックスにスパースマトリックスを使用します。
密行列
密行列を使用するには、 <Eigen / Dense>ヘッダーを含める必要があります。 密行列には、固定と動的の2つの主なタイプがあります。 固定サイズのマトリックスは、コンパイル時にサイズがわかっているマトリックスです。 動的サイズのマトリックスの場合、そのサイズはコード実行の段階で設定でき、さらに動的マトリックスのサイズはその場で変更することさえできます。 もちろん、可能な限り固定サイズの行列を優先する必要があります。 動的行列のメモリはヒープに割り当てられ、未知の行列サイズはコンパイラが実行できる最適化を制限します。 固定マトリックスをスタックに割り当てることができ、コンパイラーはループなどをデプロイできます。 行列の行数が固定されているが、列の数が動的である場合、またはその逆の場合、混合型も可能です。
固定サイズの行列は、次のように定義できます。
Eigen::Matrix<float, 3, 3> m;
ここで、mは3×3の固定サイズの浮動小数点行列です。次の定義済みの型も使用できます。
Eigen::Matrix2i Eigen::Matrix3i Eigen::Matrix4i Eigen::Matrix2f Eigen::Matrix3f Eigen::Matrix4f Eigen::Matrix2d Eigen::Matrix3d Eigen::Matrix4d
さらにいくつかの定義済みのタイプがあります;これらは基本的なものです。 数値は正方行列の次元を示し、文字は行列要素のタイプを示します。iは整数、fは単精度浮動小数点数、dは倍精度浮動小数点数です。
ベクトルの場合、個別のタイプはありません。ベクトルは同じ行列です。 列ベクトル(文献で行ベクトルが見つかる場合があるため、明確にする必要があります)は、次のように宣言できます。
Eigen::Matrix<float, 3, 1> v;
または、事前定義されたタイプのいずれかを使用できます(表記はマトリックスの場合と同じです)。
Eigen::Vector2i Eigen::Vector3i Eigen::Vector4i Eigen::Vector2f Eigen::Vector3f Eigen::Vector4f Eigen::Vector2d Eigen::Vector3d Eigen::Vector4d
クイックリファレンスとして、次の例を作成しました。
#include <iostream> int main() { //Fixed size 3x3 matrix of floats Eigen::Matrix3f A; A << 1, 0, 1, 2, 5, 0, 1, 1, 2; std::cout << "Matrix A:" << std::endl << A << std::endl; //Access to matrix element [1, 1]: std::cout << "A[1, 1]:" << std::endl << A(1, 1) << std::endl; //Fixed size 3 vector of floats Eigen::Vector3f B; B << 1, 0, 1; std::cout << "Vector B:" << std::endl << B << std::endl; //Access to vector element [1]: std::cout << "B[1]:" << std::endl << B(1) << std::endl; //Multiplication of vector and matrix Eigen::Vector3f C = A * B; std::cout << "C = A * B:" << std::endl << C << std::endl; //Dynamic size matrix of floats Eigen::MatrixXf D; D.resize(3, 3); //Let matrix D be an identity matrix: D.setIdentity(); std::cout << "Matrix D:" << std::endl << D << std::endl; //Multiplication of matrix and matrix Eigen::MatrixXf E = A * D; std::cout << "E = A * D:" << std::endl << E << std::endl; return 0; }
結論:
Matrix A: 1 0 1 2 5 0 1 1 2 A[1, 1]: 5 Vector B: 1 0 1 B[1]: 0 C = A * B: 2 2 3 Matrix D: 1 0 0 0 1 0 0 0 1 E = A * D: 1 0 1 2 5 0 1 1 2
詳細については、 ドキュメントを参照することをお勧めします 。
スパース行列
スパース行列は、もう少し複雑なタイプの行列です。 基本的な考え方は、マトリックス全体をそのままメモリに保存するのではなく、ゼロ以外の要素のみを保存することです。 実際の問題では、多くの場合、少数の非ゼロ要素を持つ大きな行列があります。 FEMモデルでグローバル剛性マトリックスを組み立てる場合、非ゼロ要素の数は、要素の総数の0.1%未満になる場合があります。
最新のFEMパッケージでは、非常に一般的な最新のPCで数十万ノードの問題を解決することは問題ではありません。 グローバル剛性マトリックスにストレージスペースを割り当てようとすると、次の問題が発生します。
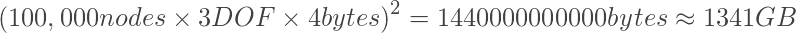
マトリックスを保存するために必要なメモリサイズは膨大です! スパース行列は、10,000倍少ないメモリを必要とします。
スパース行列は、ゼロ以外の要素のみを格納するため、メモリをより効率的に使用します。 スパース行列は、圧縮と非圧縮の2つの方法で表現できます。 非圧縮形式では、行列に要素を簡単に追加または削除できますが、このタイプの表現はメモリ使用量の観点から最適ではありません。 Eigenは、スパースマトリックスで作業する場合、一種の圧縮表現を使用します。これは、要素の動的な追加/削除に対してわずかに最適化されています。 Eigenは、このような行列を圧縮形式に変換する方法も知っています。さらに、透過的に行います。明示的に行う必要はありません。 ほとんどのアルゴリズムでは、圧縮形式のマトリックスが必要であり、これらのアルゴリズムのいずれかを使用すると、マトリックスが自動的に圧縮形式に変換されます。 逆に、要素を追加/削除すると、マトリックスは自動的に最適化された表現に変換されます。
マトリックスはどのように定義できますか? これを行う良い方法は、いわゆるトリプレットを使用することです。 これはデータ構造であり、これはテンプレートクラスです。テンプレートクラスは、マトリックス内の位置を決定するインデックスと組み合わせた1つのマトリックス要素です。 トリプレットベクトルからスパース行列を直接指定できます。
たとえば、次のスパース行列があります。
0 3 0 0 0 22 0 0 0 0 0 5 0 1 0 0 0 0 0 0 0 0 14 0 8
最初に行う必要があるのは、適切なEigenライブラリヘッダー<Eigen / Sparse>を含めることです。 次に、空のスパース5x5行列を宣言します。 次に、 トリプレットベクトルを定義し、値を入力します。 トリプレットコンストラクターは、i-index、j-index、valueの引数を受け入れます。
#include <Eigen/Sparse> #include <iostream> int main() { Eigen::SparseMatrix<int> A(5, 5); std::vector< Eigen::Triplet<int> > triplets; triplets.push_back(Eigen::Triplet<int>(0, 1, 3)); triplets.push_back(Eigen::Triplet<int>(1, 0, 22)); triplets.push_back(Eigen::Triplet<int>(2, 1, 5)); triplets.push_back(Eigen::Triplet<int>(2, 3, 1)); triplets.push_back(Eigen::Triplet<int>(4, 2, 14)); triplets.push_back(Eigen::Triplet<int>(4, 4, 8)); A.setFromTriplets(triplets.begin(), triplets.end()); A.insert(0, 0); std::cout << A; A.makeCompressed(); std::cout << std::endl << A; }
結論は次のとおりです。
Nonzero entries: (0,0) (22,1) (_,_) (3,0) (5,2) (_,_) (_,_) (14,4) (_,_) (_,_) (1,2) (_,_) (_,_) (8,4) (_,_) (_,_) Outer pointers: 0 3 7 10 13 $ Inner non zeros: 2 2 1 1 1 $ 0 3 0 0 0 22 0 0 0 0 0 5 0 1 0 0 0 0 0 0 0 0 14 0 8 Nonzero entries: (0,0) (22,1) (3,0) (5,2) (14,4) (1,2) (8,4) Outer pointers: 0 2 4 5 6 $ 0 3 0 0 0 22 0 0 0 0 0 5 0 1 0 0 0 0 0 0 0 0 14 0 8
データ構造
入力ファイルから読み込むデータと中間データを保存するには、構造を宣言する必要があります。 有限要素を記述する最も単純なデータ構造を以下に示します。 有限要素を構成するノードのインデックスと行列Bを格納する3つの要素の配列で構成されます。この行列は勾配行列と呼ばれ、後で戻ります。 CalculateStiffnessMatrixメソッドについても後述します。
struct Element { void CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets); Eigen::Matrix<float, 3, 6> B; int nodesIds[3]; };
必要なもう1つの単純な構造は、バインディングを記述するための構造です。 これは、制限のタイプを定義する列挙型と、制限が課されるノードのインデックスで構成される単純な構造です。
struct Constraint { enum Type { UX = 1 << 0, UY = 1 << 1, UXY = UX | UY }; int node; Type type; };
物事を単純にするために、いくつかのグローバル変数を定義しましょう。 グローバルオブジェクトを作成することは常に悪い考えですが、この例では完全に受け入れられます。 次のグローバル変数が必要です。
- ノード数
- X座標ノードを持つベクトル
- ノードのy座標を持つベクトル
- 要素ベクトル
- ピンベクトル
- 荷重ベクトル
コードでは、次のように定義します。
int nodesCount; int noadsCount; Eigen::VectorXf nodesX; Eigen::VectorXf nodesY; Eigen::VectorXf loads; std::vector< Element > elements; std::vector< Constraint > constraints;
入力ファイルの読み取り
何かを読む前に、どこで出力を読み、どこに書き込むかを知る必要があります。 メイン関数の最初で、入力引数の数を確認します。最初の引数は常に実行可能ファイルへのパスであることに注意してください。 したがって、3つの引数が必要です。2つ目は入力ファイルへのパス、3つ目は出力ファイルへのパスとします。 入力/出力を使用する場合、特定のケースでは、標準ライブラリのファイルストリームを使用するのが最も便利です。
最初に行うことは、入力/出力用のスレッドを作成することです。
int main(int argc, char *argv[]) { if ( argc != 3 ) { std::cout << "usage: " << argv[0] << " <input file> <output file>\n"; return 1; } std::ifstream infile(argv[1]); std::ofstream outfile(argv[2]);
入力ファイルの最初の行には材料特性が含まれており、それらを読み取ります。
float poissonRatio, youngModulus; infile >> poissonRatio >> youngModulus;
これは、平面応力状態の等方性材料の弾性マトリックスを構築するのに十分であり、次のように定義されます。

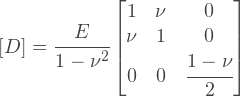
これらの表現はどこから来たのですか? それらは一般的な形でフックの法則から簡単に取得できます;実際、次の関係から行列Dの式を見つけることができます:
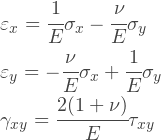
平面応力状態は、σZがゼロであることを意味しますが、 εZではないことに注意してください。 平面応力モデルは、平面構造が考慮され、すべての力が平面で作用する多くの工学的問題を解決するのに適しています。 体積の問題の計算が高すぎるとき、多くのタスクがフラットになり、精度が犠牲になりました。
平面応力状態では、身体がその平面に垂直な方向に変形するのを妨げるものはないため、歪みεZは一般にゼロに等しくありません。 上記の式には現れませんが、電圧σZがゼロの場合、次の関係から簡単に取得できます。
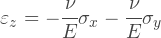
弾性行列を設定するためのすべてのソースデータがあります。これを行いましょう。
Eigen::Matrix3f D; D << 1.0f, poissonRatio, 0.0f, poissonRatio, 1.0, 0.0f, 0.0f, 0.0f, (1.0f - poissonRatio) / 2.0f; D *= youngModulus / (1.0f - pow(poissonRatio, 2.0f));
次に、ノードの座標を含むリストを読み取ります。 最初にノードの数を読み取り、次に動的ベクトルxおよびyのサイズを設定します。 次に、ループ内のノードの座標を1行ずつ読み取ります。
infile >> nodesCount; nodesX.resize(nodesCount); nodesY.resize(nodesCount); for (int i = 0; i < nodesCount; ++i) { infile >> nodesX[i] >> nodesY[i]; }
次に、アイテムのリストを読み取ります。 すべて同じです。要素の数を読み取り、次に各要素のノードインデックスを読み取ります。
int elementCount; infile >> elementCount; for (int i = 0; i < elementCount; ++i) { Element element; infile >> element.nodesIds[0] >> element.nodesIds[1] >> element.nodesIds[2]; elements.push_back(element); }
次に、ピンのリストを読みます。 すべて同じ:
int constraintCount; infile >> constraintCount; for (int i = 0; i < constraintCount; ++i) { Constraint constraint; int type; infile >> constraint.node >> type; constraint.type = static_cast<Constraint::Type>(type); constraints.push_back(constraint); }
static_castに気付くかもしれませんが、宣言したバインディングのためにint型を以前に列挙された型に変換する必要があります 。
最後に、ロードのリストを読む必要があります。 荷重に関連する特徴が1つあります。そのため、作用荷重を2倍の数のノードの次元ベクトルの形式で示します。 これを行う理由については、後ほど説明します。 次の図は、この負荷ベクトルを示しています。
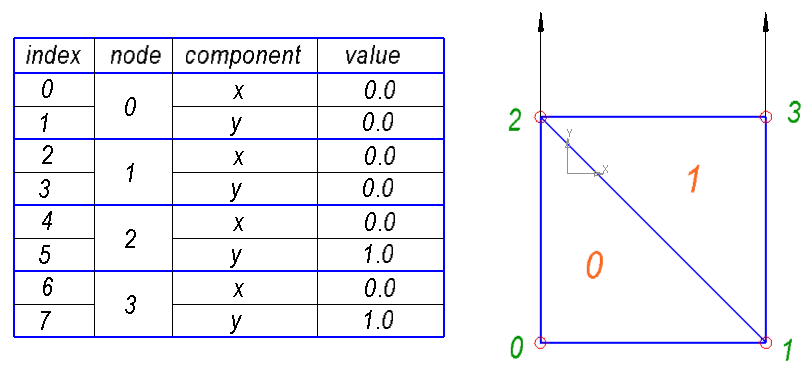
したがって、各ノードについて、荷重のxおよびy成分を表す荷重ベクトルに2つの要素があります。 したがって、特定のノードの力のxコンポーネントはインデックスid = 2 * node_id + 0の要素に格納され、このノードの力のyコンポーネントはインデックスid = 2 * node_id + 1の要素に格納されます。
まず、適用された努力のベクトルのサイズをノードの数の2倍に設定し、次にベクトルをゼロにします。 外力の数を読み取り、その値を行ごとに読み取ります。
int loadsCount; loads.resize(2 * nodesCount); loads.setZero(); infile >> loadsCount; for (int i = 0; i < loadsCount; ++i) { int node; float x, y; infile >> node >> x >> y; loads[2 * node + 0] = x; loads[2 * node + 1] = y; }
グローバル剛性マトリックスの計算
微小変位を伴う幾何学的線形システムを考えます。 さらに、変形は弾性的に発生すると仮定します。 変形は応力の線形関数です(フックの法則)。 建築構造の基礎から、各ノードの動きは、加えられた力の線形関数であることが示されます。 したがって、次の線形方程式系があると言えます。

ここで:K-剛性マトリックス; δは変位ベクトルです。 Rは荷重のベクトル、つまり外力のベクトルです。 この線形方程式系は、以下に示すように、各要素の剛性マトリックスの重ね合わせを表すため、アンサンブルと呼ばれることがよくあります。
2次元問題の変位ベクトルは、次のように定義できます。
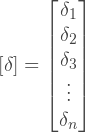
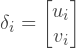
ここで、u iおよびv iは、i番目のノードの移動のuコンポーネントおよびvコンポーネントです。
外力のベクトル:
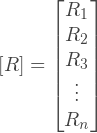
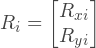
ここで、R xiとR yi -i番目のノードに適用される外力のx成分とy成分。
ご覧のとおり、変位ベクトルと負荷ベクトルの各要素は2次元ベクトルです。 代わりに、これらのベクトルを次のように定義できます。

それは実際には同じことですが、コード内のこれらのベクトルの表現を単純化します。 これは、以前にこのような特異な方法で負荷ベクトルを設定した理由の説明です。
剛性マトリックスの作成方法は? グローバル剛性マトリックスの本質は、各要素の剛性マトリックスの重ね合わせです。 1つの要素を他の要素とは別に検討すると、同じ剛性マトリックスを決定できますが、この要素についてのみです。 このマトリックスは、ノードの動きと節点力の関係を決定します。 たとえば、3ノード要素の場合:

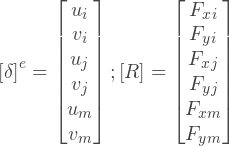
ここで、[k] eはe要素の剛性マトリックスです。 [δ] eは、e要素の節点の変位のベクトルです。 [F] eは、e要素の節点力のベクトルです。 i、j、mは、要素のノードのインデックスです。
1つのノードが2つの要素に分割されるとどうなりますか? まず第一に、これはまだ同じノードであるため、移動はこのノードを検討している要素の構成に依存しません。 2番目の重要な結果は、このノードの各要素からのすべての節点力を要約すると、結果は外力、つまり荷重に等しくなります。
各ノードのすべての節点力の合計は、このノードの外力の合計に等しくなります。これは、平衡の原理に基づいています。 この声明は非常に論理的で公平に見えるかもしれないという事実にもかかわらず、実際には、すべてが少し複雑です。 そのような定式化は正確ではありません。なぜなら、節点の力は言葉の一般的な意味での力ではなく、それらの平衡条件の実現はまったく明らかな条件ではないからです。 声明はまだ真実であるという事実にもかかわらず、それは方法の適用を制限する機械的原理を使用しています。 ポテンシャルエネルギーを最小化するという観点から、FEMにはより厳密な数学的正当化があり、この方法をより広範な問題に拡張することが可能になります。
私の意見では、ラグランジュ力学の表現において、節点力をある種の一般化された力と考える方が良いです。 実際、ノードの移動は、要素内の変位のフィールドを一意に特徴付けるため、実際には一般化された移動です。ノードの動きの各コンポーネントは、一般化された座標として解釈できます。したがって、力はノードの点ではなく、要素の境界に沿って(またはボリューム力のボリュームで)作用し、与えられたノードを特徴付ける動きに正確に作用します。
各ノードのすべての方程式を合計すると、要素間の節点力はなくなります。方程式の右側には、外力-負荷のみが残ります。したがって、この事実を考えると、次のように記述できます。

次の図は、上記の式を示しています。

グローバル剛性マトリックスを作成するには、トリプレットベクトルが必要です。ループでは、各要素を調べ、このベクトルに各要素から取得した剛性マトリックスの値を入力します。
std::vector<Eigen::Triplet<float> > triplets; for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it) { it->CalculateStiffnessMatrix(D, triplets); }
ここで、std :: vector <Eigen :: Triplet <float >> -vector triplets ; CalculateStiffnessMatrixは、トリプレットベクトルを埋める要素クラスメソッドです。
前述したように、トリプレットベクトルから直接グローバルスパース行列を構築できます。
Eigen::SparseMatrix<float> globalK(2 * nodesCount, 2 * nodesCount); globalK.setFromTriplets(triplets.begin(), triplets.end());
個々の要素の剛性マトリックスの計算
要素のマトリックスからグローバル剛性マトリックス(アンサンブル)を組み立てる方法を見つけましたが、要素の剛性マトリックスを取得する方法を見つけることは残っています。
フォーム関数
ノードの動きに基づいて要素内の動きを補間することから始めましょう。ノードの変位が指定されている場合、要素の任意の点での変位は次のように表すことができます。
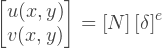
ここで、[N]は座標関数(x、y)の行列です。これらの関数はフォーム関数と呼ばれます。各変位成分uおよびvは、独立して補間することができ、上記の方程式は次の形式で書き換える
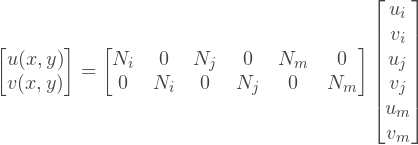
ことができます。または、別の形式で記述することができます:内


挿関数を取得するには?簡単にするために、スカラーフィールドを見てみましょう。 3ノード線形要素の場合、補間関数は線形です。次の形式で補間式を探し

ます。値がノードのfがわかっている場合、3つの方程式のシステムを指定できます:
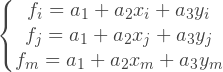
または行列形式:

この方程式のシステムから、補間式の未知の係数ベクトルを見つけることができます:
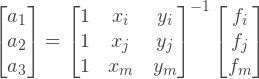
表記法を導入します
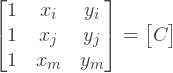
最後に、補間式を取得します:
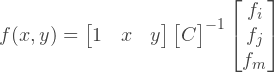
変位に戻る、と言うことができますwhat:

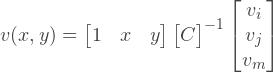
次に、フォーム関数は次のようになります。

変形と勾配行列
変位場を知ると、弾性の理論からの関係に従って、変形場を見つけることができます:
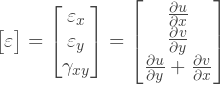
ここで、uとvを次の形式の関数に置き換える
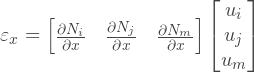

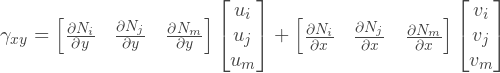
ことができます:または、同じ形式を組み合わせた形式で書くことができます:

通常、行列Bとして示される右側の行列、いわゆる勾配行列。

行列Bを見つけるには、フォーム関数のすべての偏導関数を見つける必要があります:


線形要素の場合、フォーム関数の偏導関数は実際には定数であり、以下に示すように、多くの労力を節約できます。行ベクトルに定数を乗算すると、逆行列Cが得られます。


これで、B行列を計算できます。行列Cを作成するには、まずノードの座標ベクトルを定義します。
Eigen::Vector3f x, y; x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]]; y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]];
次に、3行から行列Cを作成できます。
Eigen::Matrix3f C; C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y;
次に、逆行列Cを計算し、行列Bを収集します。
Eigen::Matrix3f IC = C.inverse(); for (int i = 0; i < 3; i++) { B(0, 2 * i + 0) = IC(1, i); B(0, 2 * i + 1) = 0.0f; B(1, 2 * i + 0) = 0.0f; B(1, 2 * i + 1) = IC(2, i); B(2, 2 * i + 0) = IC(2, i); B(2, 2 * i + 1) = IC(1, i); }
ストレスへの移行
前述のように、応力とひずみの関係は弾性行列Dを使用して記述できます。

したがって、上記の式をひずみの関係に代入すると、次のようになり

ます。ここで、応力はひずみと同様に要素内の定数であることがわかります。これは線形要素の特徴です。ただし、高次の要素の場合、応力の連続性も満たされません。要素の数が増えると、これらのギャップが減少するはずです。これが収束の基準です。実際には、各ノードの平均ひずみ値が通常計算されますが、この例では、すべてをそのままにします。
バーチャルワークの原理
剛性マトリックスに移動するには、仮想作業に切り替える必要があります。要素のノードにいくつかの仮想変位があるとしましょう:d [δ] e
仮想変位は、発生する可能性のある無限に小さな変位として理解されるべきです。私たちのタスクの場合、解決策は1つだけで、動きのセットは1つしか発生しないことがわかっていますが、ここではすべてをわずかに異なる角度から見ます。言い換えると、運動学的に許容されるすべての微小変位を取得し、物理法則を満たす唯一の変位を見つけます。
これらの仮想運動の場合、節点力の仮想作業は次のようになります。

同じ仮想運動の単位体積あたりの内部応力の仮想作業:

または:
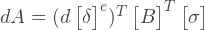
, :

, :
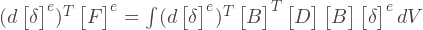
, , :

, . , , , :
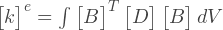
, , . , :

ここで、Aは要素の面積、tは要素の厚さです。三角形のプロパティから、その面積は行列Cの行列式の半分として取得できます。

最後に、剛性行列を計算する次のコードを記述できます。
Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f;
ここで厚さを減らしましたが、私たちはそれが私たちと一緒であると仮定します。通常、実際には、次の単位システムを使用します:MPa、mm 2。この場合、弾性率をメガパスカルで、寸法をミリメートルで設定すると、厚さは1ミリメートルになります。異なる厚さが必要な場合、弾性係数に簡単に導入できます。より一般的なケースでは、厚さを要素ごとに設定するか、各ノードに設定することをお勧めします。CalculateStiffnessMatrix
メソッド全体:
void Element::CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets) { Eigen::Vector3f x, y; x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]]; y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]]; Eigen::Matrix3f C; C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y; Eigen::Matrix3f IC = C.inverse(); for (int i = 0; i < 3; i++) { B(0, 2 * i + 0) = IC(1, i); B(0, 2 * i + 1) = 0.0f; B(1, 2 * i + 0) = 0.0f; B(1, 2 * i + 1) = IC(2, i); B(2, 2 * i + 0) = IC(2, i); B(2, 2 * i + 1) = IC(1, i); } Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { Eigen::Triplet<float> trplt11(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 0, K(2 * i + 0, 2 * j + 0)); Eigen::Triplet<float> trplt12(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 1, K(2 * i + 0, 2 * j + 1)); Eigen::Triplet<float> trplt21(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 0, K(2 * i + 1, 2 * j + 0)); Eigen::Triplet<float> trplt22(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 1, K(2 * i + 1, 2 * j + 1)); triplets.push_back(trplt11); triplets.push_back(trplt12); triplets.push_back(trplt21); triplets.push_back(trplt22); } } }
メソッドの最後に、剛性マトリックスを計算した後、トリプレットベクトルが塗りつぶされます。各トリプレットは、要素ノードインデックスの配列を使用して作成され、グローバル剛性マトリックス内の位置を決定します。念のため、2つのインデックスのセットがあることを強調します。1つは要素行列に対してローカルで、もう1つはアンサンブルに対してグローバルです。
ジョブに参加する
結果の線形方程式系は、修正するまで解けません。純粋に機械的な観点から見ると、固定されていないシステムは大きな変位を行うことができ、外力の影響下で完全に動き始めます。数学的には、これにより、取得したSLAEが線形独立ではないため、独自の解決策がないという事実につながります。
一部のノードの動きは、ゼロまたは所定の値に設定する必要があります。最も単純なケースでは、初期オフセットなしで、ノードの修正のみを検討しましょう。実際、これはシステムからいくつかの方程式を削除していることを意味します。しかし、システム方程式の量をその場で変更することは簡単な作業ではありません。代わりに、次のトリックを使用できます。
次の方程式系が
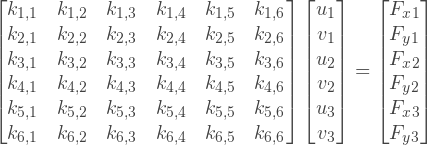
あるとします。ノードを修正するには、対応する行列要素を1に設定し、この要素を含む行と列のすべての要素をゼロに設定する必要があります。また、制限が作用する方向に固定ユニットに作用する外力があってはなりません。このノードを含む方程式は、このノードのゼロオフセットを明示的に与え、対応する列のゼロはこのオフセットを他の方程式から除外します。 x軸方向にゼロノードを修正し、y軸方向に最初のノードを修正するとします。

この操作を実行するには、まずSLAEから除外する方程式のインデックスを決定します。これを行うには、サイクル内のピンのリストを調べて、インデックスベクトルを収集します。次に、剛性マトリックスのすべての非ゼロ要素をソートして、SetConstraints関数を呼び出します。以下は、ApplyConstraints関数です。
void ApplyConstraints(Eigen::SparseMatrix<float>& K, const std::vector<Constraint>& constraints) { std::vector<int> indicesToConstraint; for (std::vector<Constraint>::const_iterator it = constraints.begin(); it != constraints.end(); ++it) { if (it->type & Constraint::UX) { indicesToConstraint.push_back(2 * it->node + 0); } if (it->type & Constraint::UY) { indicesToConstraint.push_back(2 * it->node + 1); } } for (int k = 0; k < K.outerSize(); ++k) { for (Eigen::SparseMatrix<float>::InnerIterator it(K, k); it; ++it) { for (std::vector<int>::iterator idit = indicesToConstraint.begin(); idit != indicesToConstraint.end(); ++idit) { SetConstraints(it, *idit); } } } }
SetConstraints関数は、剛性マトリックス要素が除外された方程式の一部であるかどうかを確認し、その場合、要素が対角線上にあるかどうかに応じて、ゼロまたは1に設定します。
void SetConstraints(Eigen::SparseMatrix<float>::InnerIterator& it, int index) { if (it.row() == index || it.col() == index) { it.valueRef() = it.row() == it.col() ? 1.0f : 0.0f; } }
次に、単にApplyConstraintsを呼び出して、グローバル剛性マトリックスと補強ベクトルを引数として渡します。
ApplyConstraints(globalK, constraints);
SLAUソリューションと出力
Eigenライブラリには、さまざまなスパース線形方程式ソルバーが用意されています。高速の直接ソルバーであるSimplicialLDLTを使用します。デモンストレーションのために、元の剛性マトリックスと荷重ベクトルを導出し、解の結果である変位ベクトルを出力します。
std::cout << "Global stiffness matrix:\n"; std::cout << static_cast<const Eigen::SparseMatrixBase<Eigen::SparseMatrix<float> >& > (globalK) << std::endl; std::cout << "Loads vector:" << std::endl << loads << std::endl << std::endl; Eigen::SimplicialLDLT<Eigen::SparseMatrix<float> > solver(globalK); Eigen::VectorXf displacements = solver.solve(loads); std::cout << "Displacements vector:" << std::endl << displacements << std::endl; outfile << displacements << std::endl;
もちろん、マトリックス推論は、2つの要素のみを含むテストケースでのみ意味があります。
結果の分析
前に見たように、変位からひずみ、そして応力へと移動できます:

ただし、一般的に言えば弾性理論では第2ランクの対称テンソルである応力ベクトルを取得し
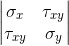
ます:ご存知のように、テンソル要素は座標系に直接依存しますが、もちろん、物理的な状態自体は独立しています。したがって、分析のために、ある種の不変量として検討する方が適切であり、スカラーにするのが最善です。ミーゼス応力はそのような不変量です。
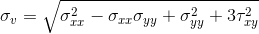
このスカラー量により、一軸応力状態を扱っているかのように、複雑な応力状態の応力を推定できます。この基準は理想的ではありませんが、ほとんどの場合、静的分析では多かれ少なかれ妥当な画像を提供するため、実際に最もよく使用されます。
次に、サイクル内のすべての要素を調べて、各要素のミーゼス応力を計算します。
std::cout << "Stresses:" << std::endl; for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it) { Eigen::Matrix<float, 6, 1> delta; delta << displacements.segment<2>(2 * it->nodesIds[0]), displacements.segment<2>(2 * it->nodesIds[1]), displacements.segment<2>(2 * it->nodesIds[2]); Eigen::Vector3f sigma = D * it->B * delta; float sigma_mises = sqrt(sigma[0] * sigma[0] - sigma[0] * sigma[1] + sigma[1] * sigma[1] + 3.0f * sigma[2] * sigma[2]); std::cout << sigma_mises << std::endl; outfile << sigma_mises << std::endl; }
これについては、最も単純なFEM計算機の記述は完了していると考えることができます。テスト問題に対してどのような結論が得られるか見てみましょう。
Global stiffness matrix: 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1483.52 0 0 714.286 -384.615 -384.615 0 0 0 1 0 0 0 0 0 0 0 0 1483.52 0 -1098.9 -329.67 0 0 714.286 0 0 1483.52 -384.615 -384.615 0 0 -384.615 0 -1098.9 -384.615 1483.52 714.286 0 0 -384.615 0 -329.67 -384.615 714.286 1483.52 Loads vector: 0 0 0 0 0 1 0 1 Deformations vector: 0 0 -0.0003 0 -5.27106e-011 0.001 -0.0003 0.001 Stresses: 2 2
固定を正しく設定すると、対応する方向の固定ノードの変形はゼロになります。上部ノードの変形は、張力に応じて上方に向けられます。ノードの右側のペアのx方向の変形は0.0003で、これはy方向の上部ノードの変形の0.3部分であり、これはポアソン効果です。計算結果は期待と完全に一致しているため、より興味深いタスクに進むことができます。
全コード
#include <Eigen/Dense> #include <Eigen/Sparse> #include <string> #include <vector> #include <iostream> #include <fstream> struct Element { void CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets); Eigen::Matrix<float, 3, 6> B; int nodesIds[3]; }; struct Constraint { enum Type { UX = 1 << 0, UY = 1 << 1, UXY = UX | UY }; int node; Type type; }; int nodesCount; Eigen::VectorXf nodesX; Eigen::VectorXf nodesY; Eigen::VectorXf loads; std::vector< Element > elements; std::vector< Constraint > constraints; void Element::CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets) { Eigen::Vector3f x, y; x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]]; y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]]; Eigen::Matrix3f C; C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y; Eigen::Matrix3f IC = C.inverse(); for (int i = 0; i < 3; i++) { B(0, 2 * i + 0) = IC(1, i); B(0, 2 * i + 1) = 0.0f; B(1, 2 * i + 0) = 0.0f; B(1, 2 * i + 1) = IC(2, i); B(2, 2 * i + 0) = IC(2, i); B(2, 2 * i + 1) = IC(1, i); } Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { Eigen::Triplet<float> trplt11(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 0, K(2 * i + 0, 2 * j + 0)); Eigen::Triplet<float> trplt12(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 1, K(2 * i + 0, 2 * j + 1)); Eigen::Triplet<float> trplt21(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 0, K(2 * i + 1, 2 * j + 0)); Eigen::Triplet<float> trplt22(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 1, K(2 * i + 1, 2 * j + 1)); triplets.push_back(trplt11); triplets.push_back(trplt12); triplets.push_back(trplt21); triplets.push_back(trplt22); } } } void SetConstraints(Eigen::SparseMatrix<float>::InnerIterator& it, int index) { if (it.row() == index || it.col() == index) { it.valueRef() = it.row() == it.col() ? 1.0f : 0.0f; } } void ApplyConstraints(Eigen::SparseMatrix<float>& K, const std::vector<Constraint>& constraints) { std::vector<int> indicesToConstraint; for (std::vector<Constraint>::const_iterator it = constraints.begin(); it != constraints.end(); ++it) { if (it->type & Constraint::UX) { indicesToConstraint.push_back(2 * it->node + 0); } if (it->type & Constraint::UY) { indicesToConstraint.push_back(2 * it->node + 1); } } for (int k = 0; k < K.outerSize(); ++k) { for (Eigen::SparseMatrix<float>::InnerIterator it(K, k); it; ++it) { for (std::vector<int>::iterator idit = indicesToConstraint.begin(); idit != indicesToConstraint.end(); ++idit) { SetConstraints(it, *idit); } } } } int main(int argc, char *argv[]) { if ( argc != 3 ) { std::cout<<"usage: "<< argv[0] <<" <input file> <output file>\n"; return 1; } std::ifstream infile(argv[1]); std::ofstream outfile(argv[2]); float poissonRatio, youngModulus; infile >> poissonRatio >> youngModulus; Eigen::Matrix3f D; D << 1.0f, poissonRatio, 0.0f, poissonRatio, 1.0, 0.0f, 0.0f, 0.0f, (1.0f - poissonRatio) / 2.0f; D *= youngModulus / (1.0f - pow(poissonRatio, 2.0f)); infile >> nodesCount; nodesX.resize(nodesCount); nodesY.resize(nodesCount); for (int i = 0; i < nodesCount; ++i) { infile >> nodesX[i] >> nodesY[i]; } int elementCount; infile >> elementCount; for (int i = 0; i < elementCount; ++i) { Element element; infile >> element.nodesIds[0] >> element.nodesIds[1] >> element.nodesIds[2]; elements.push_back(element); } int constraintCount; infile >> constraintCount; for (int i = 0; i < constraintCount; ++i) { Constraint constraint; int type; infile >> constraint.node >> type; constraint.type = static_cast<Constraint::Type>(type); constraints.push_back(constraint); } loads.resize(2 * nodesCount); loads.setZero(); infile >> loadsCount; int loadsCount; for (int i = 0; i < loadsCount; ++i) { int node; float x, y; infile >> node >> x >> y; loads[2 * node + 0] = x; loads[2 * node + 1] = y; } std::vector<Eigen::Triplet<float> > triplets; for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it) { it->CalculateStiffnessMatrix(D, triplets); } Eigen::SparseMatrix<float> globalK(2 * nodesCount, 2 * nodesCount); globalK.setFromTriplets(triplets.begin(), triplets.end()); ApplyConstraints(globalK, constraints); Eigen::SimplicialLDLT<Eigen::SparseMatrix<float> > solver(globalK); Eigen::VectorXf displacements = solver.solve(loads); outfile << displacements << std::endl; for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it) { Eigen::Matrix<float, 6, 1> delta; delta << displacements.segment<2>(2 * it->nodesIds[0]), displacements.segment<2>(2 * it->nodesIds[1]), displacements.segment<2>(2 * it->nodesIds[2]); Eigen::Vector3f sigma = D * it->B * delta; float sigma_mises = sqrt(sigma[0] * sigma[0] - sigma[0] * sigma[1] + sigma[1] * sigma[1] + 3.0f * sigma[2] * sigma[2]); outfile << sigma_mises << std::endl; } return 0; }
clocユーティリティを実行します。
------------------------------------------------------------------------------- Language files blank comment code ------------------------------------------------------------------------------- C++ 1 37 0 171 -------------------------------------------------------------------------------
ご覧のとおり、何もありません-171行のコード。
いくつかの写真
計算結果を視覚化するために、応力場を持つ非変形および変形メッシュを描くPython スクリプトが作成されました。残念ながら、PILを使用してグラデーション塗りつぶしを行う方法がわかりません。そのため、要素内の応力は、一定の塗りつぶしとして表示されます。Abaqusは、見た目はあまり美しくないものの、より真実に近い方法で視覚化を行うことができます。
テストタスク:

より複雑なグリッドを取得するために、Abaqusの無料の学生版が使用されました。Abaqusの入力ファイルを変換するために、別のスクリプトが作成されました。確かに、固定荷重と外部荷重は手動で設定する必要があります。
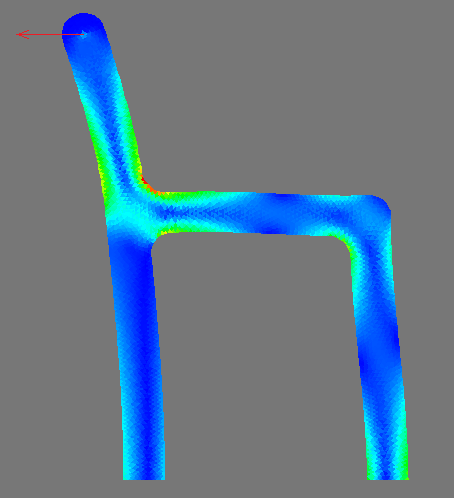
ここでは、穴があり、その底部が固定され、上端に張力が加えられているストリップがあり

ます。美しさのためだけの抽象的な設計要素です。構造の底部は固定されており、写真の上部にすでに描いた上部の突出部に集中力が加えられています:
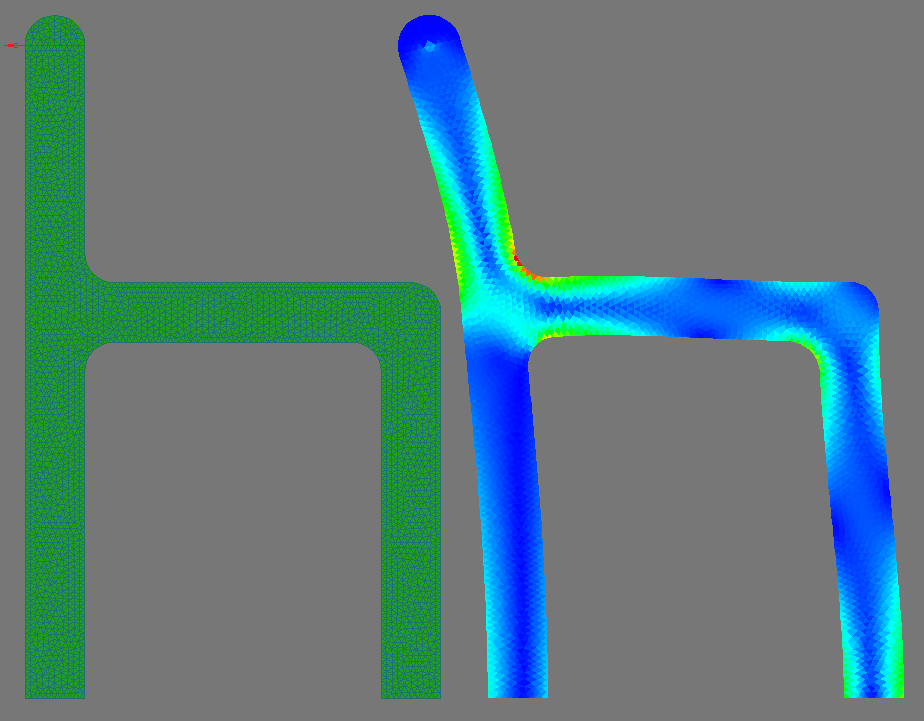
穴のあるストリップの別の例では、対称性のために構造の4分の1だけが考慮されます。左の境界線はx軸に沿って固定され、下部はy軸に沿って固定されます。最大受信電圧:3.05152この値は、グリッドの粗さにも関わらず(おそらくそれによる)、理論値-3に非常に近いです。
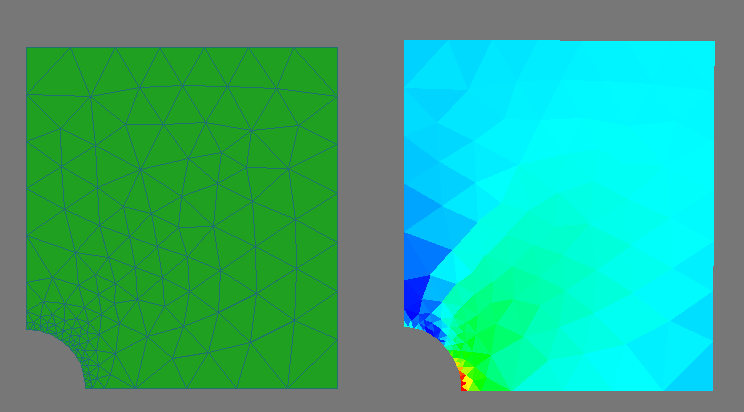
同じ問題がAbaqusで解決されました。ご覧のとおり、最大電圧は3.052であり、これは結果と完全に一致しています。実際には、三角形要素が独自の方法で何かを行うことは困難であるため、結果が異なるため、このような正確な一致は原則として驚くべきことではありません。残念ながら、高次の要素については、この100%の一致はうまくいきませんでした。これは、数値積分の異なる実装によって説明できます。
例を含むすべてのソースコードはgithubで入手できます。
舞台裏に残っているもの
正直なところ、多くのことが舞台裏に残されています。しかし、記事はすでに膨らんでいたので、そこでやめることができると思います。
含まれていません(ただし、必要でした):
- . , . . , ( 2- 4- ), . , ( ).
- .
- , .
- - , . , .
- , , .
- 節点力の平衡を考慮することにより、一般的にこれらの節点力を除外して、より一般的な方法を正当化することができました。
MATLABなどの最新の数学パッケージにはFEMを操作するためのツールがあり、原則としてC ++で何かを記述する必要がないことに多くの人が正しく気付くと思います。ただし、ここでは、依存関係を最小限に抑えた最小限の実装、つまり、サードパーティのツールを使用せずに。もちろん、数学ライブラリを除いて、読者に使用されるすべての機能は非常に透明である必要があると思います。
PS記事は大きいので、PMにタイプミスが多いと思います。