Pythonの11行のニューラルネットワーク

についての記事は何ですか

個人的には、遊ぶことができる小さな作業コードで最もよく学びます。 このチュートリアルでは、Pythonで実装された小さなニューラルネットワークの例を使用して、逆伝播アルゴリズムを学習します。

コードを与えてください！

X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T syn0 = 2*np.random.random((3,4)) - 1 syn1 = 2*np.random.random((4,1)) - 1 for j in xrange(60000): l1 = 1/(1+np.exp(-(np.dot(X,syn0)))) l2 = 1/(1+np.exp(-(np.dot(l1,syn1)))) l2_delta = (y - l2)*(l2*(1-l2)) l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1)) syn1 += l1.T.dot(l2_delta) syn0 += XTdot(l1_delta)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

簡潔すぎますか？ それをより単純な部分に分けましょう。

パート1：小さなおもちゃのニューラルネットワーク

バックプロパゲーションを通じて訓練されたニューラルネットワークは、入力を使用して出力を予測しようとします。

   0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

入力に基づいて出力列がどのようになるかを予測する必要があるとします。 この問題は、それらの間の統計的対応を計算することで解決できます。 そして、左の列が出力と100％相関していることがわかります。



逆伝播は、最も単純な場合、同様の統計を計算してモデルを作成します。 やってみましょう。

2層のニューラルネットワーク

 import numpy as np #  def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1-f(x)) return 1/(1+np.exp(-x)) #    X = np.array([ [0,0,1], [0,1,1], [1,0,1], [1,1,1] ]) #   y = np.array([[0,0,1,1]]).T #      np.random.seed(1) #       0 syn0 = 2*np.random.random((3,1)) - 1 for iter in xrange(10000): #   l0 = X l1 = nonlin(np.dot(l0,syn0)) #   ? l1_error = y - l1 #      #     l1 l1_delta = l1_error * nonlin(l1,True) # !!! #   syn0 += np.dot(l0.T,l1_delta) # !!! print "   :" print l1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

    : [[ 0.00966449] [ 0.00786506] [ 0.99358898] [ 0.99211957]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

変数とその説明。



Xは入力データセットの行列です。 文字列-トレーニングの例

yは、出力データセットの行列です。 文字列-トレーニングの例

l0-入力データによって定義されたネットワークの最初の層

l1-ネットワークの2番目の層、または非表示層

syn0-重みの最初のレイヤーSynapse 0は、l0とl1を組み合わせます。

"*"-要素単位の乗算-同じサイズの2つのベクトルが対応する値を乗算し、出力は同じサイズのベクトルになります

"-"-ベクトルの要素ごとの減算

x.dot（y）-xとyがベクトルの場合、出力はスカラー積になります。 これらが行列の場合、行列の乗算が取得されます。 行列がそれらの1つだけの場合、これはベクトルと行列の乗算です。



そしてそれは動作します！ 説明を読む前に、コードを少し遊んでみて、その仕組みを理解することをお勧めします。 ipythonノートブックの場合と同じように起動するはずです。 コードで修正できるもの：

• 最初の反復後と最後の反復後のl1を比較する
• nonlin関数を見てください。
• l1_errorの変化を見る
• 36行目を分解-主な秘密の成分がここに集められます（マーク付き!!!）
• 39行目を逆アセンブルします-ネットワーク全体がこの操作の準備をしています（マーク!!!）

コードを行に解析してみましょう

 import numpy as np
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

線形代数ライブラリnumpyをインポートします。 私たちの唯一の中毒。

 def nonlin(x,deriv=False):
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

非線形性。 具体的には、この関数は「シグモイド」を作成します。 任意の数値を0〜1の値に関連付け、数値を確率に変換します。また、ニューラルネットワークのトレーニングに役立つその他のプロパティもいくつかあります。

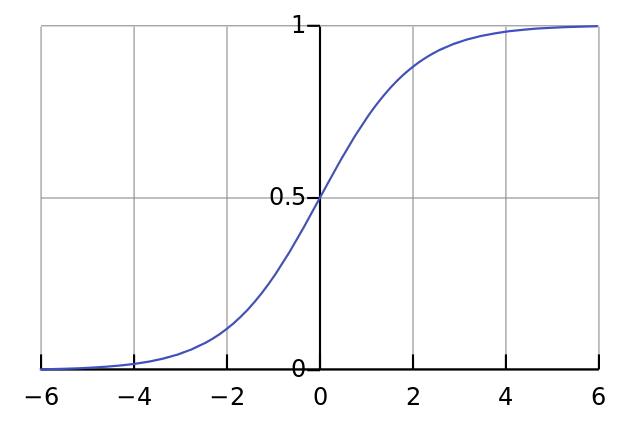
 if(deriv==True):
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数は、シグモイドの微分を生成することもできます（deriv = True）。 これは便利なプロパティの1つです。 関数の出力がout変数の場合、導関数はout *（1-out）になります。 事実上。

 X = np.array([ [0,0,1], …
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

numpy行列の形式での入力データ配列の初期化。 各行はトレーニングの例です。 列は入力ノードです。 ネットワーク内に3つの入力ノードと4つのトレーニング例があります。

 y = np.array([[0,0,1,1]]).T
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

出力を初期化します。 「.T」は伝達関数です。 転送後、行列yには4つの行と1つの列があります。 入力データの場合と同様に、各行はトレーニングの例であり、各列（この例では1つ）は出力ノードです。 ネットワークには、3つの入力と1つの出力があります。

 np.random.seed(1)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより、ランダム分布は毎回同じになります。 これにより、コードを変更した後、ネットワークをより簡単に監視できるようになります。

 syn0 = 2*np.random.random((3,1)) – 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

マトリックスネットワークの重み。 syn0はシナプスゼロを意味します。 入力と出力の2つのレイヤーしかないため、それらを接続する重みのマトリックスが1つ必要です。 3つの入力と1つの出力があるため、その次元は（3、1）です。 つまり、l0のサイズは3で、l1は1です。l0のすべてのノードをすべてのノードl1に接続するため、次元（3、1）の行列が必要です。



ランダムに初期化され、平均値はゼロであることに注意してください。 この背後にはかなり複雑な理論があります。 とりあえず、単に推奨事項として使用してください。 また、ニューラルネットワークにも注意してください。これがまさにこのマトリックスです。 「レイヤー」l0とl1がありますが、これらはデータセットに基づく一時的な値です。 それらは保存しません。 すべてのトレーニングはsyn0に保存されます。

 for iter in xrange(10000):
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これが、メインのネットワークトレーニングコードの始まりです。 コードのサイクルは何度も繰り返され、データセットのネットワークを最適化します。

 l0 = X
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初のレイヤーl0は単なるデータです。 Xには4つのトレーニング例が含まれています。 一度にすべて処理します-これはグループトレーニング[フルバッチ]と呼ばれます。 合計で4つの異なる行l0がありますが、それらを1つのトレーニング例と考えることができます-この段階では問題になりません（コードを変更せずに1000または10000をロードできます）。

 l1 = nonlin(np.dot(l0,syn0))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは予測ステップです。 ネットワークに入力に基づいて出力を予測させます。 その後、彼女が改善の方向に修正できるように、彼女がそれをどのように行うかを見ていきます。



行には2つのステップが含まれます。 最初は、l0とsyn0の行列乗算を行います。 2番目は出力をシグモイドに渡します。 それらの寸法は次のとおりです。

 (4 x 3) dot (3 x 1) = (4 x 1)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

行列の乗算では、中間で次元方程式が一致する必要があります。 結果のマトリックスには、最初のような行数と、2番目のような列数があります。



4つのトレーニングサンプルをダウンロードし、4つの推測（4x1マトリックス）を得ました。 各ピンは、特定の入力に対するネットワーク推測に対応しています。

 l1_error = y - l1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

l1には推測が含まれているため、正解yからl1を減算することで、それらの違いを現実と比較できます。 l1_error-ネットワークの「ミス」を特徴付ける正と負の数のベクトル。

  l1_delta = l1_error * nonlin(l1,True)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、ここに秘密の成分があります。 この行は、部品ごとに分解する必要があります。



最初の部分：微分

 nonlin(l1,True)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

l1はこれら3つのポイントを表し、コードは以下に示す線の勾配を生成します。 x = 2.0（緑の点）のような大きな値とx = -1.0（紫）のような非常に小さな値では、線にわずかな勾配があることに注意してください。 ポイントx = 0（青）での最大角度。 これは非常に重要です。 また、すべての導関数は0から1の間であることに注意してください。







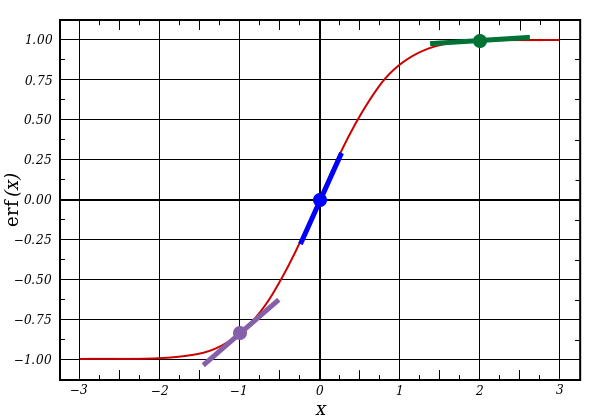
完全な式：エラー加重微分

 l1_delta = l1_error * nonlin(l1,True)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

数学的には、より正確な方法がありますが、私たちの場合、これも適しています。 l1_errorは行列（4,1）です。 nonlin（l1、True）は、行列（4,1）を返します。 ここで、それらを要素ごとに乗算し、出力で行列（4.1）l1_deltaも取得します。



導関数にエラーを掛けることで、高い信頼性で行われた予測のエラーを減らします。 線の勾配が小さかった場合、ネットワークには非常に大きな値または非常に小さな値が含まれます。 ネットワーク上の推測がゼロに近い場合（x = 0、y = 0.5）、それは特に確実ではありません。 これらの不確実な予測を更新し、予測に高い信頼性を与え、ゼロに近い値を掛けます。

 syn0 += np.dot(l0.T,l1_delta)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ネットワークをアップグレードする準備ができました。 1つのトレーニング例を検討してください。 その中で、重みを更新します。 左端の重みを更新します（9.5）

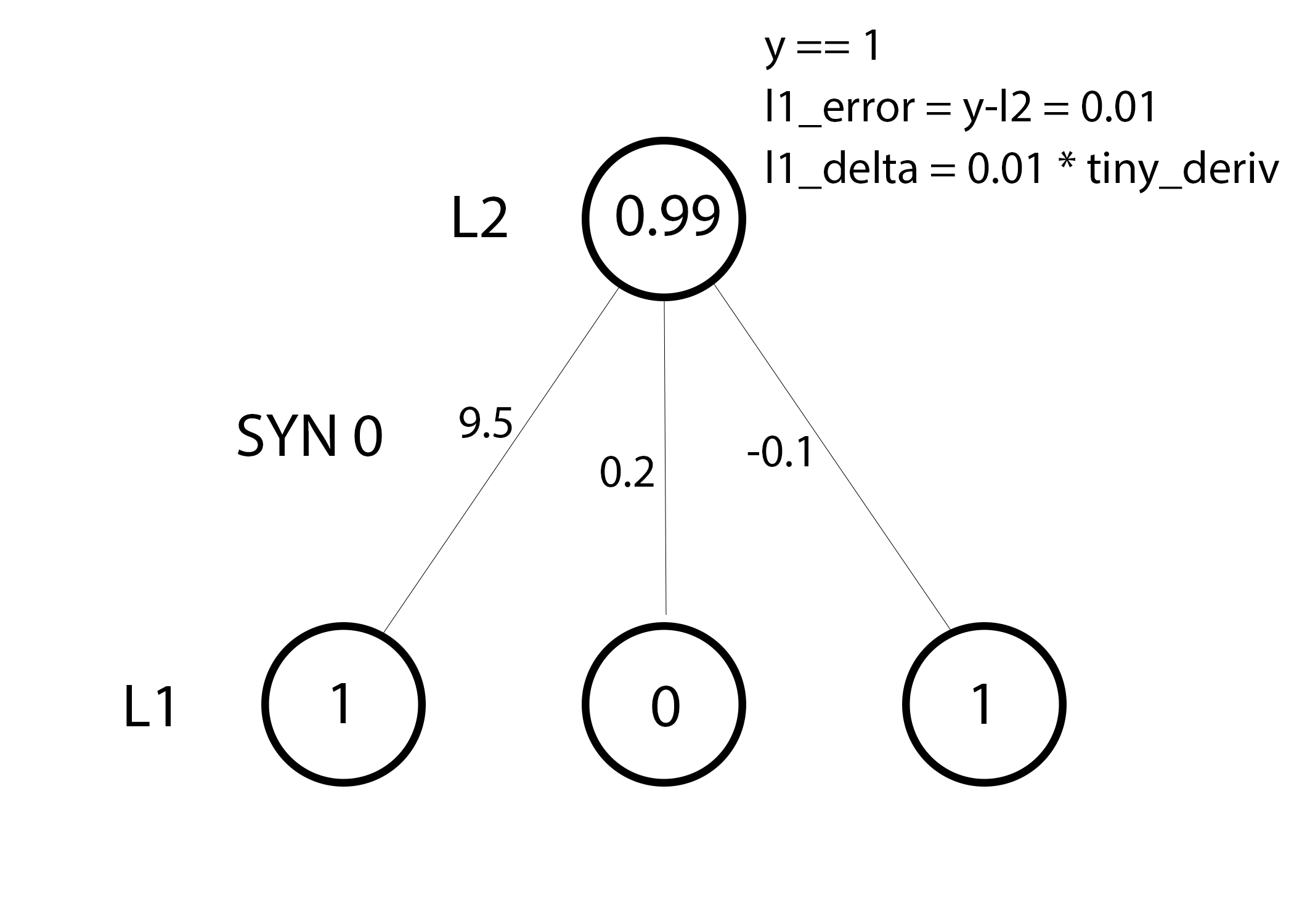
 weight_update = input_value * l1_delta
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

左端の重みの場合、これは1.0 * l1_deltaになります。 おそらく、これはわずかに9.5しか増加しません。 なんで？ 予測はすでにかなり自信があり、予測はほぼ正しかったためです。 わずかな誤差とわずかな線の傾きは、非常に小さな更新を意味します。







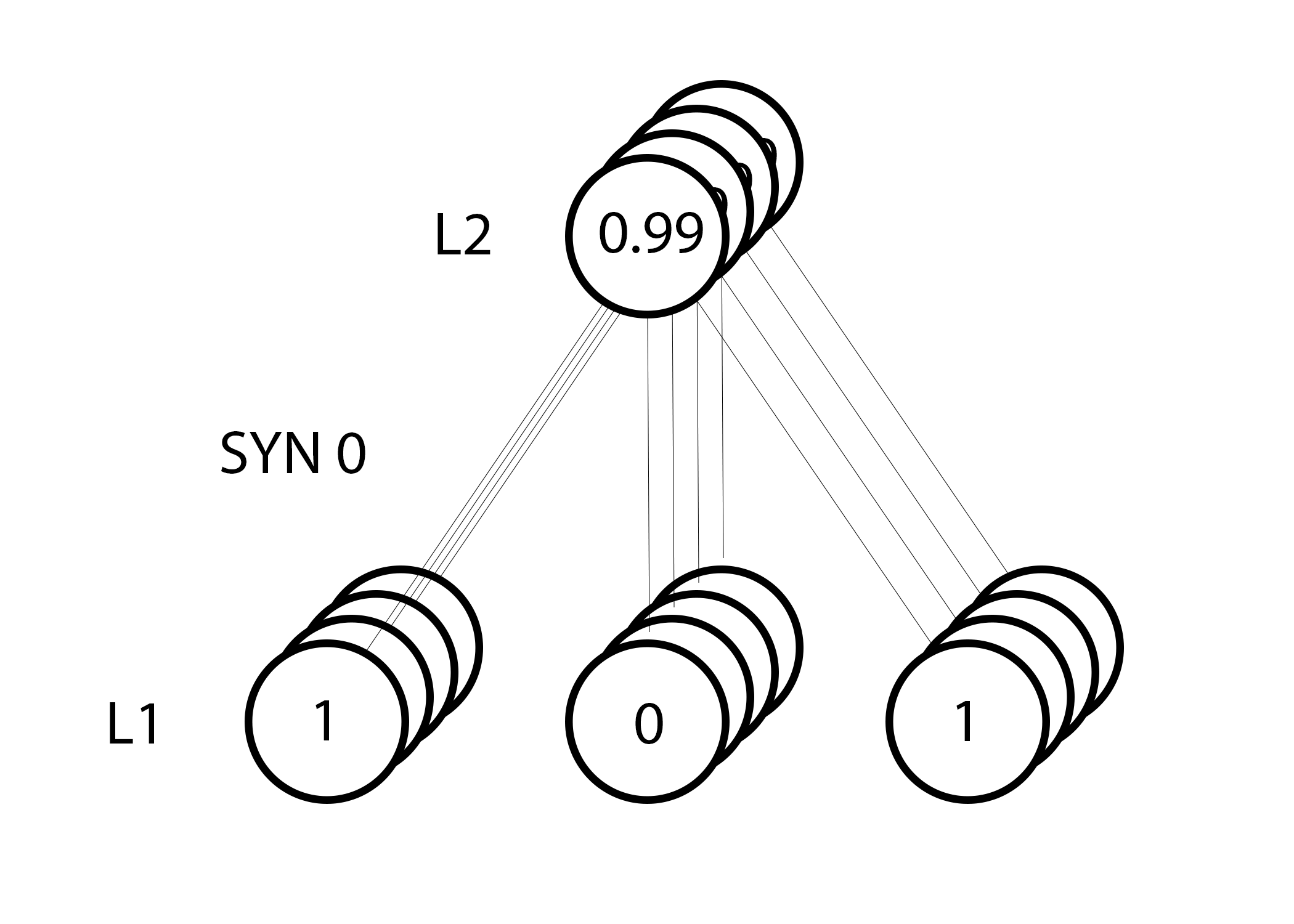
ただし、グループトレーニングを行っているため、4つのトレーニングの例すべてについて上記の手順を繰り返します。 したがって、上の画像と非常によく似ています。 それで、私たちのラインは何をしますか？ 彼女は、各トレーニングの例ごとにウェイトの更新をカウントし、それらを要約して、すべてのウェイトを更新します。



ネットワークの更新を確認した後、トレーニングデータに戻ります。 入力と出力の両方が1の場合、それらの間の重みを増やします。 入力が1で出力が0の場合、重みを減らします。

   0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、以下の4つのトレーニングの例では、出力に対する最初のエントリの重みは常に増加または一定になり、他の2つの重みは例に応じて増加および減少します。 この効果は、入力データと出力データの相関に基づいたネットワークの学習にも貢献します。

パート2：タスクはより困難です

   0 0 1 0 0 1 1 1 1 0 1 1 1 1 1 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

3つの入力データ列に基づいて出力を予測してみましょう。 どの入力列も出力と100％の相関関係はありません。 3番目の列は、ユニットがすべて含まれているため、何にも接続されていません。 ただし、ここでは図を見ることができます-最初の2列のいずれか（同時に両方ではない）に1が含まれている場合、結果も1になります。



これは、列間に1対1の直接的な対応がないため、非線形スキームです。 対応は、入力データ、列1および2の組み合わせに基づいて構築されます。



興味深いことに、パターン認識は非常によく似たタスクです。 自転車と喫煙パイプを表す同じサイズの画像が100個ある場合、それらの特定の場所にある特定のピクセルの存在は、画像内の自転車またはパイプの存在と直接相関しません。 統計的に、それらの色はランダムに見えるかもしれません。 しかし、ピクセルのいくつかの組み合わせはランダムではありません-自転車（またはチューブ）の画像を形成するもの。

戦略

ピクセルを出力と1対1で対応できるものに結合するには、別のレイヤーを追加する必要があります。 最初のレイヤーは入力を結合し、2番目は最初のレイヤーの出力を入力として使用して、出力に一致を割り当てます。 テーブルに注意してください。

  (l0)   (l1)  (l2) 0 0 1 0.1 0.2 0.5 0.2 0 0 1 1 0.2 0.6 0.7 0.1 1 1 0 1 0.3 0.2 0.3 0.9 1 1 1 1 0.2 0.1 0.3 0.8 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ランダムに重みを割り当てることにより、レイヤー1の隠された値を取得します。 興味深いことに、非表示の重みの2番目の列には、出力とすでにわずかな相関関係があります。 完璧ではありませんが、あります。 また、これはネットワークトレーニングプロセスの重要な部分でもあります。 トレーニングはこの相関関係を強化するだけです。 syn1を更新して対応を出力に割り当て、syn0を更新して入力からデータを受信しやすくします。

3層ニューラルネットワーク

 import numpy as np def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1-f(x)) return 1/(1+np.exp(-x)) X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]]) y = np.array([[0], [1], [1], [0]]) np.random.seed(1) #   ,   - 0 syn0 = 2*np.random.random((3,4)) - 1 syn1 = 2*np.random.random((4,1)) - 1 for j in xrange(60000): #     0, 1  2 l0 = X l1 = nonlin(np.dot(l0,syn0)) l2 = nonlin(np.dot(l1,syn1)) #       ? l2_error = y - l2 if (j% 10000) == 0: print "Error:" + str(np.mean(np.abs(l2_error))) #     ? #      ,       l2_delta = l2_error*nonlin(l2,deriv=True) #    l1     l2? l1_error = l2_delta.dot(syn1.T) #     ,    l1? #      ,       l1_delta = l1_error * nonlin(l1,deriv=True) syn1 += l1.T.dot(l2_delta) syn0 += l0.T.dot(l1_delta)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 Error:0.496410031903 Error:0.00858452565325 Error:0.00578945986251 Error:0.00462917677677 Error:0.00395876528027 Error:0.00351012256786
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

変数とその説明

Xは入力データセットの行列です。 文字列-トレーニングの例

yは、出力データセットの行列です。 文字列-トレーニングの例

l0-入力データによって定義されたネットワークの最初の層

l1-ネットワークの2番目の層、または非表示層

l2は最終層であり、これが私たちの仮説です。 運動するにつれて、正しい答えに近づく必要があります。

syn0-重みの最初のレイヤーSynapse 0は、l0とl1を組み合わせます。

syn1-重みの2番目のレイヤーSynapse 1は、l1とl2を組み合わせます。

l2_error-定量的に見たネットワークミス

l2_delta-予測の信頼度に応じたネットワークエラー。 信頼できる予測を除き、エラーとほぼ一致

l1_error-l2_deltaをsyn1の重みで重み付けすることにより、中間層/隠れ層の誤差を計算します

l1_delta-l1からのネットワークエラー。予測可能性に従ってスケーラブルです。 自信のある予測を除いて、l1_errorとほぼ同じ



コードは十分に明確である必要があります-それは、ネットワークの2つの層に上下に折り畳まれたネットワークの単なる以前の実装です。 第1層l1の出力は、第2層の入力です。 新しいものは次の行にのみあります。

 l1_error = l2_delta.dot(syn1.T)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

l2からの予測の信頼度で重み付けされたエラーを使用して、l1のエラーを計算します。 寄与によって重み付けされたエラーが得られます。ノードl1の値によってl2のエラーへの寄与がどの程度なされるかを計算します。 この手順は、エラーの逆伝播と呼ばれます。 次に、2層のニューラルネットワークを使用したバージョンと同じアルゴリズムを使用してsyn0を更新します。