Clever Geek Handbook

MDAスペシャリスト向けの求人検索ガイド（および階層分析方法、XcoreとSiriusについて少し）





これは、モデル駆動型開発サイクルの記事4です。 以前の記事では、 OCLとメタモデル 、 Eclipse Modeling Framework、およびSiriusについて説明しました 。 今日は、メタモデルをテキスト表記（以前の図の形式ではなく）で記述し、Siriusのモデルの表形式表現に慣れる方法を学びます。 中年危機の例と階層分析法を使用してこれを行います。 これはおそらく、ゲームでAIを開発するとき、意思決定をするとき、または仕事でAIを開発するときに役立ちます。



はじめに



一般的に、DSL開発とモデル変換に関する記事を計画していました。 しかし、私の計画は突然、人生の意味、私が何かをしていたかどうかについての私の考えを混乱させました。



モデル駆動型開発の専門家ができる最も明白なことは





それが私たちのすることです。



マーキング



階層を分析する方法に興味があるが、メタモデルなどを理解したくない場合は、 Excel優先度計算機を利用できます 。






1階層分析方法



次の質問に興味がありました。





私が高校にいたとき、階層分析の方法を使用して、さまざまな質問への回答を得ました。 この方法の本質は次のとおりです。



  1. 定義します

    • 目標
    • 目標を達成するための基準
    • 可能な代替案。
  2. 基準の重要性を評価します。
  3. 各基準の代替案を評価します。
  4. 代替案の優先順位を計算します。
  5. 決定を下します。


この方法については、Thomas Saatiの著書「Decision Making」で詳しく説明しています。 階層の分析方法」（簡単にグーグルです）。 ところで、心理学から世界経済への多くの例があります。



1.1階層の構築


そのため、最も単純なケースでは、階層に目標、基準、および代替手段を含める必要があります。



すべての質問を要約すると、概して、転職すべきかどうかに興味があります。 したがって、目標は、仕事を選択することです。



仕事を選ぶとき、私は興味があります





次の選択肢があります。





階層分析方法に従って、次の階層が構築されます。







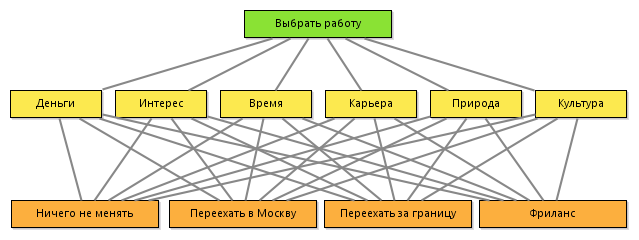
1.2基準の評価


意思決定の際に、異なる人々がほぼ同じ基準を持っている場合があります。 ただし、その重要性は大きく異なる場合があります。 誰かがお金のために、誰かが興味のために、誰かが同僚とコミュニケーションをとることを好む、などです。



彼らの優先順位に従って、ためらいのない一人はもっとお金のある仕事を選び、もう一人はもっと面白い仕事を選びます。 すべての基準で、すべての人に完全に適合する仕事はありません。



おそらく、決定を下すとき、ほとんどの人は明示的または暗黙的に基準を最も重要なものから最も重要でないものにランク付けします。 後者は破棄され、前者は可能な選択肢を比較します。 彼らはあらゆる可能性のある仕事にラベルを付けました：今、この仕事はより金銭的ですが、面白くありませんが、この面白くて集団はそこにありますが、疑わしいキャリアの見通しなど



すぐに選択できない場合、その人は基準を過大評価し始めます。おそらく、関心はまだそれほど重要ではなく、交通渋滞に2時間余分に耐えることができますが、より大きな給料があります。



そのような考慮事項は、最終的に最適な決定が実際に行われることを保証することなく、痛みを伴いながら長時間続く可能性があります。



階層分析法では、このような決定を行うための正式なアルゴリズムが提案されています。すべての基準は、1対9のスケールで互いにペアで比較されます。



たとえば、私にとってより重要なものは何ですか：興味またはお金ですか？ 関心はより重要ですが、そう言うことではありません。 最大スコアが9対1の場合、私にとっては優先順位を5対1として評価します。



または、例えば、どちらがより重要ですか：お金または生活のための時間の利用可能性、趣味？ 週末に余分なお金を払って仕事をする準備ができていますか？ 私は、これらの基準の重要性を1〜7として評価しています。



その結果、同様のテーブルが埋められます。







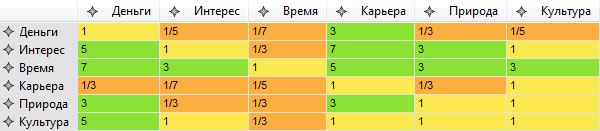
明らかに、対角線に沿って常にユニットが存在します。 また、すべての推定値が主対角に対して逆対称になることも明らかです。 たとえば、利子と金銭の重要度を5対1に評価すると、金銭と利子の重要度は1〜5になります。このような行列は逆対称と呼ばれることもあります。



一般的なケースでは、N個の基準を比較する場合、（N *（N-1））/ 2個の比較を行う必要があります。 すべてがより複雑になっているように思われます。 最初に6つの基準があった場合、いくつかの数値のマトリックス全体が存在することになります。 再び基準に戻るために、行列の固有ベクトルを計算します。 このベクトルの要素は、各基準の相対的な重要度になります。



トーマス・サーティの本は、心の中または紙の上で固有ベクトルを計算するためのいくつかの簡単な方法を提供しています。 より正確な反復アルゴリズムを使用します 。 



N =   m =    NxN eigenvector =   N,   1/N   eigenvalue               x = m * eigenvector eigenvalue = sum(x) eigenvector = x / eigenvalue


その結果、次のベクトルを取得します。 

 [ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]


最も重要な基準は時間（0.3846）であり、最も重要でない基準はキャリア（0.0555）です。



ペア比較では、推定値に一貫性がない場合があります。 たとえば、私にとって、興味はお金よりも重要であり、お金はキャリアよりも重要です。 明らかに、興味はキャリアよりもはるかに重要であるべきです。 この表は。 しかし、「利害関係のあるキャリア」の評価がそれよりも小さいか、あるいは反対である場合、私の推定値は互いに整合していません。



この不一致の尺度を評価することは、比較のマトリックスの独自の値に役立ちます。 6.7048に相当します。



明らかに、固有値は基準の数に比例します。 一貫性評価が基準の数に依存しないように、いわゆる一貫性インデックス=（固有値-N）/（N-1）が計算されます。



最後に、評価を完全に客観的にするために、このインデックスをランダム行列の平均一貫性インデックスに分割する必要があります。 取得した値（一貫性比）が0.1000未満の場合、ペアワイズ比較はほぼ一貫性があると見なすことができます。 この例では、0.1137です。これは、計算された優先順位が多少なりとも信頼できることを意味します。



1.3代替案の評価


ここで、各基準のすべての選択肢を比較する必要があります。







たとえば、モスクワに引っ越すと、給料から大きな恩恵を受けます。 しかし、この仕事は面白くないと思われ、人生の時間も短くなります。 または、海外に移動するときは、自分の言語を放棄し、他の人々の文化的価値に適応する必要があります。



各基準について、固有ベクトルと一貫性関係が計算されます。



結果の固有ベクトルは列に書き込まれます。







各基準の整合性関係は、次のベクトルに記録されます。 

 [ 0,0337; 0,0211; 0,1012; 0,1399; 0,1270; 0,9507 ]


ほとんどの値は0.1000より小さいか、わずかに大きいです。 しかし、「文化」という基準では、相関比は非常に大きいことが判明しました。 これは、評価の一部を誤って配置したためです。 あなたの故郷に住んでいるほうがずっと快適だからです。 しかし、誤って1/7に設定します。



1.4代替案の優先順位付け


そのため、基準を評価し、各選択肢にラベルを掛けました。どのオプションがより金銭的で、より興味深いかなどです。 次に、すべての基準の選択肢を合計して評価する必要があります。 これを行うには、単に行列を掛けます







ベクトルで 

 [ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]


その結果、次のベクトルが得られます。 

 [ 0,3184; 0,1227; 0,2049; 0,3540 ]


これらは、目標の達成に関する代替案の重要性です。



1.5意思決定


次の図にすべての計算値を示します。







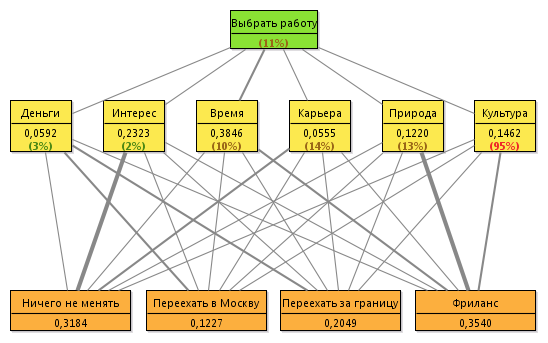
括弧内は、推定値の一貫性の関係を示しています。



線の太さは優先度に比例します。 キャリアの現在の仕事の面で最も興味深いと有望。 フリーランスは、より多くのものが自然に存在し、人生により多くの時間を費やすことを可能にするでしょう。 モスクワと海外でより多くのお金が働きます。



モスクワは完全に姿を消していることがわかります。 海外は少し良いですが、あまり良くもありません。 何も変更しないでください。フリーランスはほぼ同じレベルです。



2メタモデルの作成



次に、これらすべてがどのように描かれ、考慮されるかを説明します。



まず、メタモデル（階層分析方法で使用されるエンティティの種類）を説明する必要があります。 さらに、 前の記事とは異なり、メタモデルを図の形で描画するのではなく、Xcoreテキスト表記で説明します。



前と同様に、 Eclipse Modeling Toolsが必要になります 。 XcoreとSiriusをインストールします。



完成したプロジェクトを取るか、自分で行うことができます。 自分で作成した場合は、Xcoreプロジェクトを作成します。 モデルフォルダーで、次の内容のahp.xcoreファイルを作成します。 



 @Ecore(nsURI="http://www.example.org/ahp") @GenModel( modelName="AHP", prefix="AHP", editDirectory="/xctest.edit/src-gen", editorDirectory="/xctest.editor/src-gen", testsDirectory="/xctest.tests/src-gen") package ahp class Hierarchy { contains Goal[1] goal contains Criterion[+] criteria contains Alternative[2..*] alternatives } interface Named { String[1] name } class Goal extends Named { } class Criterion extends Named { } class Alternative extends Named { }


意味は直感的でなければなりません。 1つの目標、少なくとも1つの基準、2つ以上の選択肢を含む階層について説明しました。 3つのエンティティにはすべて名前があります。



ファイルを保存すると、src-genフォルダー内の階層を操作するためのJava APIが自動的に生成されます。 また、3つの追加プロジェクトが作成されます。 EMFについての記事で、すでに似たようなことをしました。 2つのモデル（ecoreとgenmodel）のみがあり、コード生成を手動で開始しました。 Xcoreはこれを自動的に行います。



記事でメタモデル全体を説明するのは意味がないと思うので、 自分で見ることができます 。



最も興味深いことだけを考えましょう。 Xcoreは、Ecoreとは異なり、モデルの構造だけでなく、Javaに似た言語でいくつかのロジックを記述することもできます。 たとえば、推定値を保存するためのデータ型について説明します。 正の推定値は正の整数として保存されます。 そして、フォーム1 / nの逆推定値は-nとして保存されます。 推定値を文字列または実数として保存できますが、これはおそらく悪い考えです。



その際、文字列表現との間で推定値を変換する2つの関数が必要です。 Xcoreでは、次のようになります。 



 type Weight wraps int create { if (it.matches("\\d+")) { Integer.parseInt(it) } else if (it.matches("1\\s*/\\s*\\d+")) { val result = Integer.parseInt(it.replaceFirst("1\\s*/\\s*", "")) if (result <= 1) 1 else -result } else { throw new NumberFormatException("The weight must be either n or 1/n") } } convert { if (it >= 1) { it.toString } else if (it >= -1) { "1" } else { "1/" + (-it).toString } }


Xcoreでは、比較的複雑なロジックを記述することもできます。

これは、たとえば、階層内の優先順位を計算する操作です。 
 class Hierarchy { op void updatePriorities() { priorities.clear inconsistencies.clear val mat = new JudgmentMatrix<Criterion>(criteria) val criteriaJudgments = judgments.filter(typeof(CriterionJudgment)).filter(cj | cj.goal == goal) for (judgment : criteriaJudgments) { mat.set(judgment.first, judgment.second, judgment.weight) } for (criterion : criteria) { val GoalCriterionPriority priority = AHPFactory.eINSTANCE.createGoalCriterionPriority priority.goal = goal priority.criterion = criterion priority.value = mat.findEigenvectorElement(criterion) priorities.add(priority) } val goalInconsistency = AHPFactory.eINSTANCE.createGoalInconsistency goalInconsistency.goal = goal goalInconsistency.value = mat.inconsistency inconsistencies.add(goalInconsistency) val mat2 = new Matrix(alternatives.size, criteria.size) criteria.forEach[criterion, j| val mat3 = new JudgmentMatrix<Alternative>(alternatives) val alternativeJudgments = judgments.filter(typeof(AlternativeJudgment)).filter(aj | aj.criterion == criterion) for (judgment : alternativeJudgments) { mat3.set(judgment.first, judgment.second, judgment.weight) } val criterionInconsistency = AHPFactory.eINSTANCE.createCriterionInconsistency criterionInconsistency.criterion = criterion criterionInconsistency.value = mat3.inconsistency inconsistencies.add(criterionInconsistency) alternatives.forEach[alternative, i| val CriterionAlternativePriority priority = AHPFactory.eINSTANCE.createCriterionAlternativePriority priority.criterion = criterion priority.alternative = alternative priority.value = mat3.findEigenvectorElement(alternative) priorities.add(priority) mat2.set(i, j, priority.value) ] ] val mat4 = mat2.multiply(mat.eigenvector) alternatives.forEach[alternative, i| val GoalAlternativePriority priority = AHPFactory.eINSTANCE.createGoalAlternativePriority priority.goal = goal priority.alternative = alternative priority.value = mat4.get(i) priorities.add(priority) ] } }




最後に、Xcoreモデル（およびEcoreモデル）について、クラス図を作成できます。







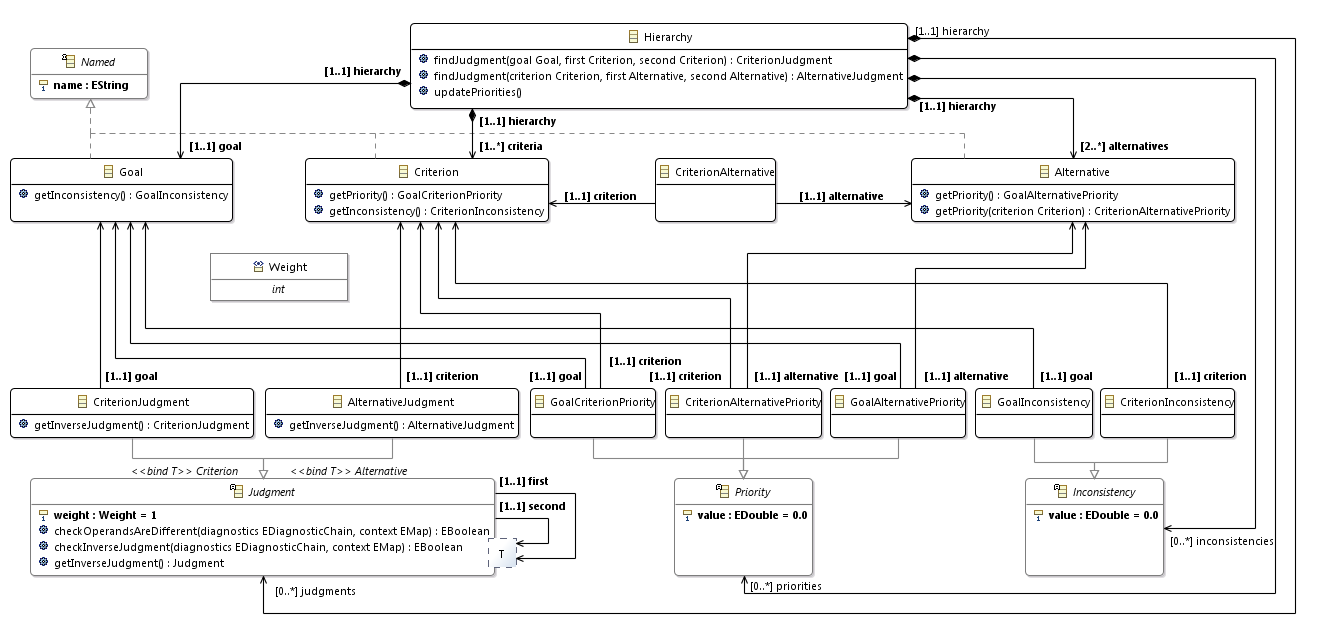
これは、階層分析メソッドのメタモデルです。 これは最も単純化されたオプションです。 一般に、階層には4つ以上のレベルを含めることができます（たとえば、基準にサブ基準を含めることができます）。 レベル間の関係の行列はまばらです。 評価は、1人だけでなく複数の専門家が行うことができます。



3モデルを操作するためのツールの開発



メタモデルの準備ができました。階層とマトリックス用のエディターが必要になりました。 これがどのように行われるかを詳細に説明する理由はおそらくないでしょう。 もし興味があれば、 シリウスに関する以前の記事を読んで、完成したプロジェクトを見ることができます。



これは、チャートおよびテーブルエディターの仕様がどのように見えるかです。







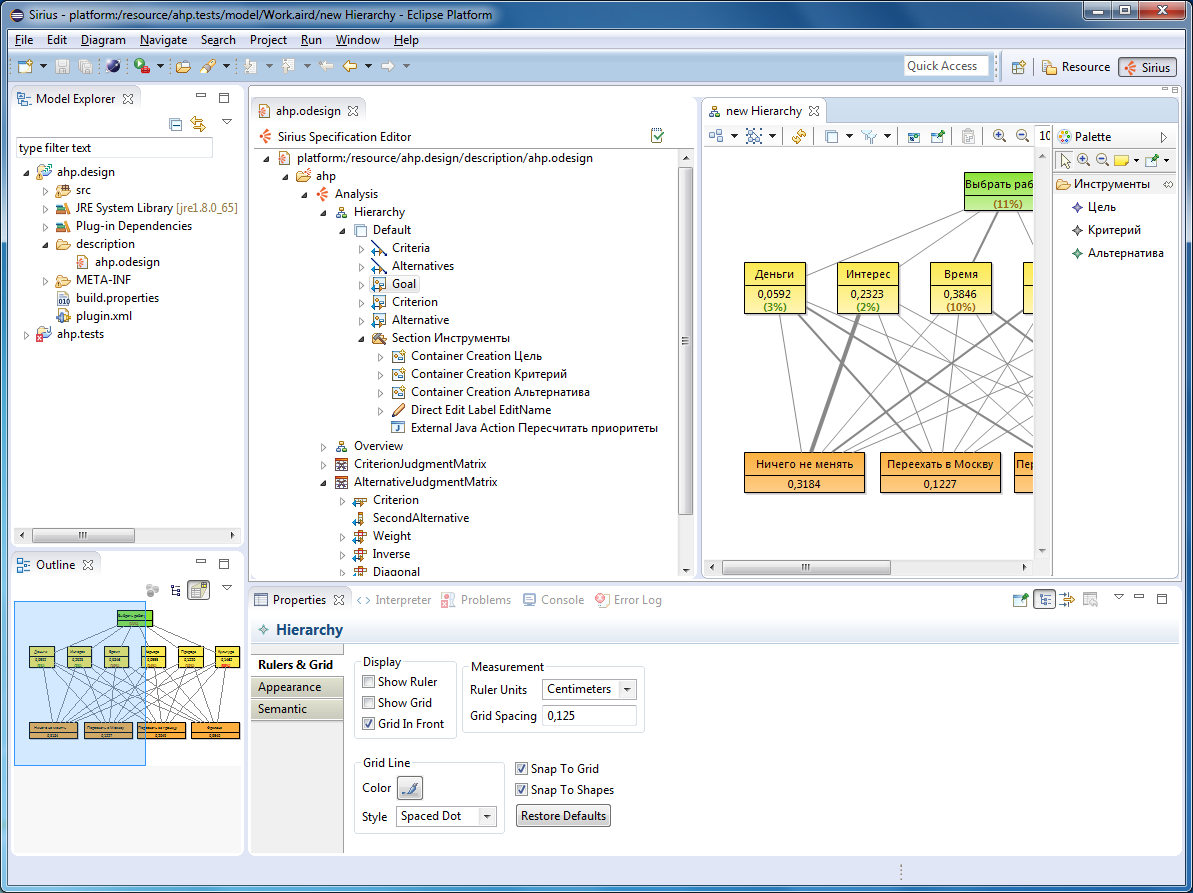
これは、結果のエディターの外観です。







階層エディターを記述することは完全に宣言的ではなく、Javaで拡張機能を記述する必要がありました。 これについてもう少し詳しく説明する価値があると思います。 Siriusには、サービスとアクションの少なくとも2つの拡張オプションがあります。



サービスを使用して、メタモデルからクラスにいくつかの追加操作を追加できます。 たとえば、次の2つの操作はそれぞれ優先度をフォーマットし、基準と代替案間のリンクの太さを計算します。 



 public class Service { public String toString(Priority priority) { return String.format("%.4f", priority.getValue()); } public int getEdgeWidth(Alternative alternative, EdgeTarget targetView) { DSemanticDecorator targetNode = (DSemanticDecorator)targetView; Criterion criterion = (Criterion)targetNode.getTarget(); Priority priority = alternative.getPriority(criterion); return (int) (priority.getValue() * 7); } }


便利なことに、これらの操作をAQL式で直接使用できます。 ただし、それらを使用してモデルを変更することはできません。



モデルを変更するには、Javaアクションを使用する必要があります。 サービスとは異なり、アクションはAQL式で呼び出すことはできません。 たとえば、コンテキストメニューから、またはボタンを押して起動できます。 [元に戻す]コマンドを使用して、アクションをロールバックできます。



階層内の優先順位を再集計するアクションの例。 
 package ahp.design; import java.util.Collection; import java.util.Iterator; import java.util.Map; import org.eclipse.emf.ecore.EObject; import org.eclipse.emf.transaction.RecordingCommand; import org.eclipse.emf.transaction.TransactionalEditingDomain; import org.eclipse.sirius.business.api.action.AbstractExternalJavaAction; import org.eclipse.sirius.business.api.session.Session; import org.eclipse.sirius.business.api.session.SessionManager; import org.eclipse.sirius.diagram.DSemanticDiagram; import ahp.Hierarchy; public class UpdatePrioritiesAction extends AbstractExternalJavaAction { public UpdatePrioritiesAction() { } @Override public boolean canExecute(Collection<? extends EObject> arg0) { return true; } @Override public void execute(Collection<? extends EObject> selections, Map<String, Object> parameters) { Iterator<? extends EObject> iter = selections.iterator(); if (!iter.hasNext()) { System.out.println("Selections is empty"); return; } EObject obj = selections.iterator().next(); if (!(obj instanceof DSemanticDiagram)) { System.out.println("DSemanticDiagram is expected"); } DSemanticDiagram diagram = (DSemanticDiagram)obj; EObject target = diagram.getTarget(); if (!(target instanceof Hierarchy)) { System.out.println("Hierarchy is expected"); } Hierarchy hierarchy = (Hierarchy)target; Session session = SessionManager.INSTANCE.getSession(target); TransactionalEditingDomain ted = session.getTransactionalEditingDomain(); RecordingCommand cmd = new RecordingCommand(ted) { @Override protected void doExecute() { hierarchy.updatePriorities(); } }; ted.getCommandStack().execute(cmd); } }




4モデルの作成



実は、実際にモデルを作成して上に示しました。 このプロジェクトを取り、階層を構築してみてください。



利益



この記事を読んだ後は、





More articles:


All Articles