
著者に敬意を表して、JavaScriptの例を含む記事の最後の部分はここでは公開しませんが、元のWebサイトで試してみることを提案します。 カットの下に、さまざまなシナリオの複雑なアリ最適化で利用可能な理論部分の翻訳があります。
Antコロニー最適化(ACO)は、1992年にMarco Dorigoによって最初に提案されました。 この最適化手法は、アリが順守する戦略に基づいて構築されており、食物を探す道を開いています。 さらに、ACOは群知能の特殊なケースです。 群知能は、分散型の集団行動を使用して問題を解決する一種の人工知能です。 Antアルゴリズムは、巡回セールスマンの問題を解決する場合など、組み合わせ最適化に最も広く使用されていますが、計画およびルーティングの分野のさまざまなソリューションとしても適用できます。
他の最適化アルゴリズムに対するアリアルゴリズムの重要な利点は、動的環境に適応する固有の能力です。 そのため、頻繁に変更が行われ、適応する必要があるネットワークルーティングには、これらが非常に不可欠です。
自然の中でアリ
ACOを完全に理解するためには、アルゴリズムの基礎となる、自然界でのアリの行動をよく理解することが重要です。
食べ物を検索するとき、アリは比較的単純なルールに従います。 すべての単純さのために、これらのルールにより、アリはコミュニケーションを取り、共同で獲物への経路を最適化できます。 これらすべてのルールの主な機能の1つは、フェロモントレースの使用です。 フェロモンの助けを借りて、一部のアリは食べ物がどこにあるのか、どうやってそこに行くのかを他のアリに伝えます。 原則として、アリがフェロモンの道をさまよう場合、彼はそこから食べ物を見つけると期待できます。 ただし、アリは最初のフェロモントレイルに沿って走りません。 その香りに応じて、アリは別の道を行くことも、フェロモンがないランダムな道を選ぶこともできます。 平均して、フェロモントレースの匂いが強いほど、アリがオンにすることを決定する可能性が高くなります。
時間が経つにつれて、他のアリがそれを更新しない場合、フェロモンのフットプリントは徐々に消えます。 したがって、食物につながらないフェロモンの痕跡は遅かれ早かれ放棄され、アリは新しい食物源への新しいルートを築かなければなりません。
このプロセスが時間とともにどのように発展し、コロニーがそれ自体の動作を最適化する方法を理解するために、次の例を検討してください。

これはアリが食べ物に行った方法です。 私たちの観点からは、この経路は明らかに最適ではありませんが、可能です。 しかし、ここから楽しみが始まります。 さらに、同じコロニーの他のアリは、最初のフェロモンの痕跡につまずきます。 それらのほとんどは元のルートに従いますが、一部は別のより直接的なルートを選択します:

この時点での最初のフェロモントレースはより香りが強いかもしれませんが、2番目のトレースは、アリが誤って方向転換する経路に対応して発達し始めます。 このシナリオでは、2番目のパスを選択することが重要です。これを選択する昆虫は、最初のパスをたどったアリよりも早く食物に到達し、それを得るためです。 たとえば、ある蟻は蟻塚から食料源への最初の経路に沿って3分を費やすことができますが、他の蟻は他の経路に沿って2倍速く走るので、そこに2つのフェロモントラックを残す時間があります。 このため、短いパスはすぐに最初のものよりも香りが強くなります。 したがって、最初のトレースは次第に使用されなくなり、最終的には消え、新しい短いパスのみが残ります。

このため、通常、最も厚いフェロモントレースが最も有利なルートに沿って堆積します。これは、特定の蟻塚のすべてのアリにとって次第に好ましいものになります。
これは、自然界でのアリの行動を単純化した図であることに簡単に注意してください。 さらに、さまざまな種類のアリがフェロモンを独自の方法で少し使用します。
アルゴリズム
この記事では、巡回セールスマンの問題を解決するためのACOアルゴリズムの適用について説明します。 このタスクの本質にまだ慣れていない場合は、記事「巡回セールスマン問題への遺伝的アルゴリズムの適用 」を参照してください。
ACOアルゴリズムの主要部分は、いくつかの段階のみで構成されています。 まず、コロニーの各アリは、既存のフェロモンの痕跡に基づいてソリューションを構築します。 さらに、解決されたソリューションの品質に応じて、アリは選択されたルートのセグメントに沿って痕跡を残します。 巡回セールスマン問題の例では、これらはエッジ(または都市間のパスのセグメント)になります。 最後に、すべてのアリがルートとフェロモントレースの敷設を完了すると、フェロモンは各セグメントで着実に蒸発し始めます。 その後、適切な解決策が得られるまで、この一連の手順が繰り返し実行されます。
ソリューション開発
前述のように、ルートを敷設するとき、アリは通常、最も臭いのあるフェロモントレイルに沿って走ります。 ただし、アリが現在最適と考えられている決定に加えて、他の決定を考慮し始めた場合、ランダム性の一部が意思決定プロセスに導入されます。 さらに、ソリューションのヒューリスティックな値が計算されて考慮されるため、最適なオプションに向かって検索が展開されます。 巡回セールスマン問題の例では、ヒューリスティックは通常、取得が計画されている次の都市までのエッジの長さに関連付けられています。 エッジが短いほど、ルートはそれに沿って続く可能性が高くなります。
これが数学的にどのように実装されるか考えてください:
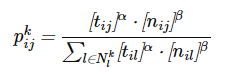
この方程式では、解の特定のコンポーネントを選択する確率が計算されます。 ここで、tijは状態iとjの間のフェロモンの量を意味し、nijはそのヒューリスティック値です。 αとβは、コンポーネントを選択する際のフェロモントレースとヒューリスティック情報の重要性を制御するパラメーターです。
コードでは、この情報は通常、ルーレットアルゴリズムのスタイルの選択肢として表されます。
rouletteWheel = 0 states = ant.getUnvisitedStates() for newState in states do rouletteWheel += Math.pow(getPheromone(state, newState), getParam('alpha')) * Math.pow(calcHeuristicValue(state, newState), getParam('beta')) end for randomValue = random() wheelPosition = 0 for newState in states do wheelPosition += Math.pow(getPheromone(state, newState), getParam('alpha')) * Math.pow(calcHeuristicValue(state, newState), getParam('beta')) if wheelPosition >= randomValue do return newState end for
巡回セールスマン問題のコンテキストでは、状態はグラフ内の特定の都市に対応します。 私たちの場合、アリは克服しなければならない距離と、このセグメントのフェロモンの量に応じて、次のアイテムを選択します。
ローカルフェロモンの更新
アリが成功したソリューションを受け取るたびに、ローカルフェロモン更新プロセスが呼び出されます。 このステップは、自然にいるアリが食物に向かう途中で残したフェロモンの跡の敷設をシミュレートします。 あなたが上記から覚えているように、アリはより速くそれらを克服するので、本質的に最も成功したルートはほとんどのフェロモンを受け取ります。 ACOでは、この特性は次のように再現されます。パスのセグメント上のフェロモンの量は、特定のソリューションがどれだけ成功したかによって異なります。 巡回セールスマンの問題を例にとると、フェロモンは総距離に応じて都市間の道路で遅れます。

この図は、典型的な巡回セールスマン問題のポイント(「都市」)の間に残ったフェロモンの痕跡を示しています。
コードでの実装を検討する前に、数学に目を向けます。

ここで、Ckはソリューションの総コストとして定義され、巡回セールスマン問題では、これは総パス長になります。 Qは、残っているフェロモンの量を修正するのに役立つパラメーターです。通常は1に設定されます。コンポーネント(i、j)を使用した各ソリューションのQ / Ckを合計し、この値はコンポーネントに残るフェロモンの量(i、 j)。
状況を明確にするために、巡回セールスマンの問題に関するこのプロセスの簡単な例を見てみましょう...
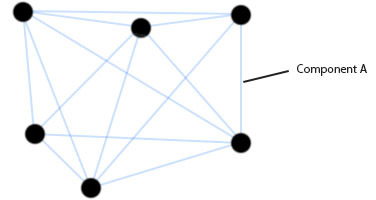
ここに、巡回セールスマン問題の典型的なグラフがあり、セグメントAにフェロモンがどれだけあるべきかを計算したいと思います。 また、3つのルートの合計長は次のとおりであると想定しています。
ツアー1:450
ツアー2:380
ツアー1:460
それらのそれぞれにフェロモンがどれだけあるべきかを計算するには、単に要約してください:
componentNewPheromone = (Q / 450) + (Q / 380) + (Q / 460)
次に、この値をセグメント上の既存のフェロモン値に追加します。
componentPheromone = componentPheromone + componentNewPheromone
次に、コードを使用した簡単な例を示します。
for ant in colony do tour = ant.getTour(); pheromoneToAdd = getParam('Q') / tour.distance(); for cityIndex in tour do if lastCity(cityIndex) do edge = getEdge(cityIndex, 0) else do edge = getEdge(cityIndex, cityIndex+1) end if currentPheromone = edge.getPheromone(); edge.setPheromone(currentPheromone + pheromoneToAdd) end for end for
この例では、コロニー全体のルートを繰り返し処理し、各ルートを抽出して、ルートの各エッジにフェロモン値を適用します。
グローバルフェロモンの更新
フェロモンのグローバル更新は、パスのセグメントからフェロモンが消える段階です。 このステージは、各アリがルートを正常に構築し、ローカル更新ルールを適用したときに、アルゴリズムの各反復後に適用されます。
グローバルフェロモンの更新は、数学的に次のように説明されます。
τij←(1 −ρ)⋅τij
ここで、τijは状態iとjの間のセグメント上のフェロモンであり、ρは揮発率を調整するパラメーターです。
コードでは、状況は次のように表すことができます。
for edge in edges updatedPheromone = (1 - getParam('rho')) * edge.getPheromone() edge.setPheromone(updatedPheromone) end for
最適化
ACOアルゴリズムでは、多くの最適化オプションを使用できますが、最も重要なものはエリート主義者とMaxMinです。 タスクによっては、これらのバリエーションは上記の標準のACOシステムよりも機能しやすい場合があります。 幸いなことに、これらの2つの変更を考慮するようにアルゴリズムを拡張することは難しくありません。
エリートバラエティ
エリートACOシステムでは、最も成功したアリのストリングとすべての最も生産的なアリは、他のすべてのアリよりもローカル更新の段階でフェロモンを少し多く残します。 したがって、植民地は、最高の成果の歴史を持つ人たちのモデルで行われた決定を適応させます。 すべてがうまくいけば、検索の品質が向上します。
数学的な観点から見ると、エリートのローカル更新手順は通常とほとんど同じですが、1つだけ追加されています。

ここで、eは、最適な(または「エリート」)ソリューションでデポジットされたフェロモンの追加量を修正するために使用されるパラメーターです。
マックスミン
MaxMinアルゴリズムは、「高評価」ソリューションを優先するという点で、ACOのエリートバージョンに似ています。 ただし、MaxMinはエリートソリューションに追加の重みを割り当てるだけでなく、最適なグローバルソリューションに対応する最も効率的な文字列にのみフェロモントレースを残すことができます。 さらに、MaxMinでは、フェロモントレースが特定の最小値と最大値の間の範囲内に収まる必要があります。 このアルゴリズムは、特定のトラック上のフェロモンの量が特定の範囲に属している場合、最適でないソリューションでの早すぎる収束を回避できるという考えに基づいています。
多くのMaxMin実装では、フェロモントレースを残すアリが最も成功していると考えられています。 次に、このアルゴリズムは、トレースを残す機能が「グローバルに」最高のアリでのみ保持されるように変更されます。 このプロセスは、最初は利用可能なスペース全体に分散している検索を刺激しますが、その後、最適なルートに焦点を当て、おそらく最小限の修正を可能にします。
最後に、最小値と最大値はパラメーターの形式で渡すか、コードで適応的に設定できます。
JavaScriptでのTSPの興味深い実用的なソリューション-著者のサイト