まえがき
これが私のモデルです。 私はそれを思いつき、プログラムで実装し、機能を研究し、説明しました。 彼女は、 「最大の類似性のサンプルの時系列を予測するためのモデル」というトピックに関する論文として、受け取った説明を擁護しました。 開発されたモデルは、 統計予測モデルのクラスに属し、同じシリーズの実際の値に基づいて時系列の予測を構築します。 私は以前に分類についてもっと書きました。 モデルの変更の 1つでは、予測に対する外部要因の影響を考慮することができます。
UPD 03/07/2019 : サンプルの更新版は、MATLAB 2015bで英語のコメント付きで入手できます 。
1.最大類似度のサンプルの予測モデルの説明
1.1。 時系列サンプルの基本的な考え方とその図
予測モデルの完全な正式な説明は、私の論文の第2章にあります。 ただし、簡単に言えば、このモデルは、歴史が渦巻き状に発達するという考え方に基づいています。段階は繰り返されますが、プロパティは変化します。
この考えを時系列に添付すると、これを言うことができます:時系列の実際の値には、それらがたくさんある場合、おそらく予測の前夜に起こることと非常に類似したセグメントがあります。
図 図1は、時系列Z(t)の一部を示しています。これについては、特別な計算を行わなくても同様のセグメントが顕著です。 タイムスタンプtで始まり、長さ(サンプル数)M、時系列のサンプル(時系列パターン)で始まる時系列のセグメントを呼び出し、Z M tを示します。
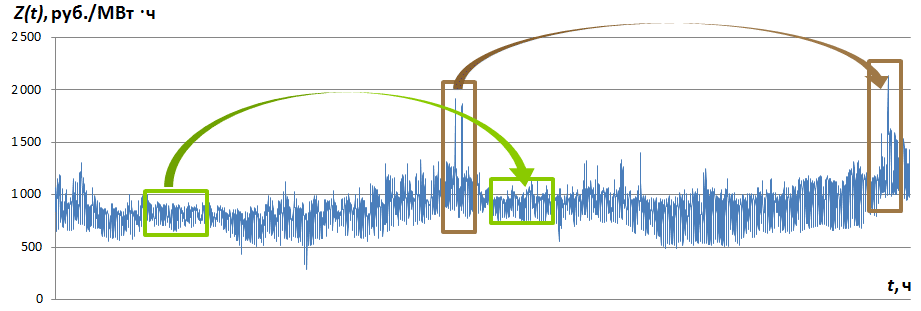
図 1.時系列Z(t)とそのサンプルの一部
すべての予測モデルは、いくつかの仮定に基づいています。 最大類似度サンプルモデルでは、履歴が繰り返される場合、予測に先行する各サンプルについて、同じ時系列の実際の値に含まれる類似のサンプルがあると想定されます。 正式には、これは類似性仮説と呼ばれます(論文を参照)。
サンプルの比率とその名前は図に見ることができます。 2。
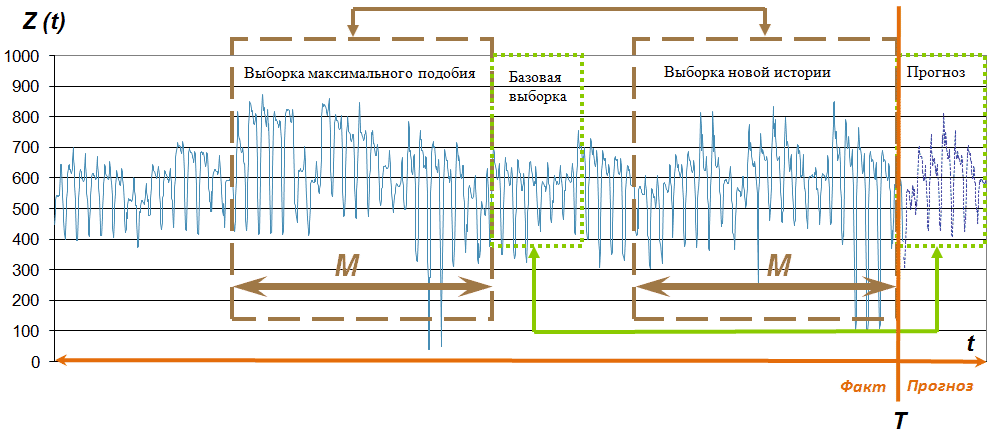
図 2.時系列のサンプルZ(t)
予測時間と呼ばれる時間Tで、将来の時系列のP値を決定する、つまり、 予測サンプルを計算する必要があります。 同時に、 新しい履歴サンプルの値も利用できます。 さらに、各サンプルに類似したものがあるという仮定に基づいて、 新しい履歴サンプルの最大類似性 サンプルを見つけ、履歴が繰り返される、つまり、 ベース サンプルが予測値の基礎になると仮定する必要があります。
次に、3つの質問に答える必要があります。
1.2。 サンプルの類似性を判断する方法は?
私の論文では、類似性を決定するための最も単純なオプション、つまり線形相関の値を計算することを提案しています。 長さMの1つのサンプルを取得し、長さMの別のサンプルを取得し、2つのサンプルの類似性を反映する相関値を考慮します。
検索最大の類似度のサンプルは、可能なすべてのサンプルを検索することで最も簡単です。 この種の最大100,000値の時系列の場合、パーソナルコンピュータで中程度の電力の実装を検索するには数秒かかります。
類似性を決定するために提案されたアプローチは、唯一可能なものではありません。 多くのフォロワーの学生が、2つのサンプルの類似性を判断する他の方法を作品で提案しました。 あなたの想像力をここで適用できます!
1.3。 プロパティの変更を「転送」する方法は?
線形相関が類似性を判断する基礎であるという事実により、サンプルのプロパティを「転送」するための最も簡単なオプションは線形依存です
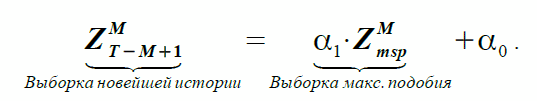 (1)
(1)
方程式(1)が係数α1およびα0を使用する2つの実際のサンプルの依存性を反映する場合、類似性の仮定に基づいて、予測と基本サンプルは次のように相関します。
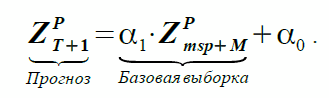 (2)
(2)
両方の式の係数α1とα0は同じですが、式(1)では不明であり、決定する必要があり、式(2)では既知です。 mspインデックスは、 最も類似したパターンを表します 。
英語のモデルの名前は、EMMSPと略される最も類似したパターンの外挿(または予測)モデルのように聞こえます。
1.4。 類似性の仮定は常に機能しますか?
これは、新しいタスクごとに確認する必要があります 。 時系列のすべてのモデルは、このシリーズを処理するためのツールであり、他のツールと同様に、モデルを適切に使用する必要があります。 大まかに言えば、ハンマーで釘を打ち、シャベルで地面を掘る必要があります。
開発したモデルは、価格とエネルギー消費量を予測する必要がある電力産業の分野で、時系列の短期予測のタスクで優れた結果を示しました。 このモデルは、財務時系列、血糖値などに関する他の予測モデルの結果に匹敵する結果を示しました。エラーの数値は、論文の第4章と 卸売電力および容量市場の予測指標に関する一連のレポートに記載されています 。
提案されたモデルの最も重要な特性は、そのシンプルさと明快さです。
2. MATLABの最大類似度のサンプルに対する予測モデルの実装例
予測モデルの例は、MATLABに実装されています。
2.1。 初期データ、予測問題のステートメント、およびモデルパラメーター
ソースデータは、2006年9月1日から2012年11月13日までの時間単位の解像度での卸売電力および容量市場のロシア連邦の欧州地域の電力価格/ MW•hの値です。 PRICES_EURアーカイブには、54,384個の値が含まれています。
この時系列の予測は、P = 24値先、つまり予測時刻の1日先T = 09/01/2012 23:00:00で計算する必要があります。
ソースデータのダウンロード:
% % , PRICES_EUR % <Date> - <Hour> - <Value> load PRICES_EUR PRICES_EUR; % PRICES_EUR.mat TimeSeries = PRICES_EUR;
予測問題ステートメント:
% T = datenum('01.09.2012 23:00:00', 'dd.mm.yyyy hh:MM:ss'); % (Origin) P = 24; % (Forecast horizon)
EMMSP予測モデルのパラメーター:
% M = 144; Step = 24;
この場合、 新しい履歴 サンプルと最大類似度サンプルの長さはM = 144です。 Mの決定方法については、論文の第3章を参照してください 。
Step変数は、 Maximum Similarity Sampleを決定するときに実際の値を列挙するステップです。
2.2。 最大類似度サンプルの予測モデルアルゴリズム
2.2.1。 新しい履歴の選択を定義する
Index = find(TimeSeries(:,1) == datenum(year(T), month(T), day(T)) & TimeSeries(:,2) == hour(T)); if length(Index) > 1 fprintf([' : T 1 \n']); elseif isempty(Index) fprintf([' : T \n']); else HistNewData = TimeSeries([Index-M+1:Index],:); % (HistNewData) Index = Index - Step * 2; end
2.2.2。 類似値を定義する
k = 1; while Index > 2 * M HistOldData = TimeSeries([Index-M+1 : Index],:); Likeness(k,1)= Index; CheckOld = find(HistOldData(:,3) > 0); % , CheckNew = find(HistNewData(:,3) > 0); if isempty(CheckOld) || isempty(CheckNew) Likeness(k,2) = 0; else Likeness(k,2) = abs(corr(HistOldData(:,3), HistNewData(:,3), 'type', 'Pearson')); end k = k + 1; Index = Index - Step; % Step end
列挙ステップStep = 24は、時系列に顕著な毎日の周期性があるという考慮から取られます。
2.2.3。 最大の類似度を決定する
MaxLikeness = max(abs(Likeness(:,2))); IndexLikeness = find(Likeness(:,2) == MaxLikeness); MSP = Likeness(IndexLikeness(1),1);
練習により、類似度の最大値がいくつかあることが示されています。 最初に取るのが最も便利です。
2.2.4。 最大類似度サンプルを定義する
MSPData = TimeSeries([MSP-M+1 : MSP],:); % (MSPData)
2.2.5。 基本サンプルを定義する
HistBaseData = TimeSeries([MSP+1:MSP+P],:); % (HistBaseData)
2.2.6係数α1およびα0の検索
% HistNewData MSPData . % . % , . X = MSPData(:,3); X(:,length(X(1,:))+1) = 1; % I Y = HistNewData(:,3); E = X(:,2); Xn = X'* X; Yn = X'* Y; invX = inv(Xn); A = invX * Yn; % alpha1 alpha0 A
係数α1およびα0の値を見つけた後、新しい履歴のサンプルが最大の類似度のサンプルに類似しているエラー、つまり式(1)のエラーを確認できます。 この例では、簡単にするためにテストは省略されています。
2.2.7。 予測
X = HistBaseData(:,3); X(:,length(X(1,:))+1) = 1; Forecast = X * A; % , 24
実装された例では、パラメータPを変更することにより、予測サンプルの数を変更できます。
2.2.8。 予測誤差の推定
% 1) Index = find(TimeSeries(:,1) == datenum(year(T), month(T), day(T)) & TimeSeries(:,2) == hour(T)); Fact = TimeSeries([Index : Index+P-1],3); % 2) MAE MAE = mean(abs(Forecast - Fact)); % 3) MAPE MAPE = mean(abs(Forecast - Fact)./Fact); fprintf([' T = ',datestr(T,'dd.mm.yyyy HH:MM'),'\n', ' P = ', num2str(P),'\n', ' MAE = ',num2str(MAE),' RUB/MWh, MAPE = ',num2str(MAPE*100),'%% \n']);
プログラムの実行結果に続いて、次のメッセージがMATLABコマンドラインに表示されます。
MaxLikeness = 0.95817 alpha1 = 1.0312, alpha0 = -11.1992 T = 01.09.2012 23:00 P = 24 MAE = 57.6383 RUB/MWh, MAPE = 6.0065%
ご質問は? ハブにアカウントをお持ちの場合はこちらから、お持ちでない場合はフォーラムでお問い合わせください。