素集合と神秘的なアッカーマン関数

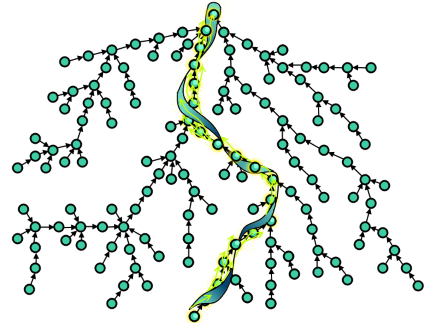
単純なデータ構造、つまり互いに素な集合のシステムについて話しています 。 要するに：互いに素な集合が与えられ（たとえば、グラフの連結成分）、2つの要素xとyによって次のことができます：1）xとyが同じ集合にあるかどうかを調べます。 2）xとyを含むセットを組み合わせます。 構造自体は実装が非常に簡単で、さまざまな場所で何度も説明されています（たとえば、 Habréやその他の場所に関する良い記事があります ）。 しかし、これは驚くほどのアルゴリズムの1つであり、費用はかかりませんが、効果的に機能する理由を理解することは容易ではありません。 2005年にZeidelとSharierによって発明された、このデータ構造の動作時間の正確な推定の比較的簡単な証明を提示しようとします（多くの人が他の場所で見ることができる恐怖とは異なります）。 もちろん、構造自体についても説明しますが、途中で、アッカーマンの逆関数とは何かを理解します。

ばらばらの集合システム

何らかの理由で、2つのクエリでn点のセットをサポートする必要があると想像してください。Union（x、y）は点xとyをエッジで接続し、IsConnected（x、y）は点xとyをチェックします。 xからエッジに沿ってyに渡すことは可能ですか？ そのような問題を解決する方法は？



まず、ポイントについてではなく、接続されたコンポーネントについて考えることが賢明です。 接続されたコンポーネントは、各ポイントから同じセットのエッジを相互に通過できるポイントのセットです。 Union（x、y）は、xとyを含むコンポーネントのユニオンです（同じコンポーネントにない場合）。IsConnected（x、y）は、xとyが同じコンポーネントにあるかどうかを確認するテストです。



第二に、ランダムに取得された特定の選択された頂点を各コンポーネントで選択すると便利です。 Find（x）は、xを含むコンポーネントから選択した頂点を返します。 Find（x）を使用すると、IsConnected（x、y）関数はFind（x）とFind（y）の単純な比較になります：IsConnected（x、y）==（Find（x）== Find（y）） Unionを使用して2つのコンポーネントを1つにマージすると、1つのコンポーネントで選択された頂点は常に1つであるため、結合されたコンポーネントの1つの選択された頂点は選択されなくなります。



したがって、元の問題から抽象化し、より一般的な別の問題の解決策に還元しました。Unionを使用して結合でき、Findを使用して取得した選択要素が含まれる、互いに素なセットのセットがあります。 正式には、構造は次のように説明できます。次の操作を含むシングルトンセットの初期セット{x ₁ }、{x ₂ }、...、{x _n }があります。

• Union（x、y）は、要素xおよびyを含むセットをマージします。
• Find（x）は、要素xを含むセットから選択された要素を返します。 xと同じセットからyを取得すると、Find（y）= Find（x）になります。 2つの要素が同じセットにあるかどうかを確認できるように、検索が必要です。

ばらばらのセットのシステム、またはむしろその実装は、後で説明しますが、コンピューターサイエンスのof明期に発明されました。 この構造は、Union-Findと呼ばれることもあります。 互いに素な集合のシステムには多くの用途があります：それらは最小スケルトンを見つけるためのクラスカルアルゴリズムで中心的な役割を果たし、いわゆるドミネーターツリー（コード分析の自然なもの）の構築に使用され、グラフ内の接続されたコンポーネントを簡単にたどります。 この記事には素集合セットの構造の実装の簡単な説明が含まれていますが、これらの構造の適用と実装の詳細については、 ハブとマキシム・イワノフですでに引用されているソースを読む方が良いとすぐに言わなければなりません。 しかし、ばらばらの集合のシステムの動作時間の異常な推定値がどのように取得されるかを知ることは、私にとって常に興味深いことでした。 したがって、この記事の主な目標は、Union-Find構造の有効性を理論的に正当化することです。



Union-Find操作でセットを実装する方法は？ 最初に思い浮かぶのは、セットを有向木の形で保存することです（図を参照）。 すべての木は多数です。 セットの強調表示された要素（Find関数が返す要素）は、ツリーのルートです。 ツリーをマージするには、あるツリーのルートを別のツリーにアタッチするだけです。







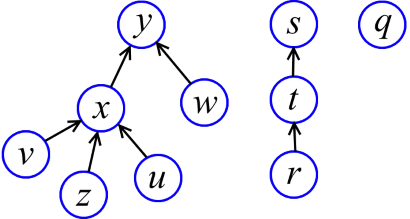
Find（x）は、xからルートに到達するまで矢印の方向に単純に上昇し、ルートを返します。 しかし、すべてをそのままにしておくと、Findが多くの時間を費やす「悪い」ツリー（長い「チェーン」など）を簡単に取得できます。 つまり、「背の高い」木は私たちを必要としません。



頂点x の高さは、リーフからxまでの最大パス長です。 たとえば、上の図では、高さy-2、x-1、z-0です。少し考えれば、各頂点に高さを設定できます。 これらの高さをランクと呼びます（将来的には、これらのことは高さとは予想されていません。将来、ツリーが再構築され、ランクが高さに正確に対応しなくなるためです）。 これで、2つのツリーが結合されると、下位のツリーが上位のツリーに固定されます（下図を参照）。







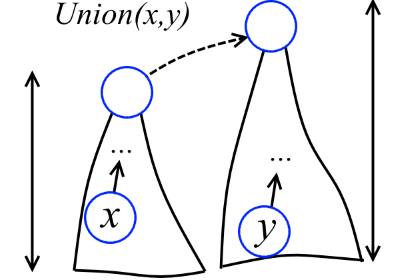
実現しました！ 次のように要素ノードを定義します。

struct elem { elem *link; //    int rank; //  double value; //-    };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初は、各要素xについて、x.link = 0およびx.rank = 0です。 ユニオン関数と予備関数のFind関数をすでに作成できます。

 void Union(elem *x, elem *y) { x = Find(x); y = Find(y); if (x != y) { if (x->rank == y->rank) y->rank++; else if (x->rank > y->rank) swap(x, y); x->link = y; } } elem *Find(elem *x) //   Find { return x->link ? Find(x->link) : x; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのような実装でさえ、すでに非常に効果的です。 これを見るために、いくつかの簡単な補題を証明します。



補題1.ランク最適化によるUnion-Find実装では、ルートxを持つ各ツリーには、≥2x- ^>ランク頂点が含まれます。



証明。 1つの頂点xで構成されるツリーの場合、x-> rank = 0であり、補題の主張が成り立つことは明らかです。 Unionが、補題の記述が真である根xとyで木を結合させます。 ルートxとyを持つツリーには、それぞれ≥2x- ^>ランクと≥2y- ^{>ランクの}頂点が含まれます。 xがyに結合し、yのランクが上がると問題が発生する場合があります。 しかし、これはx->ランク== y->ランクの場合にのみ起こります。 結合前のyのランクをrとします。 したがって、ルートyを持つ新しいツリーには、≥2x- ^>ランク + 2 ^r = 2 2 ^r = 2 ^{r + 1の}頂点が含まれます。 そして、これは証明するために必要でした。



補題2.ランク最適化を使用したUnion-Findでは、各頂点xのランクは、ルートがxにあるツリーの高さに等しくなります。



証明。 アルゴリズムが機能し始めたばかりで、すべてのセットがシングルトンである場合、各頂点x->ランク= 0、これは間違いなく高さです。 Unionが2つのツリーをルートxおよびyと組み合わせ、これらのツリーの高さが対応するランクx->ランクおよびy->ランクと正確に等しくなるようにします。 組合の後でも、ランクは高さに等しいことを示しています。 x->ランク<y->ランクの場合、xはyにフックされ、明らかに、ルートyを持つツリーの高さは変化しません。 Unionはy->ランクを実際に変更しません。 x-> rank> y-> rankの場合も同様です。 x-> rank == y-> rankの場合、xをyにアタッチすると、高さyが1増加します。 Unionはy->ランクを1だけ増やします。 必要でした。



補題1から、頂点のランクはlog n（2を底とするすべての対数を持っています）より大きくすることはできません。ここで、nは要素の数を示します。 また、補題2から、ツリーの高さはlog nを超えないことがわかります。 したがって、各検索操作はO（log n）で実行されます。 したがって、m個のUnion-Find操作はO（m log n）で実行されます。



さらに効率的ですか？ 2番目の最適化が助けになります。 Findプロシージャでアセントを実行する場合、単純にすべての頂点をルートにリダイレクトします（図を参照）。 確かに悪化することはありません。 しかし、はるかに優れていることがわかりました。

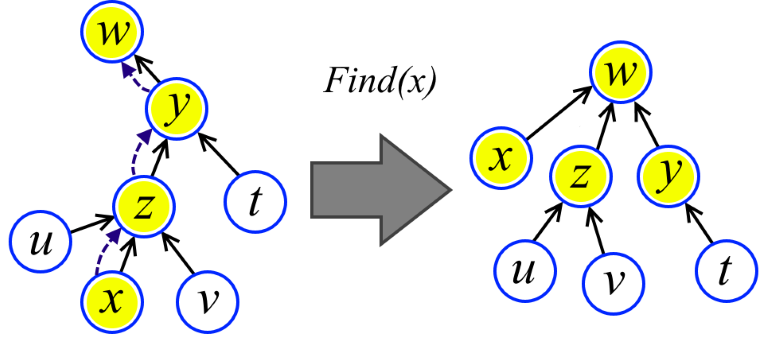
 elem * Find(elem *x) { return x->link ? (x->link = Find(x->link)) : x; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、n個の要素に対するm個のUnionおよびFind操作のシーケンスがあり、それが機能する時間を推定する必要があります。 O（m log n）でしょうか？ またはO（m log log n）？ それともO（m）ですか？



直感的には、2番目の最適化のアルゴリズムがより効率的であると思われます。 それはそうですが、それを証明するのはそれほど簡単ではありません。 少し分析すると、アルゴリズムは線形であると仮定できます。 UnionおよびFind shuffleのm個の操作のシーケンスはO（m）で実行されます。 しかし、どんな方法を試しても、そうではないので、これを厳密に証明することはできません。 正確な上限と下限の最初の完全な証明は1975年にTaryanによって与えられ、この境界は「ほぼ」O（m）でしたが、残念ながらO（m）ではありませんでした。 その後、原則としてO（m）を得ることが不可能であることが証明された研究が続いた。 正直なところ、私はすべてを理解することができませんでした。 Union-FindがO（m）より遅いことを示す反例でさえ、理解するのは非常に困難です。 しかし幸いなことに、2005年、サイデルとシャリールは上限の新しい「理解可能な」証拠を受け取りました。 彼らの記事は「パス圧縮のトップダウン分析」と呼ばれています。 ここで紹介するのは、少し簡略化された形式の結果です。 下限の「理解可能な」証拠を見つけることは、未解決の問題と見なすことができます。



O（m）と一緒に成長していないのはとても悪いですか？ 実際、Taryanによって取得された「ほぼ」O（m）は、考えられるすべての入力データのO（m）と区別できないため、これは純粋に理論的に興味深いものです（すぐに明らかになります）。 これがO（m）ではないという証拠はないことを私はすぐに言わなければなりません（私はそれを自分でまったく理解していません）。それで、あなたはまだ少しできるように思えるかもしれません...しかし、できません。 少なくとも、いくつかの試みが失敗したにもかかわらず、重大なエラーはTaryanの作品と一連の関連作品に見つかりませんでした。 著者「Union-Find Problem is Linear」の記事でよく知られている試みは、誤った引用です。「この論文には誤りがあり、撤回されました。 Citeseerから削除するだけです。 それを除けば、私はこの「訂正」を提出しています。

星、星、星

「ほぼ」O（m）を与える関数はどのような関数ですか？ すべてのn> 1に対してf（n）<nであるが、f（n）は無限大になる傾向があるような関数fを考えます。 関数fはゆっくりと成長します。グラフ全体が関数g（n）= nのグラフの下にあります。 スロー関数fからスーパースロー関数f ^*を作成する反復演算子*を定義します 。



f ^* （n）= min {k：f（f（... f（n）））<2、ここでfはk回取得されます}



つまり、f ^* （n）は、操作f（n）> f（f（n））> f（f（f（n）））> ...によって数nを圧縮する必要がある回数を示し、2未満の定数を取得します。



快適にするためのいくつかの例。 f（n）= n-2の場合、f ^* （n）= [n / 2]（2で割った整数部分）。 f（n）= n / 2の場合、f ^* （n）= [log n]（2進対数の整数部分）。 f（n）= log nの場合、f ^* （n）= log ^* nとは何ですか？ log ^* n関数は、 反復対数と呼ばれます。 紙に少し走り書きして、log ^* n = O（log log n）、log ^* n = O（log log log n）、および一般的にlog ^* n = O（log log ... log n）であることを証明できますログ。 反復対数がどれほど遅いかを想像するには、値log ^* 2 ⁶⁵⁵³⁶ = 5を見てください。



以下では、m個のUnion-Find操作の実行時間はO（m log ^* n）として推定でき、さらに推定O（m log ^** n）、O（m log ^*** n）および同様に、以下で定義されるある制限関数O（mα（m、n））まで。 一般に、現代の実用的なアプリケーションでは、O（m log log n）はO（m）とほとんど区別できません。 そして、O（m log ^* n）は一般にO（m）と区別できません。つまり、O（m log ^** n）などについて区別できません。 これで、「ほぼ」O（m）について話している理由が想像できます。

グレードO（m log ^* n）

O（m log ^* n）の推定値を取得することは、証明の重要な部分です。 その後、ほぼすぐに正確な推定値が取得されます。 簡単にするために、取るに足らない仮定を1つ作成します。m≥nです。



推論の一般性を制限することなく、Union操作は常に集合の「ルーツ」、つまり、 Unionは、Union（Find（x）、Find（y））のように呼び出されます。 その後、OでUnionが実行されます（1）。 Union（x、y）はまずFind（x）とFind（y）を呼び出すだけなので、この制限はより自然です。 したがって、分析では、検索操作のみに関心があります。



引き続き簡素化します。 検索操作がまったく実行されず、ユーザーが何らかの形でセットのルートがどこにあるかを推測すると想像してください。 一連の組合がフォレストFを構築します（フォレストは多くの木です）。 Fの補題2により、各頂点xのランクは、xをルートとするサブツリーの高さです。 したがって、各頂点のランクは、この頂点の親のランクよりも低くなります。 私たちにとって、この観察は重要です。



Findsのシーケンスをシステムに返しましょう。 最初の検索がFのパスに沿って実行され、F のパスを圧縮する操作を実行すると想像できます。パスの各頂点は、パスの「ヘッド」の頂点の子孫になります（図を参照）。 さらに、パスの先頭は必ずしもFのルートではありません。つまり、ある意味で、すべてのUnionが事前に実行され、フォレストFでは、Findに対応するパス圧縮がアルゴリズムの通常の過程で実行されることに同意します。 次に、2番目の検索は、変更されたフォレストに既にあるパスに沿って実行され（元のフォレストFでは、このパスはまったく存在しない場合もあります）、再びパスを圧縮します。 などなど。



パスの圧縮後、ランクは変更されないことに注意することが重要です。 したがって、変更されたフォレストでは、ランクが高さに対応しない可能性があるため、ランクを高さではなくランクと呼びます。







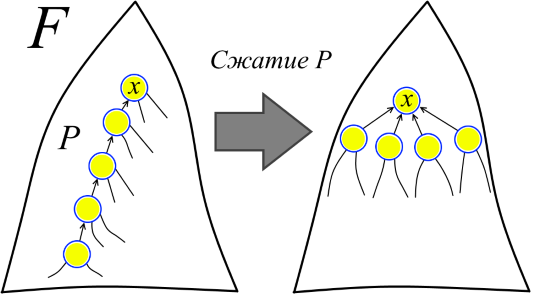
これで、証明していることを明確に述べることができます。 フォレストのシーケンスF = F ₁ 、F ₂ 、...、F _mと、それぞれフォレストF ₁ 、F ₂ 、...、F _mのパスP ₁ 、P ₂ 、...、P _mの圧縮のシーケンスがあります。 フォレストF ₁のパスP ₁の圧縮はフォレストF ₂を受け取り、F ₂のパスP _2の圧縮はF ₃を受け取ります。 （さらに、たとえば、パスP _kはフォレストFにまだ存在せず、パスP ₁ 、P ₂ 、...、P _k-1が圧縮された後にのみ出現する可能性_があります）パス長P ₁ 、P ₂ ...の合計を推定する必要があります、P _m （パスの長さはパス内のエッジの数です）。 圧縮可能なパスの長さは、対応するFindの頂点「リンク」操作の数にすぎないため、m回のFind操作の実行時間の推定値を取得します。



実際、パス圧縮のすべてのシーケンスがUnion-Findの一連の操作に対応するわけではないため、必要以上に一般的なステートメントを証明することに着手しました。 しかし、これらのニュアンスには興味がありません。



したがって、上記に関連付けられた意味で、フォレストFとその中のパスの収縮のシーケンスがあります。 フォレストのシーケンスF = F ₁ 、F ₂ 、...、F _mと、それらのパスP ₁ 、P ₂ 、...、P _mの収縮のシーケンスがあります。 T（m、n）は、長さP ₁ 、P ₂ 、...、P _mの合計が最大の場合、最悪の場合の圧縮可能パスP ₁ 、P ₂ 、...、P _mの長さの合計を示すものとします。 タスクは、T（m、n）を推定することです。 これは純粋に組み合わせの作業であり、Union-Findの有効性の自明でない証拠はすべて、この構造に何らかの形で自然に減少します。

圧縮可能なパスの長さの推定

議論の最初の本質的に重要なステップは、追加のパラメーターの導入です。 フォレストFのランクは、頂点Fのランクの中で最大です。T（m、n、r）により、T（m、n）と同様に、最悪の場合の圧縮可能なパスP ₁ 、P ₂ 、...、P _mの長さの合計を示します。長さP ₁ 、P ₂ 、...、P _mの合計_が最大で、ソースフォレストのランクがr以下である場合。 頂点がn個あるフォレストのランクはn以下であるため、T（m、n）= T（m、n、n）であることは明らかです。 パラメータrは、フォレストFの推定問題を下草Fのサブタスクに再帰的に削減するために必要です。



d = log rを示します。 フォレストFを2つのばらばらのフォレストF ⁺とF-に分割します。「上部フォレスト」F ⁺はランク> dのピークで構成され、「下部フォレスト」F-は他のすべてのピークで構成されます（図を参照）。 この分割は、次の事実に関連するUnion-Find推定の最初の証拠でさえ気づかれました：上位フォレストF ^+にはF-よりも著しく少ない頂点が含まれていることがわかります。



主なアイデアは、F ⁺にあるパス圧縮の長さを大まかに推定し（F ^+が非常に小さいためこれを行うことができます）、次にF-のパス圧縮の長さを再帰的に推定することです。 つまり、非公式には、再帰T（m、n、r）≤T（m、n、d）+（F-に含まれないパスの長さ）を導き出すことが目標です。 F ^+が 「非常に小さい」ことを意味するものを形式化することにより、この目標に向かって動き始めます。 で示す| F '| 任意のフォレストのピークの数F '。







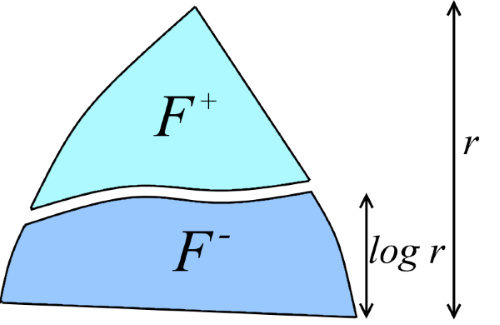
補題3. F ^+を 、ランク> dの頂点Fで構成されるフォレストとします。 その後| F ⁺ | <| F | / 2 ^d 。



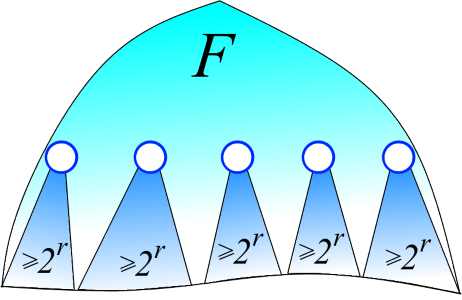
証明。 いくつかのt> dを修正します。 F ^+のランクtの頂点の数を推定してみましょう。 Fでは、補題2により、頂点のランクは、与えられた頂点にルートを持つツリーの高さに等しくなります。 したがって、ランクtの頂点の親は必ずランク> tになります。 したがって、ランクtのルートを持つサブツリーFは交差しません（下図を参照）。 補助定理1によるランクtのルートを持つツリーには、≥2 ^tの頂点が含まれます。 したがって、合計でランクtの≤n/ 2 ^tの頂点が存在します。 d + 1、d + 2、...に沿ってtを実行すると、F ⁺の頂点の数が無限の合計n / 2 ^{d + 1} + n / 2 ^{d + 2} + n / 2 ^{d + 3} + ...等比数列の総計公式により、この総計がn / 2 ^dであることがわかります。 必要でした。





ここからは、簡潔にするために、n ⁺ = | F ⁺ | およびn-= | F-|。



推論における重要な2番目のステップ。 パスのセットP ₁ 、P ₂ 、...、P _mを3つのサブセットに分割します（図を参照）。

• P ⁺ -完全にF ⁺に含まれるパス。
• P ^- F-に完全に含まれるパス。
• P ^+-は、F ⁺とF-の両方からの頂点を持つパスです。

セットP ^+-からの各パス^は 2つのパスに分割されます：F ^+の上のパス（左下の図の白い頂点）とF-の下のパス（左下の図の緑の頂点）。 上のパスを多数のP ⁺パスに配置しました。 このようにして得られたセット内のパス^の数をm ⁺で示します。 m ⁺ = | P ⁺ | + | P ^+- | （フォレストの同様の表記| F '|とは異なり、| P |はセットP内のパスの数を示し、それらの頂点の総数ではありません）。 m-= | P-|を示します。 次に：



T（m、n、r）≤T（m ⁺ 、n ⁺ 、r）+ T（m-、n-、d）+（P ^+-からのパスの下部の長さの合計）。







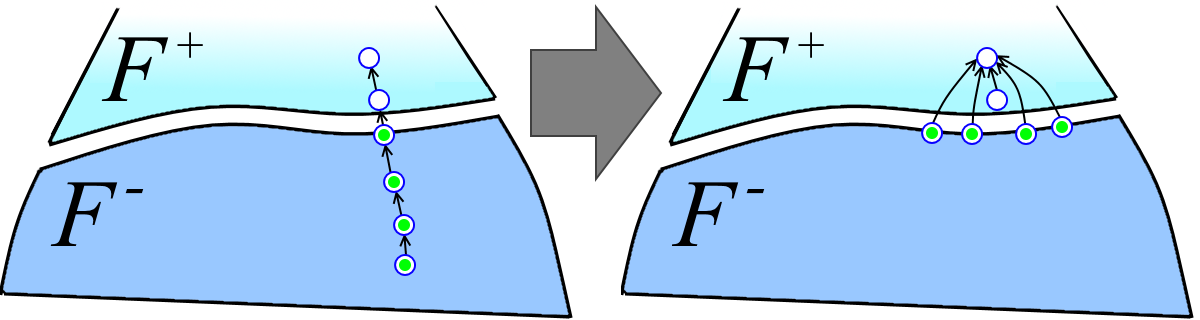
P ^+-からパスの下部の長さの合計を推定してみましょう。 PをP ^+- （上の図の緑の頂点）からのパスの下部とします。 ヘッド1を除くPのすべての頂点には、リンク前にF-からの親があり（リンク1には必ずF ⁺からの親があります）、リンク後はF ⁺からの親があります（上の図を参照）。 したがって、F-からの各頂点は、P ^+-からのパスの下位部分に1回だけ非ヘッドとして参加できます。 P ⁺からのパスの下部の長さの合計が| P ^+- |以下であることがわかります。 + n-（各頭の頂点に1つ、さらにF-の各頂点に1つ）。 | P ^+- | ≤m ⁺ 。 したがって、P ^+-からのパスの下部の長さの合計は、m ⁺ + n-を超えません。



重要な注意：議論では、Fのランクがd = log r以下であることは重要ではありませんでした。 log rの代わりに、他の値が存在する可能性があります。 あなたがこの場所に着いたら、おめでとう、中央補題を証明しただけです。



中央補題。 F ⁺をF>からの頂点のフォレスト、ranks> d、およびF ^- Fからの他の頂点^のフォレストとします。表記m ⁺ 、m-、n ⁺ 、n- ^は類推によって定義されます。 再帰は有効です：T（m、n、r）≤T（m ⁺ 、n ⁺ 、r）+ T（m-、n-、d）+ m ⁺ + n-。





すでに述べたように、F ⁺フォレストは非常に小さいため、その中のパスの長さは大まかな方法​​で推定できます。 やってみましょう。 明らかに、F ^+の長さkのパスの圧縮は、k-1頂点リンクを実行します。 つまり、k-1ピークがツリーを「上昇」します。 高さF ⁺はrを超えないため、各頂点はr回までしか上昇できません。 したがって、m ⁺パスの圧縮は、最大でrn ⁺再リンク（つまり、頂点を「登る」）を実行します。 このことから、F ^+の経路収縮の長さm ^+の合計は、数値rn ⁺ + m ⁺ （各頂点上昇に1つ、各経路の頭に1つ）によって上に制限されると結論付けます。 補題3により、rn ⁺ ≤rn / 2 ^d = rn / 2 ^{log r} = nが得られます。 その結果、T（m ⁺ 、n ⁺ 、r）≤n + m ^{+が得られ}ます。 中央補題を適用して、再帰を導きます：



T（m、n、r）≤T（m ⁺ 、n ⁺ 、r）+ T（m-、n-、log r）+ m ⁺ + n ^- ≤

≤n + m ⁺ + T（m-、n、log r）+ m ⁺ + n =

= 2n + 2m ⁺ + T（m-、n、log r）。



今、再帰的に、フォレストFで行ったのと同じように、フォレストFで同じように行動し続けます。 再帰を展開するだけです：

T（m、n、r）≤（2n + 2m ⁺ ）+ T（m-、n、log r）≤

≤（2n + 2m ⁺ ）+（2n + 2m ₀ ⁺ ）+ T（m _0- 、n、log log r）≤

≤（2n + 2m ⁺ ）+（2n + 2m ₀ ⁺ ）+（2n + 2m ₁ ⁺ ）+ T（m _1- 、n、log log log r）≤

≤...

ここで、m ₀ ⁺ 、m ₁ ⁺ 、...は、さまざまな再帰レベルでのm ^+に対応する値です。 m ⁺ + m ₀ ⁺ + m ₁ ⁺ + ...≤mであることは明らかです（下図を参照）。 再帰の深さは、定数を取得するためにrをプロローグする必要がある回数です。 しかし、これはlog ^* rです！ 結果として、T（m、n、r）≤2m + 2n log ^* rを導き出します。

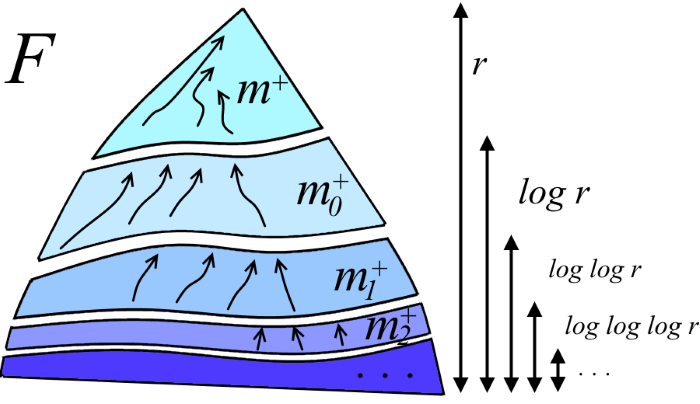
アッカーマンの逆最終ソリューション

調査結果を詳しく見ると、一般に、log rの値は式T（m ⁺ 、n ⁺ 、r）を展開してT（m ⁺ 、n ⁺ 、r）≤n + m ⁺ 。 これは、補題3とT（m ⁺ 、n ⁺ 、r）≤rn ⁺ + m ^+であることを証明する素朴な引数を使用して達成されました。 しかし、前のセクションでは、T（m ⁺ 、n ⁺ 、r）≤2m ⁺ + 2n ⁺ log ^* rのより良い推定値が得られました。 フォレストF-を「下げる」ことでメインキャラクターを再定義します。F ⁺は、ランク> log ^* rのピークFのフォレストであり、F-は、ランク≤log ^* rの残りのピークのフォレストです。 同様に、パラメータm ⁺ 、m-、n ⁺ 、n-を決定します。



補題3までに、n ⁺ <n / 2 ^{log * r}を取得し^ます 。 F ⁺フォレストは、F-に比べてまだ「小さく」なっています（最初は直感に反するように思えました）。 前のセクションでは、T（m ⁺ 、n ⁺ 、r）≤2m ⁺ + 2n ⁺ log ^* rであることを確立しました。 したがって、任意の整数x≥1に対して2（n / 2 ^x ）x≤nであることを考慮して、T（m ⁺ 、n ⁺ 、r）≤2m ⁺ + 2（n / 2 ^{log * r} ）log ^* r≤を導出します2m ⁺ + n。 これは、以前に得られた推定値T（m ⁺ 、n ⁺ 、r）≤n + m ⁺とほぼ同じです！ 中心補題を適用すると、再帰が得られます。



T（m、n、r）≤T（m ⁺ 、n ⁺ 、r）+ T（m-、n-、log ^* r）+ m ⁺ + n-。



T（m ⁺ 、n ⁺ 、r）≤2m ⁺ + nを開き、再帰を変換します。



T（m、n、r）≤T（m ⁺ 、n ⁺ 、r）+ T（m-、n-、log ^* r）+ m ⁺ + n ^- ≤

≤2m ⁺ + n + T（m-、n-、log ^* r）+ m ⁺ + n ^- ≤

≤3m ⁺ + 2n + T（m-、n、log ^* r）。



ここで、いくつかの再帰レベルを明らかにします。



T（m、n、r）≤（3m ⁺ + 2n）+ T（m-、n、log ^* r）≤

≤（3m ⁺ + 2n）+（3m ₀ ⁺ + 2n）+ T（m _0- 、n、log ^* log ^* r）≤

≤（3m ⁺ + 2n）+（3m ₀ ⁺ + 2n）+（2m ₁ ⁺ + 2n）+ T（m _1- 、n、log ^* log ^* log ^* r）≤

≤...



ここで、前のセクションと同様に、m ₀ ⁺ 、m ₁ ⁺ 、...は、さまざまな再帰レベルでのm ^+に対応する値です。 m ⁺ + m ₀ ⁺ + m ₁ ⁺ + ...≤mであることは明らかです。 再帰の深さはlog ^** rです。 その結果、T（m、n、r）≤3m + 2n log ^** r。 とても良いマークです。 しかし、このフォーカスは、取得したばかりの推定値T（m、n、r）≤3m + 2n log ^** rを使用してもう一度実行できますか？ はい！



詳細は今回省略します。 フォレストF-をlog ^** rのランクに「下げる」ことにより、再び補題3を使用してT（m ⁺ 、n ⁺ 、r）≤3m ⁺ + nを取得できます。 これは、T（m ⁺ 、n ⁺ 、r）≤2m ⁺ + nの推定値とほぼ同じです。 次に、この推定値と中央補題を使用して、T（m、n、r）≤4m + 2n log ^*** rを導き出します。



Fをログ^*** rのランクに「下げる」ことで、さらに続行できます。 一般に、正の整数kに対してこの手順をk回実行すると、次の推定値を取得できます。

T（m、n、r）≤km + 2n log ** ... * r、星の数はk-1です。

この繰り返し関係を最適化することは残っています。 星が多いほど、用語2n log ^{** ... *} rは小さくなりますが、kmは長くなります。 平衡は約kで達成されます。 しかし、我々はそれを決定します：用語n log ^{** ... *} rを2mに変えます。 この最終ステップの前に、rの代わりに、n-元のフォレストFのランクの上限を代入します（ただし、補題1により、r = log nになりますが、ポイントにはなりません）。 次の機能を導入します。

α（m、n）= min {k：n log ** ... * n <2m、星の数はk}。

関数α（m、n）は、アッカーマン関数の逆関数と呼ばれます 。 m≥nの場合にのみ関心があることを思い出してください。 α（m、n）の定義により、式n log ^{** ... *} n（α（m、n）の星）は2m未満です。 実際に、関数α（m、n）を導入して、最小限の星でそのような効果を取得しました。 たぶんこれはすぐに目立ったわけではないかもしれませんが、m個のUnion-Find操作がO（mα（m、n））で実行されることを証明しただけです。

タダム！

アッカーマンの逆関数について少し

逆アッカーマン関数を以前に見た場合、ほとんどの場合定義は異なっていました（よりわかりにくい）が、最終的には同じ関数を漸近的に与えました。Taryanが使用するAckermanの初期定義は、この機能について個人的には何も語りません（この場合、Ackermanが自分の機能を導入した地域では、定義は自然でした）。 ZeidelとSharirによって提案された（そして与えられたばかりの）定義は、逆アッカーマンの「秘密の意味」を明らかにしています。また、厳密に言えば、「アッカーマン関数の逆関数」は間違った名前です。なぜなら、α（m、n）は2つの変数の関数であり、いかなる関数に対しても「逆」にできないからです。したがって、α（m、n）はアッカーマンの擬似逆関数であると言われることがあります。アッカーマンの機能は提供しません。



少し分析します。最大α（m、n）は、m = nで達成されます。非常に小さな偏差でも（例：^m≥n log ^*****n）α（m、n）を定数にする。関数α（n、n）は、任意の数の星についてlog ^{** ... *} n よりもゆっくりと成長します。ところで、α（n、n）の定義は、反復の定義に似ています：



α（n、n）= min {k：log ^{** ... *} n <2、星の数はk}。



もちろん、これは制限ではなく、logα（n、n）のように、さらにゆっくりと成長する関数があります。別のことは驚くべきことです。α（m、n）は、このような自然なアルゴリズムの分析で発生します。さらに驚くべきことに、結果の推定値O（mα（m、n））を改善することは不可能であるという証拠があります。