本物のパーリンノイズを書く

検索クエリによって、Perlinのノイズは Habréでこの翻訳にすぐに出くわします。 出版物へのコメントで正しく指摘されているように、これはPerlinのノイズに関するものではありません。 おそらく、翻訳者自身が知らなかったのでしょう。



Perlinのノイズを有利に区別するものは、写真を比較すると簡単にわかります。



通常のノイズ（同じ記事から）：





パーリンノイズ：





そして、オクターブの数を増やすと、最初の画像を2番目の画像に近づけることができません。 Perlinノイズの利点とその範囲については説明しません（この記事はアプリケーションに関するものではなく、プログラミングに関するものであるため）が、その実装方法を説明しようと思います。 Ken Perlinのハッカーのソースはコメントがあってもあまり説明していないので、これは多くのプログラマーにとって役立つと思います。

リトリート

驚いたことに、PMと解説のレビューから判断すると、グレースケールの単純な滑らかなノイズとPerlinのノイズの違いを誰もがまったく見ることができないことが判明しました。 しかし、おそらく、この逆説のために、まさにその記事が登場し、人気がありました。



私はヒントを与えようとします：

最初の画像は、さまざまなグレーの濃淡の顕著なピクセル（拡大）で構成されています。



2番目（パーリンノイズ）は、白黒のぼやけたワームのように見えます。



グラフィカルエディターでの簡単な操作（境界線、反転、ポスタリゼーションの検索）の後に何が起こるかを次に示します。

パーリン：



記事の画像（まったく同じ操作が適用されます）：





はい、フラクタルノイズの場合、オクターブがたくさんあると、オリジナルの内容（Perlinであるかどうか）を理解するのは非常に困難です。 しかし、これはフラクタルノイズをPerlin Noiseと呼ぶ理由ではありません。

これは、違いの説明で終わります。

リトリートの終わり。



二次元オプションを考えてみましょう。 ここでは、空のクラスのみを記述します。 入力は、2次元ベクトルまたは2つの浮動小数点数、x、yです。



戻り値は-1.0〜1.0の数値です。

public class Perlin2d { public float Noise(float x, float y) { throw new NotImplementedException(); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

補間に関するいくつかの言葉

通常の平滑化ノイズの概念は、疑似ランダム値の離散グリッドがあり、要求されたポイントのグリッドノード間で補間が発生することです（ポイントがグリッドノードに近づくほど、その値はノード値に対応します）。



ここで、3番目の条件付き正方形では、補間後の中心のポイントの値は3になります。







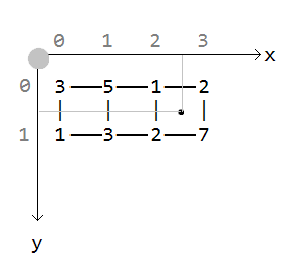
この3つがどのようになっているかをより詳しく考えてみましょう。 ポイント座標：

x:2.5,

y:0.5









ポイントの整数座標（正方形の左上隅）：

x:2,

y:0







切り捨てによって取得されます（フロア関数）。



正方形の内側の点のローカル座標は、減算によって取得されます。

x = 2.5 – 2 = 0.5,

y = 0.5 – 0 = 0.5









正方形の左上隅（1）と右上（2）の値を取得します。 ローカル座標x（0.5）を使用して上面を補間します。 線形補間は次のようになります。

 static float Lerp(float a, float b, float t) { // return a * (t - 1) + b * t;      ( ,    ): return a + (b - a) * t; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

正方形の左下隅（2）と右下（7）の値を取得します。 同じローカル座標x（0.5）を使用して底面を補間します。

結果：

: 1.5

: 4.5









これで、ローカルy座標（同じく0.5）を使用した上下の補間が残ります。

1.5 * 0.5 + 4.5 * (1 – 0.5) = 3









バイリニア補間は最も単純ですが、結果は最も魅力的ではありません。



他の補間オプションには、補間の前にローカル座標（パラメーターt）を変更することが含まれます。 境界値（0および1）の近くでより滑らかな遷移が得られます。







Perlinのノイズの中では、最初のオプションが関係しています。かなり強い曲率を与えます。

 static float QunticCurve(float t) { return t * t * t * (t * (t * 6 - 15) + 10); } ... //     : Lerp(a, b, QuinticCurve(t))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

パーリンノイズの主なアイデアと違い

すべてが非常に簡単です：

1.グリッドノードで、擬似乱数ではなく、擬似乱数ベクトル （2次元ノイズの場合は2次元、3次元の場合は3次元など）。

2. a）正方形の頂点から正方形内の点（3次元バージョンの立方体）へのベクトルとb）疑似ランダムベクトル（勾配ベクトルと呼ばれるPerlinノイズを記述する場合） のスカラー積の間を補間します。



改善されたバージョンのノイズでは、Ken Perlinは12個の勾配ベクトルのみを使用します。 2次元バージョンの場合、必要なのは4つだけです（面の数による）（正方形には4があります）。 ベクトルは（条件付きで立方体/正方形の中心から）各面に向けられ、正規化されません。



ここにあります：

 { 1, 0 } { -1, 0 } { 0, 1 } { 0,-1 }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、グリッドの各ノードは4つのベクトルのいずれかに対応します。 ベクトルをfloatの配列にします。

  float[] GetPseudoRandomGradientVector(int x, int y) { int v = // -   0  3      x  y switch (v) { case 0: return new float[]{ 1, 0 }; case 1: return new float[]{ -1, 0 }; case 2: return new float[]{ 0, 1 }; default: return new float[]{ 0,-1 }; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実装

ベクトルのスカラー積が必要です。

  static float Dot(float[] a, float[] b) { return a[0] * b[0] + a[1] * b[1]; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

主な方法：

  public float Noise(float fx, float fy) { //        int left = (int)System.Math.Floor(fx); int top = (int)System.Math.Floor(fy); //        float pointInQuadX = fx - left; float pointInQuadY = fy - top; //       : float[] topLeftGradient = GetPseudoRandomGradientVector(left, top ); float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top ); float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1); float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1); //        : float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY }; float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY }; float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 }; float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 }; //        /* tx1--tx2 | | bx1--bx2 */ float tx1 = Dot(distanceToTopLeft, topLeftGradient); float tx2 = Dot(distanceToTopRight, topRightGradient); float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient); float bx2 = Dot(distanceToBottomRight, bottomRightGradient); //   ,     : pointInQuadX = QunticCurve(pointInQuadX); pointInQuadY = QunticCurve(pointInQuadY); // , : float tx = Lerp(tx1, tx2, pointInQuadX); float bx = Lerp(bx1, bx2, pointInQuadX); float tb = Lerp(tx, bx, pointInQuadY); //  : return tb; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ボーナスとして：





最後の1つは、乱数を含むテーブルを使用することです。 Ken Perlinのコードでは、そのようなテーブルは手動で記述され、そこから値はまったく異なる方法で取得されます。 ここで実験することができ、ノイズの均一性と明示的なパターンの欠如はこれに大きく依存します。



やった









結果：