Qtの拡張現実

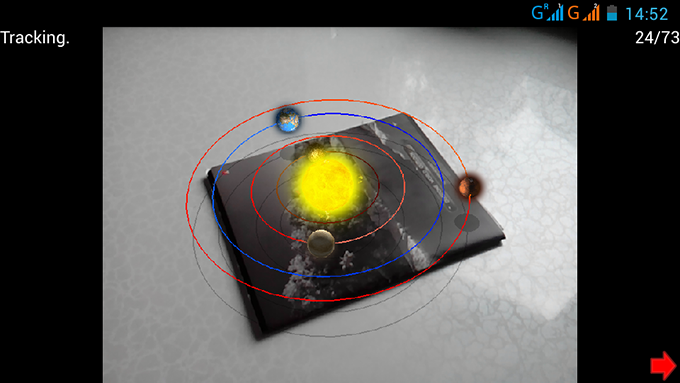
現在、拡張現実は最も興味深い分野の1つです。 したがって、私はその研究を始め、その結果は、Qtでのクロスプラットフォームマーカーレス拡張現実の独自の実装でした。 この記事では、どのように実装されたのか（または自分で実装する方法）について説明します。 カットの下では、githubでデモとプロジェクトへのリンクを見つけることができます。



拡張現実の操作にはマーカーは必要ありませんので、どんな絵でも必要です。 初期化を実行するだけで済みます。カメラを画像内のポイントに向け、開始ボタンを押して、選択したポイントの周りにカメラを移動します。

ここでは、WindowsおよびAndroidのデモをダウンロードできます （何らかの理由でWindows 10では機能しません）。

プロジェクトについて

プロジェクトは3つの部分に分かれています。

AR-拡張現実に関連するすべてがここにあります。 AR名前空間にはすべてが隠されており、ARSystemはシステムのメインオブジェクトであり、すべての計算が実行されます。

QScrollEngineはQtのグラフィックエンジンです。 名前空間にある-QScrollEngine。 githubには別のプロジェクトがあります。



アプリ-拡張現実システムとグラフィックエンジンを使用するアプリケーションについて説明します。

以下で説明するものはすべて、 PTAMおよびSVOプロジェクトに基づいています：Fast Semi-Direct Monocular Visual Odometry 。

入力データ

入力はビデオストリームです。 この場合、フレームからフレームへの情報があまり変化しない一連のフレームとしてのビデオストリームを意味します（これにより、フレーム間の対応を判断できます）。



Qtはビデオストリームを操作するためのクラスを定義していますが、モバイルプラットフォームでは機能しません。 しかし、あなたはそれを機能させることができます。 この記事では、これについては詳しく説明しません。

仕事の一般的なアルゴリズム

ほとんどの場合、拡張現実の作業では、空間内のカメラの位置を決定するのに役立ついくつかのマーカーが使用されます。 これはその使用を制限します。なぜなら、最初にマーカーがフレーム内に常にある必要があり、次に、最初にマーカーを準備（印刷）する必要があるためです。 ただし、代替手段があります。モーションテクニックの構造です。カメラの位置に関するデータは、ビデオストリームのフレームに沿って画像ポイントを移動することによってのみ検出されます。



すべての画像ポイントを一度に処理することは複雑ですが（かなり可能ですが（ DTAM ））、モバイルプラットフォームで作業するには単純化する必要があります。 したがって、画像内の個々の「特別な」ポイントを強調表示し、それらの動きを監視します。 「特別な」ポイントを見つける方法はいくつかあります 。 FASTを使用しました。 このアルゴリズムには欠点があります-特定のサイズ（9、10ピクセル）の角度のみを検出します。 異なるスケールのポイントを見つけるために、画像のピラミッドが使用されます。 つまり、画像ピラミッドは、最初の画像（ベース）が元の画像で、次のレベルの画像がサイズの半分である画像のコレクションです。 ピラミッドの異なるレベルで特異点を見つけると、異なるスケールの「特異」点が見つかります。 また、ピラミッド自体も光​​学ストリームで使用され、ポイントの軌跡を取得します。 あなたはそれについてこことここで読むことができます 。



したがって、ポイントの軌跡があり、今度は空間内のカメラの位置を何らかの方法で決定する必要があります。 これを行うには、アプリケーションから理解できるように、初期化は最初に2つのフレームで実行され、カメラは異なる角度でのみほぼ同じポイントに向けられます。 この時点で、これらのフレーム内のカメラの位置と「特別な」ポイントの位置が計算されます。 さらに、既知のポイントの3次元座標を使用して、ビデオストリームの次の各フレームでカメラの位置を既に計算できます。 より安定した操作を行うには、追跡プロセスに新しいポイントを追加して、カメラが見る空間の地図を作成します。

スクリーン座標に変換する

まず、「特別な」ポイントの3次元座標が画面座標にどのように移行するかを扱います。 これを行うには、次の式を使用します（式1と表記します）。



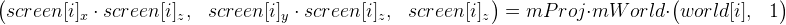
world [i] -これらは世界座標の「特別な」点です。 あなたの人生を複雑にしないために、これらの座標が全体を通して変化しないと仮定します。 初期化前は、これらの座標は不明です。

screen [i] -xおよびy成分は画像内の「特別な」点の座標です（それらは光束によって与えられます）。zはカメラに対する深さです。 これらの座標はすべて、ビデオストリームの各フレームで既に独自のものです。

mProjは3行3列の射影行列であり、形式は 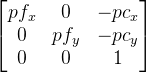、ここでpfはピクセル単位のカメラの焦点距離、 pcはピクセル単位のカメラの光学的中心です（通常は画像の中心付近）。 このマトリックスは、カメラのパラメーター（視野角）に対して形成する必要があることは明らかです。

mWorldは、サイズが3 x 4のポイントの変換を表すマトリックスです（つまり、最後の行が削除された通常のワールドマトリックス（ 0 0 0 1 ）から）。このマトリックスには、カメラの動きと回転に関する情報が含まれます。私たちは主にすべてのフレームを見ています。

この場合、 歪みは考慮されませんが、ほとんど効果がなく、無視できると想定しています。



マトリックスmProj （式1）を取り除くことにより、式を単純化できます。



。

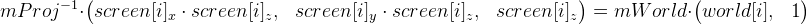
紹介します 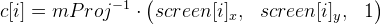事前に検討します。 次に、式1は、 （式2にします）。

初期化

すでに述べたように、初期化は2つのフレームで行われます。 それらをAおよびBとして示します。したがって、マトリックスがあります。 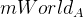そして 。 フレームAおよびB上の点c [i]は、 cA [i]およびcB [i]で示されます。 私たち自身が原点を自由に選択できるので、フレームAのカメラがちょうどそこにあると仮定します。したがって、 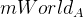単位行列です（3 x 4サイズのみ）。 そして、ここにマトリックスがあります まだ計算する必要があります。 そして、これは同じ平面にあるポイントの助けを借りて行うことができます。 次の式はそれらに有効です。

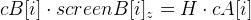ここで、行列Hは平面ホモグラフィです。

式を次のように書き換えます（わかりやすくするためにインデックスiを削除します）。







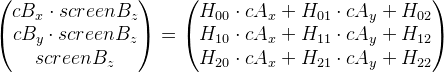
では、このビューに移り、削除します ：







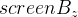行列Hをベクトルとして表す 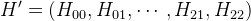、これらの方程式を行列形式で表すことができます。



。



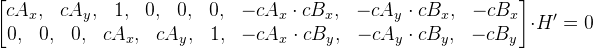新しいマトリックスをMとして示します。M* H ' = 0になります。これはすべて1点のみでペイントされたため、マトリックスMには2行しかありません。 行列H 'を見つけるには、行列Mの行数が列数以上である必要があります。 4つのポイントしかない場合は、ゼロの行を追加するだけで、9 x 9の行列が出力されます。次に、 特異分解を使用して、ベクトルH 'を見つけます（それ自体はゼロではありません）。 思い出すように、ベクトルH 'は行列Hのベクトル表現なので、この行列ができました。

しかし、上記のように、これはすべて同じ平面上にあるポイントにのみ当てはまります。 どれが配置され、どれが配置されていないかはわかりませんが、この方法でRansacメソッドを使用すると仮定できます。

1. ループ内で、所定の反復回数（たとえば500）で、次のアクションを実行します。
   
   
   • フレームポイントAとBの4つのペアをランダムに選択します。
   • 行列Hを見つけます。
   • 与えられた値よりも少ない誤差を与えるポイントの数、つまり 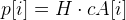そして、条件- 。
   
   
   
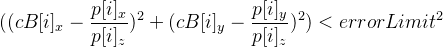2. ほとんどのポイントが判明した反復でHを選択します。

行列Hは、OpenCVライブラリの関数cvFindHomographyを使用して取得できます。



マトリックスHから、フレームAからフレームBへの位置遷移マトリックスを取得し、 mMotionと呼びます。

まず、行列Hの特異分解を実行します。 次の3つのマトリックスを取得します。 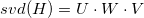。 いくつかの値を事前に紹介します。

-合計で±1に等しくなければなりません。











目的の符号を示す配列（ウェル、またはベクトル）：





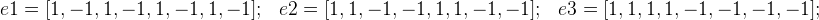
そして、 mMotionの 8つの可能なオプションをすでに取得できます。









;



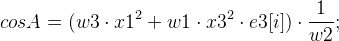
ここで、 R [i]は回転行列です。

t [i]は変位ベクトルです。



そして行列 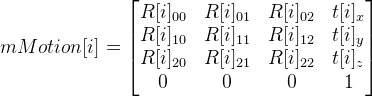。 パラメーターi = 0、...、7、およびそれに応じて、マトリックスmMotionの 8つのバリアントを取得します。

一般的に、次の関係があります。 = mMotion [i] * 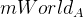以来 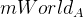-これが単位行列であることが判明 = mMotion [i] 。

8mi mMotion [i]から1つのマトリックスを選択することは残ります。 1番目と2番目のフレームのポイントからレイを解放する場合、最初の場合と2番目の場合の両方で、カメラの前で交差する必要があることは明らかです。 したがって、結果のmMotion [i]を使用して、最初と2番目のフレームでカメラの前にある交差点の数をカウントし、点の数が少なくなるオプションを破棄します。 最後にいくつかの行列を残して、エラーの少ない行列を選択します。

行列があります 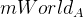そして 、それらを知ったので、それらの投影によって点の世界座標を見つけることができます。

複数の投影上の点の世界座標の計算

最小二乗法を使用することもできますが、実際には次の方法の方がうまく機能しました。

式2に戻ります。ポイント世界を見つける必要があります。 mWorld行列が既知（ mW [0]、mW [1]、...として示す）のフレームがあり、点aの投影の座標が既知（ [0]、[1]、...からすぐに取得）のフレームがあるとします 。

そして、次のような方程式系があります。





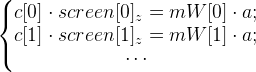
しかし、あなたはこの形でそれらを想像し、取り除く 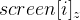（彼らが以前やったことと同様）：





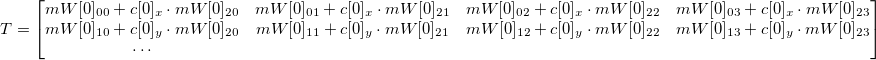
ここで、 sはゼロに等しくない任意の数です。

-行列形式の連立方程式。 T-既知、 f-はaを見つけるために計算する必要があります。

（ H 'を見つけたように）特異展開を使用してこの方程式を解くと、ベクトルfが得られます。 そしてそれに応じてポイント 。

点の既知の世界座標を使用したカメラ位置の計算

反復アルゴリズムが使用されます。 初期近似は、決定の以前の結果です。 各反復で：

1. 私たちはまだポイントです 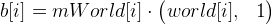。 理想的には、点c [i]は点b [i]と等しくなければなりません。現在の近似mWorldは近似（およびその他の計算エラー）だけであるため、それらは異なるためです。 このようにしてエラーベクトルを計算します。 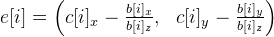。 最小二乗法により連立方程式を解きます。
   
   
   
   
   
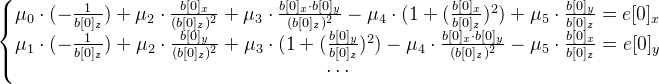
   必要な6次元ベクトルを見つける -ベクトル指数。
2. ベクトルから変位行列を見つける ：dT = exp_transformMatrix（mu）。
   
   
   この関数のコードは次のとおりです。

   TMatrix exp_transformMatrix(const TVector& mu) { // mu - 6-  TMatrix result(4, 4);//  4  4 static const float one_6th = 1.0f / 6.0f; static const float one_20th = 1.0f / 20.0f; TVector w = mu.slice(3, 3);//  3   mu TVector mu_3 = mu.slice(0, 3);//  3   mu float theta_square = dot(w, w);//dot -    float theta = std::sqrt(theta_square); float A, B; TVector crossVector = cross3(w, mu.slice(3));//cross3   2 3-  if (theta_square < 1e-4) { A = 1.0f - one_6th * theta_square; B = 0.5f; result.setColumn(3, mu_3 + 0.5f * crossVector);// 4   } else { float C; if (theta_square < 1e-3) { C = one_6th * (1.0f - one_20th * theta_square); A = 1.0f - theta_square * C; B = 0.5f - 0.25f * one_6th * theta_square; } else { float inv_theta = 1.0f / theta; A = std::sin(theta) * inv_theta; B = (1.0f - std::cos(theta)) * (inv_theta * inv_theta); C = (1.0f - A) * (inv_theta * inv_theta); } result.setColumn(3, mu_3 + B * crossVector + C * cross3(w, crossVector)); } exp_rodrigues(result, w, A, B); result(3, 0) = 0.0f; result(3, 1) = 0.0f; result(3, 2) = 0.0f; result(3, 3) = 1.0f; return result; } void exp_rodrigues(TMatrix& result, const TVector& w, float A, float B) { float wx2 = w(0) * w(0); float wy2 = w(1) * w(1); float wz2 = w(2) * w(2); result(0, 0) = 1.0f - B * (wy2 + wz2); result(1, 1) = 1.0f - B * (wx2 + wz2); result(2, 2) = 1.0f - B * (wx2 + wy2); float a, b; a = A * w(2); b = B * (w(0) * w(1)); result(0, 1) = b - a; result(1, 0) = b + a; a = A * w(1); b = B * (w(0) * w(2)); result(0, 2) = b + a; result(2, 0) = b - a; a = A * w(0); b = B * (w(1) * w(2)); result(1, 2) = b - a; result(2, 1) = b + a; }
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
3. マトリックスの更新 。

10〜15回の反復で十分です。 それでも、 mWorld値が目的の値にすでに十分に近い場合、ループから推測される追加の条件を挿入できます。

各フレームの位置を決定すると、いくつかのポイントが失われます。つまり、失われたポイントを探す必要があります。 また、焦点を当てることができる新しいポイントを検索するのに問題はありません。

ボーナス-三次元再構成

空間内の個々の点の位置を見つけることができるのであれば、空間内のすべての可視点の位置を決定してみませんか？ リアルタイムでは、これを行うには費用がかかりすぎます。 ただし、記録を作成して、後で再構築を実行できます。 実際、私はこれを実装しようとしました。 結果は明らかに完璧ではありませんが、何かが出てきます：







githubのソースコードにリンクします。



UPD： Windowsのバージョンを更新したため、以前のバージョンが機能しなかった場合、おそらくこれが機能するでしょう。 さらに、カメラを選択する機能が追加されました（複数ある場合）。