なぜこれが必要なのでしょうか？ たとえば、クレジットスコアリングを構築するときに、どの兆候がターゲット変数により依存しているかを理解するために-クライアントのデフォルトの確率を決定します。 または、私の場合のように、トレーディングロボットのプログラミングに使用する必要があるインジケーターを理解するために。
それとは別に、データ分析にc＃言語を使用していることに注意してください。 おそらくこれはすべてRまたはPythonで既に実装されていますが、c＃を使用すると、トピックを詳細に理解できます。さらに、これは私のお気に入りのプログラミング言語です。
非常に単純な例から始めましょう。乱数ジェネレーターを使用してExcelで4つの列を作成します。
X =ケース間（-100; 100）
Y = X * 10 + 20
Z = X * X
T =ケース間（-100; 100）
ご覧のとおり、変数Yは Xに線形に依存しています。 変数Zは Xに二次的に依存しています。 変数XとTは独立しています。 依存性の尺度を相関係数と比較するため、意図的にこの選択をしました。 ご存知のように、2つのランダム変数間で最も「ハード」なタイプの依存関係が線形である場合、1を法として等しくなります。 2つの独立したランダム変数の間にはゼロの相関がありますが、相関係数がゼロに等しいことから独立は続きません 。 さらに、変数XとZの例で確認します。
ファイルをdata.csvとして保存し、最初のフリークを開始します。 まず、数量間の相関係数を計算します。 私は記事にコードを挿入しませんでした、それは私のgithubにあります。 あらゆる種類のペアの相関を取得します。
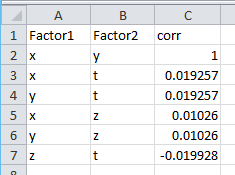
線形依存のXとYの場合 、相関係数は1であることがわかります。ただし、明示的な依存Z = X * Xを設定しても、 XとZの場合は0.01です。 明らかに、中毒をよりよく「感じる」手段が必要です。 しかし、カイ二乗基準に移る前に、共役行列とは何かを見てみましょう。
共役行列を作成するには、変数値の範囲を区間に分割します（または分類します）。 そのようなパーティションには多くの方法がありますが、普遍的な方法はありません。 それらのいくつかは、同じ数の変数を取得するように間隔に分割されますが、他は等長の間隔に分割されます。 私は個人的にこれらのアプローチを精神的に組み合わせています。 この方法を使用することにしました。変数からマットのスコアを引きます。 期待値、次に標準偏差推定による結果の配当。 言い換えれば、ランダム変数を中央揃えして正規化します。 結果の値は係数（この例では1）で乗算され、その後、すべてが最も近い整数に丸められます。 出力は、クラスの識別子であるint型の変数です。
したがって、記号XとZを取得し、上記のように分類してから、各クラスの発生数と発生確率、および符号のペアの発生確率を計算します。
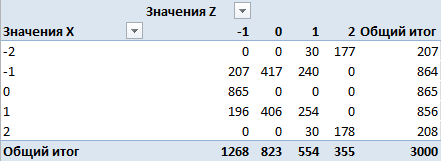
これは数量マトリックスです。 ここで、行は変数Xのクラスの出現回数、列は変数Zのクラスの出現回数、セルはクラスのペアの同時出現回数です。 たとえば、クラス0は変数Xで865回、変数Zで 823回発生し、ペア（0,0）はありませんでした。 すべての値を3000（観測の合計数）で割って、確率に目を向けます。
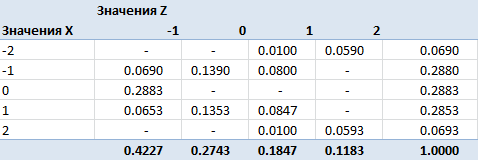
記号の分類後に得られた共役行列を取得しました。 次に、基準について考えます。 定義により、これらのランダム変数によって生成されるシグマ代数が独立している場合、ランダム変数は独立しています。 シグマ代数の独立は、それらからのイベントのペアごとの独立を意味します。 2つのイベントは、それらの同時発生の確率がこれらのイベントの確率の積に等しい場合、独立と呼ばれます： Pij = Pi * Pj 。 この式を使用して、基準を作成します。
帰無仮説 ：分類された特徴XとZは独立しています。 それと同等：共役行列の分布は、変数のクラスの出現の確率（行および列の確率）によってのみ決定されます。 または、マトリックスセルは、行と列の対応する確率の積です。 この帰無仮説の定式化を使用して、決定ルールを構築します。PijとPi * Pjの間の大きな不一致が、帰無仮説を拒否するための基礎になります。
させる
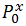-変数Xにクラス0が出現する確率。 合計で、 Xにはnクラス、 Zには mクラスがあります。 マトリックス分布を設定するには、これらのnおよびmの確率を知る必要があることがわかります。 しかし、実際には、 Xの n-1確率がわかっている場合、後者は1から他の合計を引くことで見つかります。 したがって、共役行列の分布を見つけるには、 l =（n-1）+（m-1）の値を知る必要があります。 または、1次元のパラメトリック空間があり、そのベクトルから希望の分布が得られます。 カイ二乗統計量は次のようになります。
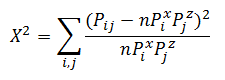
フィッシャーの定理によれば、自由度がn * ml-1 =（n-1）（m-1）のカイ二乗分布を持ちます。
0.95の有意水準を設定します（または、第1種のエラーの確率は0.05です）。 例（n-1）（m-1）= 4 * 3 = 12 ：21.02606982から、特定の有意水準と自由度のカイ二乗分布の分位を見つけます。 変数XおよびZのカイ二乗統計自体は4088.006631です。 独立仮説は受け入れられないことがわかります。 しきい値に対するカイ2乗統計量の比率を考慮すると便利です 。この場合、 Chi2Coeff = 194.4256186です。 この比率が1未満の場合、独立仮説が受け入れられ、それ以上の場合はいいえが受け入れられます。 すべてのサインのペアについて、この比率を見つけます。
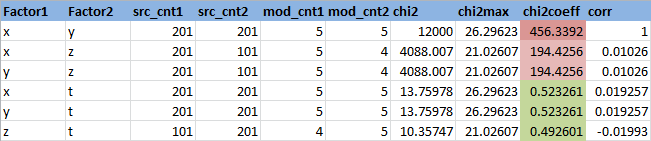
ここで、 Factor1およびFactor2は特性の名前です。
src_cnt1およびsrc_cnt2-ソースフィーチャの一意の値の数
mod_cnt1およびmod_cnt2-分類後の一意の特性値の数
chi2-カイ二乗統計
chi2max-有意水準0.95のしきい値カイ2乗統計
chi2Coeff-しきい値に対するカイ2乗統計の比率
corr-相関係数
変数Tはランダムに生成されるため、次の属性のペアが独立して取得されたことがわかります（chi2coeff <1）-（ X、T ）、（ Y、T ）および（ Z、T ）。これは論理的です。 変数XおよびZは依存していますが、線形依存のXおよびYよりも小さく、これも論理的です。
data.csvファイルと同じ場所で、これらのインジケーターを計算するユーティリティのコードをgithubに投稿しました。 ユーティリティはcsvファイルを受け取り、列のすべてのペア間の依存関係を計算します：PtProject.Dependency.exe data.csv
参照：
1. 独立仮説のテスト：ピアソンのカイ二乗検定
2. パラメトリック仮説をテストするためのピアソンカイ二乗検定
3. c＃での基準の実装