Clever Geek Handbook

止められない結合を伴うシステムの運動に関する問題における反作用と衝撃力の有限モデル

はじめに



この記事では、止められない接続を備えた機械システムの運動の問題を解決するための、型破りなアプローチを検討することを提案します。 このような問題を解決する場合、システムが通信から解放される条件を分析する必要があり、また、機械的衝撃の概念に密接に関連する通信に戻るときのシステムの動きの性質の変化を決定する必要があります。 そのような動きを形式化する方法の例として、簡単な問題を考えます



1.問題の声明



長さの固定された滑らかな水平スチールシリンダー内 L = 0.5 、m質量のある滑らかなスチールピストンがあります m = 2.0 kg ピストンは静止しており、コイルスプリングによってシリンダーの左端に押し付けられています。 c = 50 、N / m







図 1.ピストンの動きの問題の設計スキーム



バネには予圧がかかっています F_0 = 50 N.ある時点で t = 0 水平方向の力がピストンに作用し始めます \ vec P 法律によりモジュールが変更された人 P（t）= b \、t どこで b = 25 、N / s。 ピストンがシリンダーの前半を通過すると、力が \ vec P 動作を停止します。



ピストン運動の法則を見つけることが必要です x（t） 。 ピストンがシリンダーの左端に衝突したときの回復係数 k = \ frac {5} {9} 。



2.問題の数値および分析解



2.1。 ピストンが動き始める瞬間の決定



ピストンの運動の微分方程式を作成します



m \、\ ddot x = P-F_e + N






どこで F_e -バネの側面から作用する弾性力と等しい F_e = c \、x + F_0 ; N \ ge 0 -シリンダー端の側面から作用する反応。 私たちは方程式に来ます



m \、\ ddot x = b \、t-c \、x-F_0 + N






明らかに、ピストンの動きは、力が発生した時点でのみ開始されます \ vec P ばねの初期締め付け力を超える値に達する。 ピストンが静止していると仮定して、この瞬間を見つけてください



x = 0






式（2）は、シリンダーの動きを制限する制約を示しています。 （1）に（2）を代入すると、反応の大きさがわかります



N（t）= F_0-b \、t






ピストンの動きは一度に始まります t_1 シリンダーの端に圧力をかけるのをやめるとき、つまり N（t_1）= 0 。 ここから、動きが始まる瞬間を取得します



t_1 = \ frac {F_0} {b}






2.2。 力P （ t ）の作用下でのピストンの運動の法則



タスクデータに基づく t_1 = 2 、c。 で t＆gt; t_1 新しいカウントダウンを導入する \タウ そのような t = \ tau + t_1 式（1）は次の形式を取ります。



\ ddot x + \ omega_0 ^ 2 \、x = \ frac {b} {m} \、\ tau + \ frac {b} {m} \、t_1-\ frac {F_0} {m}






どこで \ omega_0 = \ sqrt {\ frac {c} {m}} -ピストンの固有振動数。 式（3）が与えられると、いくつかの単純化が得られます。



\ ddot x + \ omega_0 ^ 2 \、x = \ frac {b} {m} \、\ tau






この線形方程式の一般的な解の形式は



x（\ tau）= x_0（\ tau）+ x_p（\ tau）






どこで x_0（\ tau）= C_1 \、\ cos \ omega_0 \ tau + C_2 \、\ sin \ omega_0 \ tau -均一方程式の一般的なソリューション。 x_p（\ tau） 線形関数として求める不均一方程式の特定の解



x_p = A \、\ tau + B






（5）を（4）に代入すると、未知の係数AおよびBの方程式が得られます（5）



\ begin {align *}＆amp; B = 0、\\＆amp; \ omega_0 ^ 2 \、A = \ frac {b} {m} \ end {align *}






（6）を考慮すると、式（4）の一般的な解が得られます。



x（\ tau）= C_1 \、\ cos \ omega_0 \ tau + C_2 \、\ sin \ omega_0 \ tau + \ frac {b} {m \、\ omega_0 ^ 2} \、\ tau






で \ tau = 0 初期条件はゼロであり、そこから（7）の積分定数の値を決定します。



C_1 = 0、\クワッドC_2 =-\ frac {b} {m \、\ omega_0 ^ 3}






ようやく t＆gt; t_1



x_1（t）= \ frac {b} {m \、\ omega_0 ^ 2} \、\ left [t-t_1-\ frac {1} {\ omega_0} \、\ sin \ left（\ omega_0 \、（t -t_1）\ right）\ right]






数値的に超越方程式を解く



\ frac {L} {2} = \ frac {b} {m \、\ omega_0 ^ 2} \、\ left [t_2-t_1-\ frac {1} {\ omega_0} \、\ sin \ left（\ omega_0 \、（t_2-t_1）\ right）\ right]






瞬間を見つける t_2 ピストンがシリンダーの中央に達したとき。



t_2 = 2.564、\、\ rm c






2.3。 P （ t ）終了後の衝突前のピストンの動き



時間に t_2 力 \ vec P 終了し、ピストンの運動方程式は次の形式を取ります。



\ ddot x + \ omega_0 ^ 2 \、x =-\ frac {F_0} {m}






初期条件下でそれを解く x_1（t_2）= \ frac {L} {2} = 0.25、\ quad \ dot x_1（t_2）= v_2 = 0.974 解決策を得る t＆gt; t_2



x_2（t）= \左（\ frac {L} {2} + \ frac {F_0} {m \、\ omega_0 ^ 2} \右）\、\ cos \左（\ omega_0（t-t_2）\右）+ \ frac {v_2} {\ omega_0} \、\ sin \ left（\ omega_0（t-t_2）\ right）-\ frac {F_0} {m \、\ omega_0 ^ 2}






（9）から、ピストンが前方に移動することがわかります x _ {\ max} = 0.265 、m、そして反対方向に動き始め、一度にシリンダーの左端に当たります t_3 = 2.726 s スピードで v_3 = \ドットx_2（t_3）= -3.874 、m / s。



2.4。 シリンダーとの衝突後のピストンの動き



古典的な衝撃の理論によれば、身体が動かない障壁に対する共線的な衝撃の場合、回復係数の方程式



k =-\ frac {u_n} {v_n}






どこで k -回復係数; v_n -障害物への身体の導入速度の、その表面の法線上の投影; u_n -身体の速度の投影は、その表面の法線上の障害物から跳ね返ります。 したがって、最初の衝突後、ピストンは速度を上げます



u_1 = -k \、v_3






等式（8）に従い、 t＆gt; t_3 法律で動く



x_3（t）= \ frac {F_0} {m \、\ omega_0 ^ 2} \、\ left（\ cos \ left（\ omega_0（t-t_3）\ right）-1 \ right）-\ frac {k \ 、v_3} {\ omega_0} \、\ sin \左（\ omega_0（t-t_3）\右）






ある時点で t_4 次の衝突が発生し、その後、ピストンは法律に従って移動します。



x_4（t）= \ frac {F_0} {m \、\ omega_0 ^ 2} \、\ left（\ cos \ left（\ omega_0（t-t_4）\ right）-1 \ right）-\ frac {k ^ 2 \、v_3} {\ omega_0} \、\ sin \左（\ omega_0（t-t_4）\右）






n回目の衝撃の後、ピストンは法則に従って動きます



x_ {n + 2}（t）= \ frac {F_0} {m \、\ omega_0 ^ 2} \、\ left（\ cos \ left（\ omega_0（t-t_ {n + 2}）\ right）- 1 \右）-\ frac {k ^ n \、v_3} {\ omega_0} \、\ sin \ left（\ omega_0（t-t_ {n + 2}）\ right）






どこで t_ {n + 2} -方程式から決定される衝撃の瞬間 x_ {n + 1}（t_ {n + 2}）= 0 。



2.5。 ピストン運動則のグラフ



問題の初期データを考慮に入れて、得られた分析依存関係は、ピストンの座標の時間依存性のグラフを与えます







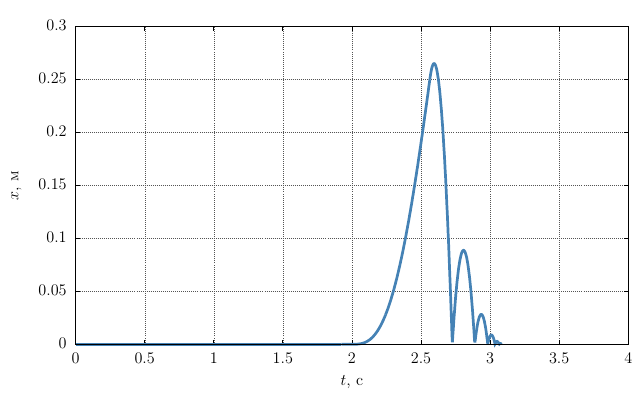
問題を解決する過程で、それがいくつかの異なる微分方程式がそれぞれ使用されるいくつかの段階に分割されることは明らかです。 さらに、代数方程式（10）を使用して、衝撃後のピストン速度を計算します。



通信から1つの詳細のみがリリースされ、それとの定期的な衝突が発生するかなり単純なシステムを検討します。 そして、そのような詳細がさらにあり、それらの運動の微分方程式と相互作用の性質がより複雑な場合はどうなりますか？ 上記の微分代数方程式をすべての場合に機能する1つの微分方程式に置き換えることは可能ですか？ できます。



3.衝撃力の非線形弾性粘性モデル



私たちのタスクでは、カップリング反作用は本質的に、ピストンがバリアに侵入するのを妨げる弾性力です。 衝突についても同じことが言えます。 文献は、それらのほんの一部だけが弾性変形の衝突を受けるという仮定に基づいたアプローチを説明しています。 このようなアプローチにより、下図に示すように、慣性力のない、一般的な場合、非線形力要素によって媒介される結合との衝撃および接触相互作用を記述することができます。







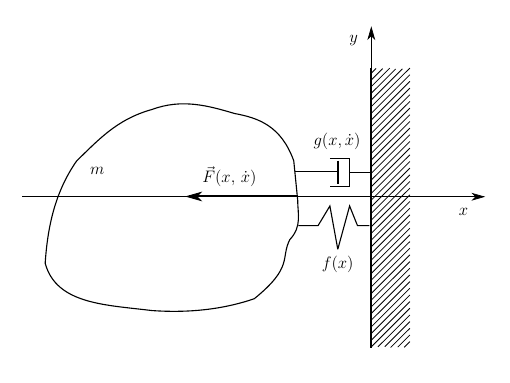
この場合、衝突プロセスは次の形式の微分方程式で記述できます。



m \、\ ddot x = -F（x、\、\ dot x）






衝撃力は、フォームの依存性によって記述されます



F（x、\、\ dot x）= \ begin {cases}＆amp; 0、\ quad x \ le 0 \\＆amp; S（x、\、\ dot x）、\ quad x＆gt; 0 \ end {cases}






この場合、衝撃の過程で、原点は障害物の表面に配置されます。 衝撃時のシステムの動作は、主に依存のタイプによって決まります S（x、\、\ドットx） 、さまざまな時間にさまざまな研究者によって行われた検索。 式を与える有名な線形ケルビン・ヴォイトモデル



S（x、\、\ dot x）= c_k \、x + \ beta \、\ dot x






どこで c_k -衝撃点での接触剛性; \ベータ -材料の粘度を考慮した散逸係数。 ただし、他のすべての欠点があるこのモデルでは、衝撃時の回復係数（10）は衝撃速度に依存せず、実験データと矛盾します。



作品では、 Borovin G.K.、Diagel R.V.、Lapshin V.V. 非線形粘弾性共線衝撃モデル衝撃力のモジュラスが式によって計算されるモデルに従って提案されます



S（x、\、\ dot x）= f（x）\、（1 + \ beta \、\ dot x）






どこで f（x） -弾性コンポーネント; \ベータ -材料の粘度を考慮した散逸係数。 （11）の弾性成分は、変形に線形に依存します。



f（x）= c_k \、x






衝突領域の表面が平坦で非線形の場合、準静的なヘルツモデルに従って



f（x）= c_k \、x ^ {\ frac {3} {2}}






凸面用。 モデル（11）は、非線形弾性粘性ハントクロスリーモデルと呼ばれます。 Borovin G.K.、Diagel R.V.、およびLapshin V.V.の研究は、Hunt-Crossleyモデルを使用した衝撃プロセスの詳細な分析研究を提供します。 モデル（11）を使用すると、回復係数の衝突速度への依存性が得られるという事実に言及することに限定されますが、これは実験データとよく一致しています。 下の図は、回復係数の衝突速度と係数への依存性を示しています \ベータ 。







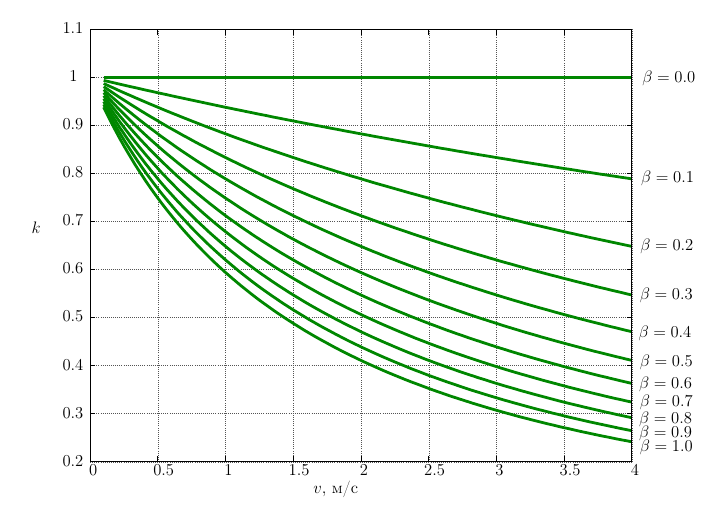
図 2.さまざまな散逸係数での衝突速度に対する回復係数の依存性



このモデルを使用して問題を解決してみましょう。



4. Hunt-Crossleyモデルを使用して数値的に問題を解決する



シリンダーの端面の反作用がアクティブな力の放出に伝達される場合、式（11）に基づいて、運動の微分方程式が得られます。



m \、\ ddot x = P（t、x）-c \、x-F_0 + N（x、\、\ dot x）






シリンダーが結合と相互作用する場合 x \ le 0 、シリンダー端の反応の式を書きます



N（x、\、\ dot x）= \ begin {cases} 0、\ quad x＆gt; 0 \\ -c_k \、x \、\ left（1-\ beta \、\ dot x \ right）、\ quad x \ le 0 \ end {cases}






このようなモデルは、静的接触下でのピストンとシリンダーの相互作用の性質をよく反映しています。（13）の速度がゼロに等しいという事実は、本質的に支持反作用である弾性力の表現を与えます。



問題の状態により、力 \ vec P（t） ピストンがシリンダーの中央を通過すると動作を停止するため、次の関数でこの依存性を定義します



P（t、x）= \ begin {cases} b \、t \ quad x＆lt; \ cfrac {L} {2}、\\ 0、\ quad x \ ge \ cfrac {L} {2} \ end {cases}






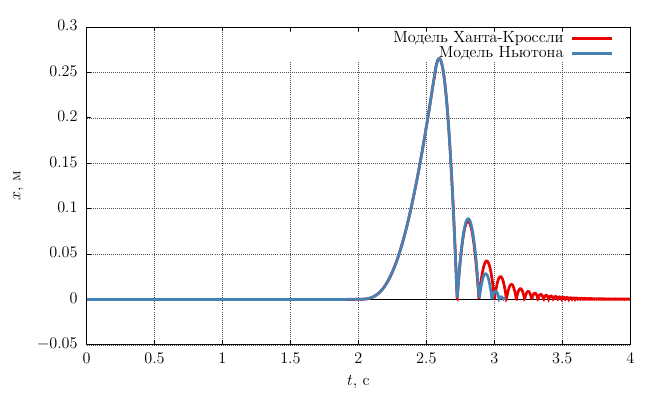
次のパラメーター値を受け入れます。接触剛性 c_k = 1 \ cdot 10 ^ {10} 、N / m; 問題で指定された回復係数に基づいて散逸係数を選択します k = \ frac {5} {9} 問題の分析解で私たちが取得した最初の衝突の速度（3.8 m / s）の推定- \ベータ= 0.31 （図2のスケジュールによる）。 初期条件がゼロの場合の数値積分により、分析とすぐに比較できる結果が得られます







また、衝撃力の連続モデル（13）を使用した問題の数値解は、2回目の衝突まで解析解と一致する解を与えることがわかります。 2回目の衝突後、衝突速度に対する回復係数の依存性が影響を受けますが、これは問題の分析解で使用した従来のニュートン衝撃モデルでは考慮されていません。 図2のグラフに基づいて、速度が低下すると回復係数が増加します。つまり、シリンダーの端からのピストンの「跳ね返り」の振幅は、分析ソリューションの場合よりもわずかに大きくなります。



係数付き \ベータ= 0.5 より速いピストン減衰が得られます







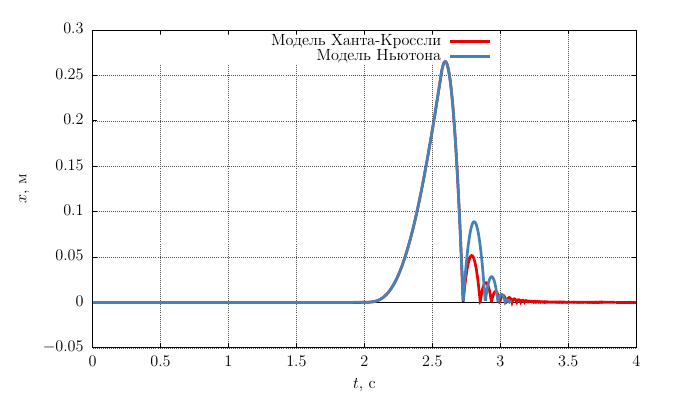
得られた結果は分析解と完全に一致しており、このシステムの運動を研究するために1つの微分方程式（12）のみが使用されていることに注意してください



結論



不安定な結合の反応をアクティブな力で置き換えることにある、私たちが検討したアプローチ（13）には否定できない利点があります。運動は微分方程式で記述されます。 システムの動きをインターバルに分割し、通信に戻るための条件を分析し、初期条件を「適合」する必要性から解放されました。 この問題の解決策は、時間間隔全体にわたってこの運動方程式系を連続的に積分することです。 これは、より複雑なメカニズムの動きの分析に特に当てはまります。



このアプローチの欠点は、式（12）の剛性です。 おそらく、接触剛性の非常に重要なことに気づいたでしょう。 これにより、 ODEシステムの数値積分のための特別な方法の使用が強制されます。特に、この場合、著者は5次のルンゲクッタフェルバーグ法を使用しました。 この方法には、変数の統合ステップがあり、時間に対する依存性は次のようになります







このグラフをソリューションのグラフと比較すると、ピストンが接続部に戻るとピッチが減少することがわかります。



いずれにせよ、このアプローチには存在する権利があり、さらなる研究により、その使用の正当性が示されます。



ご清聴ありがとうございました！


More articles:


All Articles