共役表：対数線形モデルとマルコフネットワーク

刊行物の前の部分では、非負行列の因数分解の方法は、次元の削減と分割表の視覚化として考えられていました。 このパートでは、取得したダイアグラムの統計分析を、対数線形モデルを使用して実行します。 念頭に置いて、複雑な調査データの例が示されています-層化、クラスター化、重み付けされたサンプル。 この状況には、モデルを評価および選択するための特別な方法の使用が含まれます。 得られた結果を視覚化するために、マルコフネットワークが使用されます。これは、対数線形モデルの因子の相互作用をグラフィカルに表現するための便利なツールです。











前のシリーズについて簡単に説明します。 2012年のESSデータによると、 「25〜40歳の男性」の一般人口について、調査対象国のそれぞれにおける人間の価値に対する支援の程度に関する表が作成されました。 表によって決定される29x21マトリックスの表示の次元を下げるために、ランク5のNMF変換が実行されました。











問題の声明

構築されたマップは、どの国（または国のクラスター）の間で、国（国のクラスター）からの価値変数の分配の独立性に関する仮説を拒否できるかを示唆しています。 発生する仮説を統計的に確認する必要があります。 例として、次の国のグループを使用します

• ロシアとスロバキア、階層的クラスタリングの結果によると-隣人;
• 異なる認識を持つ国のオプションとしてのフランスとロシア。

もちろん、選択はこれらの例だけに限定されず、研究者は自分の興味に合った国または国のクラスターを選択できます。

仮説を検証することに加えて、選択した国のグループに応じて価値要因はどのように相互作用するのかという疑問が生じます。 これらの可能な違いを識別することが必要です。



分割表について少し

NMF変換を実行するためのテーブル内のすべての値変数は、複数の選択肢を持つ単一の変数（複数応答変数）として認識されました。 これは、データを2次元テーブル、つまり2つの変数で形成されたテーブルの形式で表示するために必要でした。 実際には、状況は多少異なります。21の値変数の完全なセットと、国を示す1つの変数が22次元の分割表を決定します。

これはおそらく驚くべきことですが、統計モデルの構築の観点から見ると、多次元分割表（単一の応答変数を持ち、回答が欠落している）は、複数の応答変数を含む表よりも簡単な状況です。 さらに、NMFを使用すると、テーブルの次元が6-5潜在変数+ 1国の変数に縮小されました。



対数線形モデル

多次元分割表を分析する古典的な方法は、対数線形モデルを構築することです。 対数線形分析は、カイ二乗基準を多次元テーブルの場合に一般化したものと見なすことができます。 対数線形モデルの定義は、 Wikipedia（eng）で見つけることができます。 このトピックに関する資料は、ロシア語の例（ ここまたはここ ）、および英語の詳細な講義（ ここ）で利用できます 。



計算に進む前に、一般的なケースでは、多次元分割表が多項分布を決定することに注意してください。 しかし、1つの次元または複数の次元にわたるこの分布の周辺合計が固定されている場合、いわゆる積多項分布が得られます。 したがって、このようなテーブルの対数線形モデルのパラメーターに追加の制限を課す必要があります。 詳細は、本の第12章[1]に記載されています。 私たちの場合、限界額は一次元で固定されています-各国の人口の大きさは一定です。 これは、国の変数に対応する主効果をモデルから除外できないことを意味します。



最後のコメント。 調査データのどのテーブルがスパースであると見なされるかという質問は省略し、その結果、適切なチェックを行いません。



モデルの定義と比較

R環境の調査パッケージ[2]を引き続き使用して、層化、クラスタリング、およびサンプルの重み付けの影響を考慮します。 これは以前の出版物でより詳細に報告されました 。 複雑な調査データの対数線形モデルのパラメーターは、調査の設計を考慮しない場合のテーブルのパラメーターとまったく同じです。 モデルのパラメーターの有意性を計算する式の修正が必要です（個別および集合的に）。







例1 、最も単純なのは、ロシアとスロバキアのテーブルで、1つの潜在変数「money | 成功」。











2つのモデルを構築しています：因子の独立性と飽和を仮定しています。



飽和モデルは、独立性を仮定したモデルよりも大幅に優れているわけではありません。

つまり、テーブル内の変数の独立性に関する帰無仮説を拒否することはできません。

比較のために、これは独立モデルの結果を含む表です。











例2.フランスとロシアの5つの潜在変数すべてを含むテーブルを考えます。

すべての因子のペアごとの独立性を想定した対数線形モデルは拒否されます。 すべての2次要素を持つモデルは受け入れ可能です。 このモデルは単純化できます（また、そうする必要があります）-ワルドと尤度比の基準の結果により、国を決定する変数の2次パラメーターと最後の2つの潜在ヒートマップ変数が破棄されます。



条件付き独立。 数学のスキルと靴のサイズに依存する要因はなぜですか？

このバリエーションは古典的な例です。 回答者の数学的能力は、高、中、低の次のグラデーションによって決定されるとします。 たとえば、ロシア全土の人口について、これら2つの変数を使用して分割表を作成しています。 これらの変数の独立性の仮説は安全に却下できます。 靴のサイズが大きい人は、数学の能力が高くなります。 その理由は何ですか？ 隠された変数が存在しない場合、年齢。 ある時点まで、年齢は数学の能力と靴のサイズの両方と正の相関があることは明らかです。 年齢（ Age = k ）を固定すると、 kについて、 M （mat。Abilities）とS （靴のサイズ）の値の結合分布の表は、それらの間に有意な関係があることを示しません。 この場合、彼らは量MとSが条件付きで独立していると言います。 この結果は、自然にマルコフネットワークの形式で表現されます。これは、無向のグラフィカルモデルです。









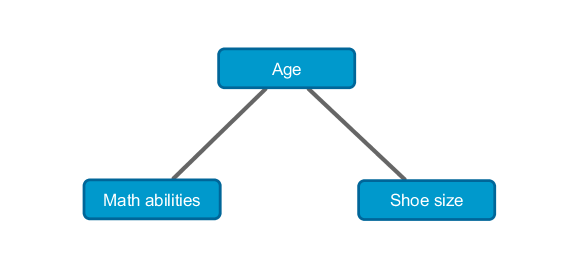
Habréには、ベイジアンネットワークに関する優れた記事があります-ダイレクトグラフィックモデルです。



対数線形モデルのグラフィカル表現

前の例を一般化して、[3]で実装された任意の階層ログ線形モデルに拡張することができます。 3つの変数A 、 B、およびCの一連のオプションを検討します。









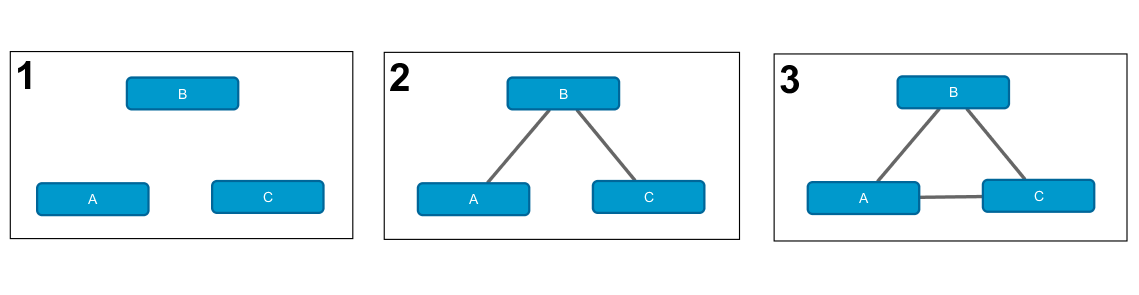
これらのマルコフネットワークは、次の対数線形モデルに対応します。







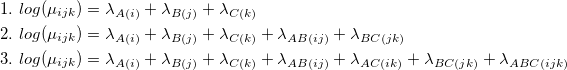
すべての階層対数線形モデルがマルコフネットワークとして表現できるわけではないことに注意してください。 たとえば、モデルAB / AC / BC 。 ただし、任意のモデルを最小限のマルコフネットワークに一意に埋め込むことができます。 対数線形モデルとグラフィカルモデルの対応の詳細は、本[1]または記事[3]に記載されています。



最終結果

マルコフネットワークは、変数の関係をナビゲートし、さまざまなテーブルの結果を比較することを比較的簡単にします。



















ロシアとスロバキアの場合、国と変数「冒険の探索は重要であり、リスクや楽しみの機会」との間に重要な関係があることがわかります。 他の値の品質では、Country変数は条件付きで独立しています。

一方、フランスとロシアでは、「金持ちになるか成功することが重要」、「楽しい時間を過ごすことが重要」、「シンプルで控えめであることが重要」という3つの声明に関して違いが顕著です。

これらの結論は両方とも、ヒートマップの結果と一致しています。

潜在変数間の関係に関しては、これらの国のペアのグラフは、1つのエッジだけが異なります。 ロシアとスロバキアの場合、「楽しい時間を過ごすことが重要」および「ルールに従うことが重要であるか、他者を助けることが重要」という変数は条件付きで独立しています。



結論として、複雑な調査データの対数線形モデルでは、AICまたはBICの結果に基づく段階的なモデル選択はまだ実装されていないことに注意してください。 このようなデータにこれらの基準を適合させた記事は、最近になってようやく登場し始めました。 特に、今年の記事は[4]で、共著者の1人は調査パッケージの作成者であるT. Lumleyです。



参照：

[1] G. Tutz（2011）カテゴリーデータの回帰、ケンブリッジ大学出版局。

[2] T. Lumley（2014）調査：複雑な調査サンプルの分析。 Rパッケージバージョン3.30。

[3] JN Darroch、SL Lauritzen、およびTP Speed（1980）分割表のマルコフ場と対数線形相互作用モデル。 統計学8（3）、522-539。

[4] T. Lumley、A。Scott（2015）AICおよびBIC、複雑な調査データを使用したモデリング、J。Surv。 統計 方法 3（1）、1-18。