Datawiz.ioでは、いくつかのオタクを集めて、現在の状況を変えようとすることにしました。 あなたの知識を、現実的で、測定可能で、さらには社会にとって有益なものに使用するのは興味深いことです。 小売業界に立ち寄った。 小売店は、処理のための多くのデータを提供します。販売、小切手、価格設定、顧客、ロイヤルティプログラムなど、数字の滝です。
小売データの単純な視覚化も非常に退屈です。 従来の分析では昨日のデータを表示でき、レポートでは見栄えがよくなりますが、明日は表示されません。
機械学習モデルの動作は異なります。 彼らはあなたに制御と相互作用を与えます。 モデルで遊んだり、パラメータを変更したり、それが結果にどのように影響するかを確認したり、さまざまな要因の組み合わせの結果を調査したりできます。 オラクルとのコミュニケーションではないものは何ですか?
簡単なものから始めましょう。
どの商品の売上が店舗の総収益に影響するかを判断することは可能ですか?
2つの店舗の初期データがあります。食料品店とスーパーマーケットと呼びましょう。
1.特定のカテゴリの商品の販売。
2.特定のカテゴリの商品の受領における言及の数。
テーブルを作成します。
行-週;
列-カテゴリー;
セル-販売されたアイテムの数またはレシートへの参照。
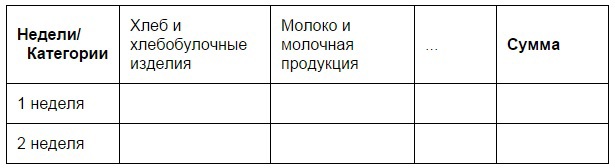
合計-4つのテーブル、各ストアに2つ。
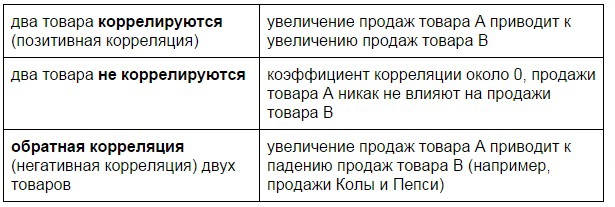
最初に、売上の相関関係を扱います。 商品の売上が店舗の総売上高と他のカテゴリの売上にどのように影響するか。 3つの可能なシナリオがあります。
ほぼすべての店が大量の牛乳を販売していることがわかっています。 牛乳の売り上げと店舗の売上高は直接相関しているという仮説を受け入れます。 牛乳販売データを青で、売上高データを赤で示します。
plotPair <- function(x,y,namesX,namesY){ par(mfrow=c(2,1)) plot(x,type='l',col='red',main=namesX,xlab='') plot(y,type='l',col='blue',main=namesY,xlab='') par(mfrow = c(3,2), oma = c(5,4,0,0) + 1, mar = c(0,0,1,1) + 1 ) layout(matrix(c(1,2,3,4,5,5), 3,2, byrow = TRUE)) plot(x,type='l',col='blue',ylab='log sales qty',main=namesX,xlab='') plot(y,type='l',col='red',main=namesY,xlab='') hist(x,col='blue',main=names(x),breaks=20) hist(y,col='red',main=names(y),breaks=20) m<-lm(y~x) plot(x,y,xlab=namesX,ylab=namesY) abline(m,col='green',lwd=3) } plotPair(x=moloko_df$...', y=moloko_df$sum, namesX='...', namesY='')
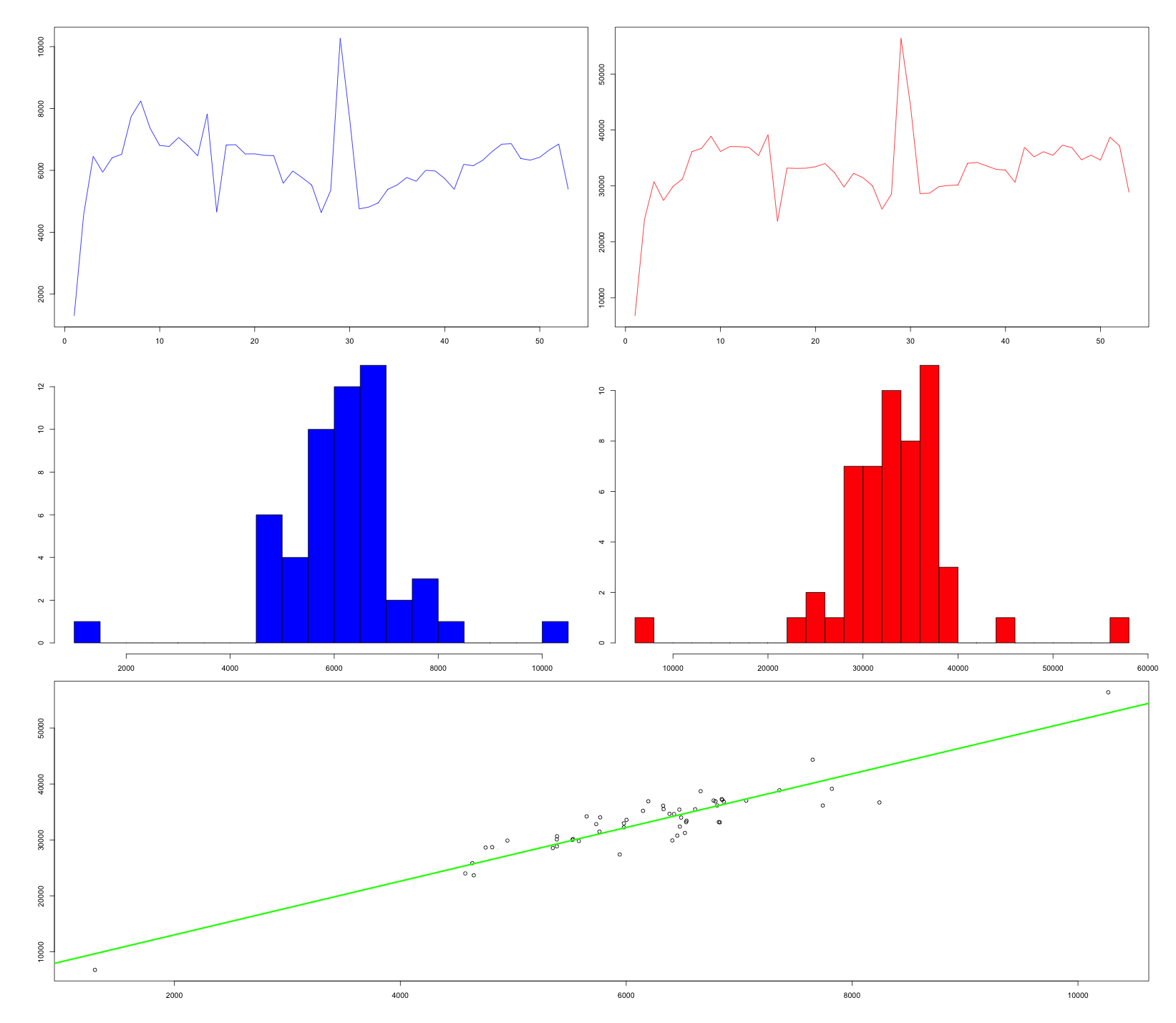
図に見られるように、左と右のグラフィックを比較すると、それらはほとんど同じです。
下の図では、「牛乳と乳製品」を水平に、「反転」を垂直に表示しましたが、ここでも線形の関係を確認できます。 したがって、我々の仮説は真実でした。
顧客は牛乳を求めて店に来ますが、他の商品も購入します。つまり、乳製品の価格を下げても店が顧客を引き付けることは有益です。
しかし、今、私たちは質問、相関の対象となるすべての商品を見つける方法、および商品の売上が店舗の売上高とどのように相関するのかに興味を持っています。 相関行列を使用します。
corr<-function(df){ cr <-cor(df, use="complete.obs") par(cex = 0.9) corrplot.mixed(corr=cr,upper="ellipse", tl.pos="lt", col = colorpanel(50, "red", "gray60", "blue4"), cl.cex=0.5,tl.cex=1.1) }
食料品販売の相関

*マトリックスを構築する場合、ゼロに近い相関は円とグレーで示され(当社が選択した色域を使用)、ゼロからの振動の大きさは楕円とその色によって決定されます:正の相関の場合は青、負の場合は赤
マトリックスに基づいて、売上が店舗の売上高と相関する上位製品を強調表示できます
パンとパン屋さん0.977
非食品0.950
牛乳および乳製品0.934
ソーセージ0.930
スナック0.870
たばこ製品0.835
菓子0.802
糖尿病栄養0.794
食料品0.782
私たちの経験では、パン、バッグ(非食品)、ミルク、ソーセージは、世界中のほぼすべての店舗で高い相関係数を持っています。 店に来る人は通常、これらの製品を1つ以上購入します。 ただし、この特定のケースでは、スナック、タバコ、菓子製品が異なります。つまり、デリには、これらの商品グループ専用に来店する顧客がいます。
ここで、レシート内の商品への参照頻度の分析を適用します。これは、製品ではなく顧客指向のアプローチです。
デリによると、領収書での商品の言及の頻度の相関
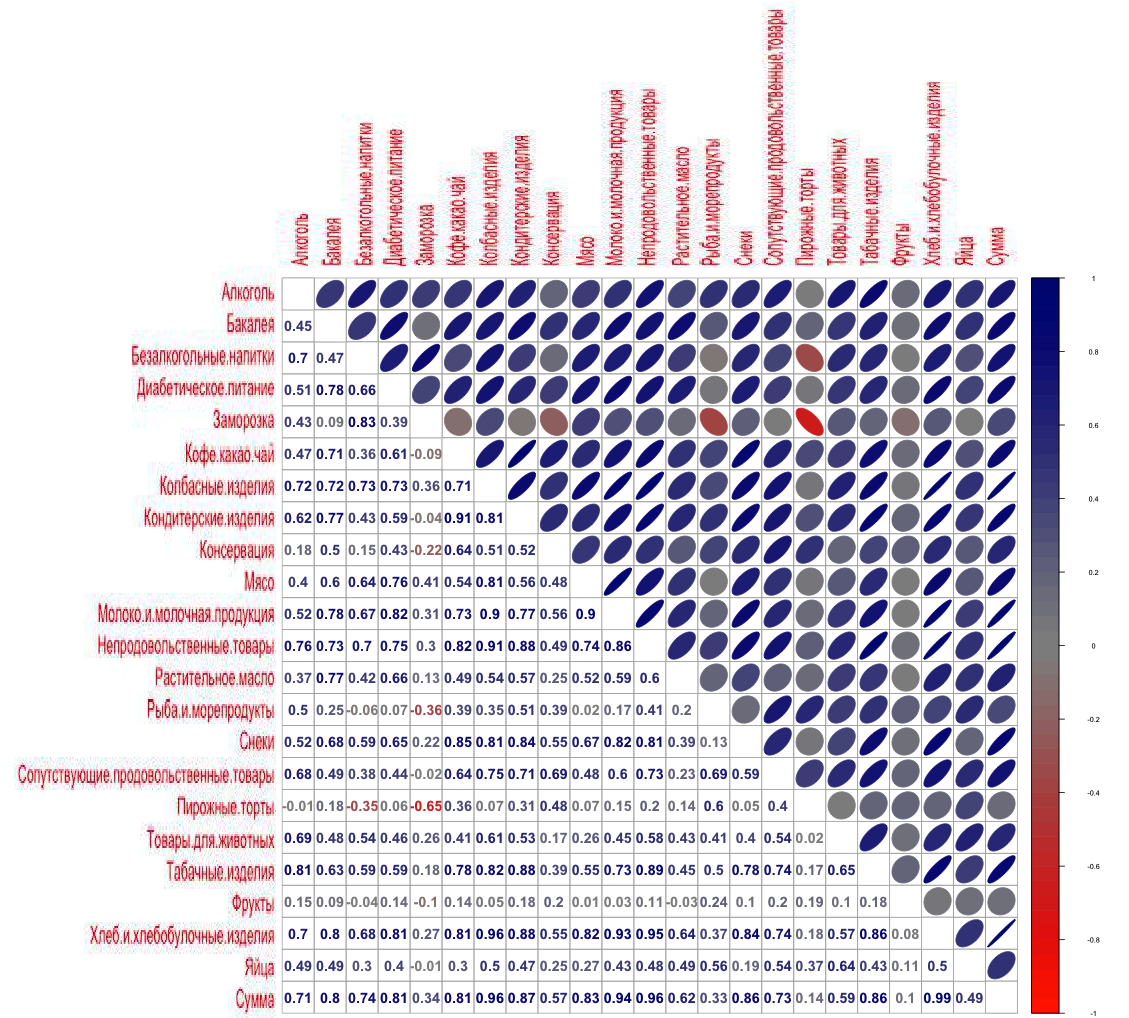
このマトリックスから、領収書の商品への参照の頻度の高さを特定します。
パンおよびパン製品0.986
ソーセージ0.961
非食品製品0.956
ミルク。 および乳製品0.944
菓子類0.867
スナック0.864
たばこ製品0.858
肉0.829
糖尿病栄養0.812
ご覧のとおり、上位のカテゴリとカテゴリ別の数値でさえほぼ同じままです。
2番目のストアにも同じアプローチを適用します。
スーパーマーケットの販売相関
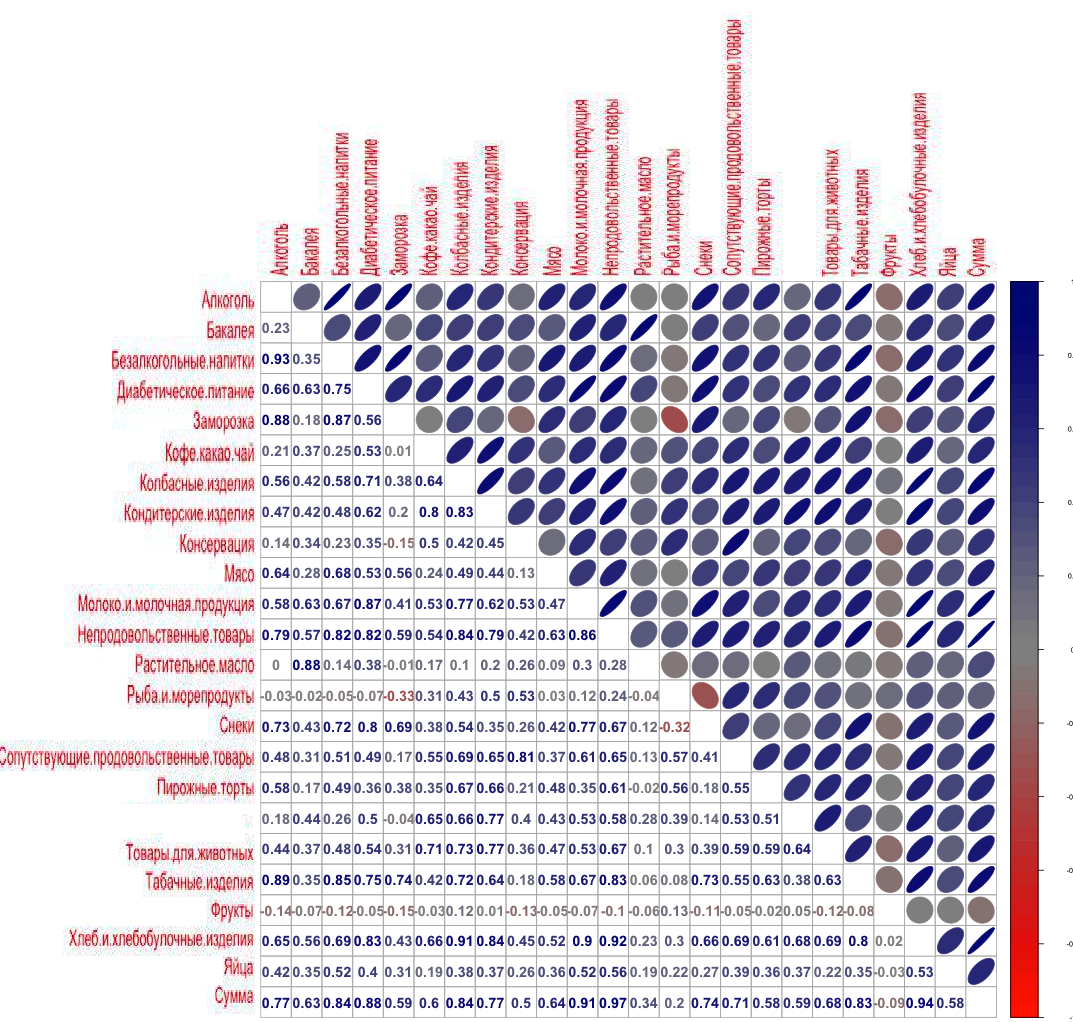
そして、ここですでにデリとの大きな違いが見られます。
スーパーマーケットマトリックスは、別のトップセラー製品を示しています。
非食品製品0.966
パンとパン屋さん0.943
牛乳および乳製品0.908
糖尿病栄養0.882
ソーセージ0.840
ソフトドリンク0.837
たばこ製品0.835
菓子0.775
アルコール0.773
スーパーマーケット全体の小切手での商品への参照の頻度の相関

スーパーマーケット全体の小切手における商品への参照の頻度:
非食品0.975
パンとパン屋さん0.968
牛乳および乳製品0.948
ソーセージ0.927
糖尿病栄養0.905
菓子0.899
たばこ製品0.858
ソフトドリンク0.819
アルコール0.785
ご覧のとおり、スーパーマーケットでは、デリの食料品やスナックの代わりに、ノンアルコール飲料とアルコールの2つの新しいカテゴリがトップになりました。
おそらく、店舗の場所と競争環境に依存します。
相関行列は、分析の大きな機会を与えてくれます。
これらのマトリックスを分析するときに焦点を当てたいのは、相関(正または負)、非相関製品だけでなく、分析する価値があることです。 たとえば、植物油は商品の他のカテゴリや店舗の一般的な売上高とは相関しません。 同様に、小切手の分析では、植物油だけを求めて来店するバイヤーがいることが示されています。 したがって、マーケターはそれをどこでもトレーディングフロアに置くことができ、買い手は必要な商品を見つけることができます。
別の側面として、魚やスナックなど、一部の製品には逆相関があります。 これは、人々が原則として、好みに応じてビール+スナックまたはビール+魚のいずれかを摂取するという事実によって簡単に説明されます。 魚とスナックの両方を同時に買う人はほとんどいません。 状況は、アイスクリームと新鮮な魚、アイスクリーム、ケーキでも同様です。
商品間のリンクの詳細な分析は、役に立つかもしれない多くのそのような事実を与えます。
相関分析は、現在の状況を示しており、製品は店舗の売上に大きく影響しています。 しかし、どれが最も重要ですか? これは、次の記事で取り上げる線形モデルの使用を検討する方が簡単です。