
まず、調査方法について簡単に説明します。 適切な調査の特徴の1つは、サンプルの代表性です。 母集団から同じ確率で無作為に選択された回答者が、返品なしで単純な無作為標本を決定します。 いくつかの理由により、代表的な単純なランダムサンプルを取得することは非常に困難です。 通常、代表性のために、人口は層に分割され、調査のコストを削減するために、各層にクラスターが割り当てられます。 さらに、人口の既知の指標(性別、年齢グループなど)の公平な推定値を取得するために、研究に参加した回答者には重みが割り当てられます。 詳細は、A。Churikov [1]の記事に記載されています。
層化、クラスタリング、および重み付けを使用したサンプリングは、もはや単なるランダムではありません。 そのようなサンプルの変数については、古典的な統計検定で必要なiidの原則に違反しています。 特に、サンプルのクラスタリングは、観測値のクラス内相関により、結果の統計誤差を増加させます。
「通常の」式との違いの別の例は、サンプル平均の分散を見つけることです。 xを重みwの数値または論理ポーリング変数とします。 それから
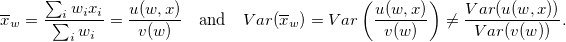
したがって、関数u / vの比は、テイラー級数(1次項への展開に制限されます)を使用してラナー化され、この級数の各メンバーに対して分散が求められます。 サンプル平均の分散を推定するこの方法は1つだけではなく、他の方法もあります。 詳細、式、および例については、第3章の書籍[2]を参照してください。
幸いなことに、Rには調査パッケージがあり、回答者の調査によって得られたデータの統計分析を実行できます。 このパッケージの作者T. Lumleyは、本の形で出版された詳細なユーザーマニュアルを書きました[3]。 他のソフトウェア(SAS、Stata、SUDAAN)で調査の結果を扱った人のために、記事が利用可能です[4]。 さらに、本[2]のサポートページでは 、この出版物のほとんどの例について、コードがいくつかのプログラミング言語、特にRで出版されています。
各国のESSデータには、層別化(stratify)、クラスター(psu-主要サンプル単位)、および回答者の確率(prob)に関する情報があります。 通常、重みは確率に反比例します。 そのため、ロシアの場合、地層は連邦地区であり、クラスターはこれらの地区の多くの都市および地域です。 ESSの調査設計の詳細と例は、プロジェクトのWebサイトから取得したこのpdfで提供されます。
問題の声明。
記事の前の部分で、見つかったルールの1つについて、次の結果が得られました。

ここで、前件-ルールX-> Yの左側の部分は、回答者が
-田舎のほとんどの居住者にとって、生活はすぐに悪化するという声明に完全に同意する
そして
-金持ちであること、大金、高価なものを持っていることが重要な人で自分を擬人化しないでください。
3か国すべてでXのシェアの信頼区間を見つけ、フランスのサポートXの結果がデンマークおよびロシアのサポートXとは大きく異なることを示す必要があります。
データ準備。
ESS 6ウェーブデータ(バージョン2.1)と調査設計情報をRにロードします。
データは公開されていますが、ダウンロードするには登録が必要です。 承認後、ここから stataデータを作業ディレクトリRにダウンロードします。
# デンマークの調査設計データ
# フランスの調査設計データ
# ロシアの調査設計データ
library(foreign) # to read data library(data.table) # to manipulate data srv.data <- read.dta("ESS6e02_1.dta") srv.variables <- data.table(name = names(srv.data), title = attr(srv.data, "var.labels")) srv.data <- data.table(srv.data) setkey(srv.data, cntry) setkey(srv.variables, name)
# デンマークの調査設計データ
dk.dt <- data.table(read.dta("ESS6_DK_SDDF.dta")) dk.dt <- dk.dt[cntry!="NA",] # sic! this base contains extra records with NA data dk.dt[,stratify:="dk"] # dk sample is simple random sample dk.dt[,psu:=seq(3300,length.out = nrow(dk.dt))] #to avoid duplication with psu numbers of the fr data
# フランスの調査設計データ
fr.dt <- data.table(read.dta("ESS6_FR_SDDF.dta"))
# ロシアの調査設計データ
ru.dt <- data.table(read.dta("ESS6_RU_SDDF.dta"))
必要なデータベースを作成し、それにステートメントXをサポートする変数を追加します
countries.set <- c("FR", "DK", "RU") cntries.srv.data <- srv.data[J(countries.set)] setkey(cntries.srv.data, cntry, idno) # idno is unique respondent's ID inside cntry cntries.dt <- rbind(dk.dt, fr.dt, ru.dt) setkey(cntries.dt, cntry,idno) cntries.srv.data <- cntries.srv.data[cntries.dt] # merge the databases cntries.srv.data[,weight:=dweight*pweight] # weight is defined as design weight adjusted on the countries population sizes # add antecedent (denoted as lhs) statement to the cntries.srv.data lhs.rule.adding<-function(lhs){ statements <- unlist(strsplit(lhs, " & ")) statements <- lapply(statements, function(l) unlist(strsplit(l,"="))) statements <- lapply( statements, function(l) c(question.name=srv.variables[title==l[1], name], answer=l[2]) ) conditions <- sapply( statements, function(l) paste("ifelse(is.na(", l[1], "), 0, ", l[1], " == '", l[2], "')", sep="") ) conditions <- paste(conditions, collapse = " & ") add.lhs.to.base <- paste("cntries.srv.data[,x:=", conditions,"]",sep="") eval(parse(text=add.lhs.to.base)) cntries.srv.data[,x:=as.numeric(x)] return(T) } lhs.rule.adding("For most people in country life is getting worse=Agree strongly & Important to be rich, have money and expensive things=Not like me") cntries.srv.data[,cntry:=factor(cntry, levels = countries.set)]
結果のベースでは、研究デザインを設定します
library(survey) design.cntries.data <- svydesign(ids = ~psu, strata = ~stratify, weights = ~weight, data = cntries.srv.data)
問題の解決策。
調査パッケージのsvymean()関数は、調査の設計を考慮して、サンプルの平均値だけでなく、特にその標準偏差を見つけます。 次に、各国のサポートXに個別に等しい分数pの信頼区間は、次のように見つけることができます。
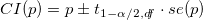 。
。
信頼区間を見つけてプロットするためのRコード
X.supp.confint <- sapply(countries.set, function(country) { design.dt<-subset(design.cntries.data, cntry==country) w.mean<-svymean(~x, design.dt) c(w.mean[1],confint(w.mean,df = degf(design.dt))[1,]) }) X.supp.confint <- data.table(t(X.supp.confint)*100, country=c("France", "Denmark", "Russia")) setnames(X.supp.confint, 1:3, c("mean","lower","upper")) library(ggplot2) limits <- aes(xmax = upper, xmin=lower) p <- ggplot(X.supp.confint, aes(y=country, x=mean, colour=country)) + geom_point(size=4, shape=18) + geom_errorbarh(limits, width=0.2, lwd=1.0) p <- p + ggtitle("95 % confidence intervals for the antecedent proprotions") + xlab("Percentage of population") p + theme_bw() + theme(plot.title=element_text( face="bold", size=16), axis.text.y = element_text( face="bold", size=14), axis.text.x = element_text( face="bold", size=14), axis.title.x=element_text( face="bold", size=14), axis.title.y=element_blank(), legend.position="none")
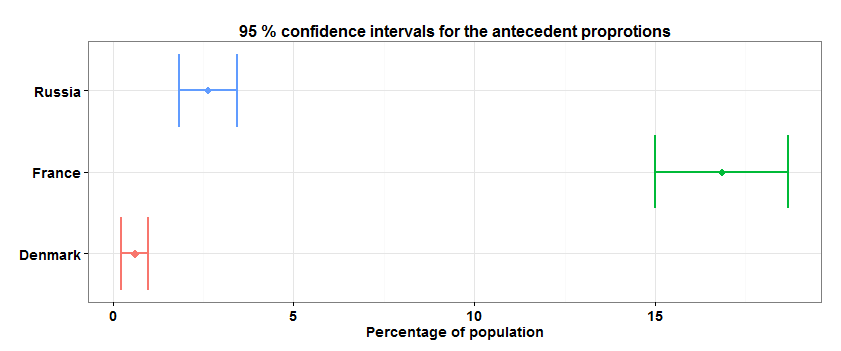
調査パッケージでは、株式の信頼区間を推定するための二項法も利用可能であることを追加します-svyciprop()関数。
検討中の国におけるサポートシェアXの違いの重要性を確認するために、次の形式のロジスティック回帰を構築します。
model <- svyglm(x~ cntry, design = design.cntries.data, family=quasibinomial)
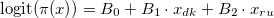
この線形モデルの係数は、「通常の」ロジスティック回帰とまったく同じ意味です。 それは
sapply(c(coef(model)[1], sum(coef(model)[c(1,2)]), sum(coef(model)[c(1,3)])), function(b) exp(b)/(1+exp(b)))*100
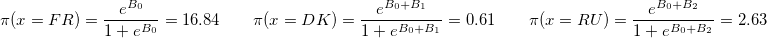
このモデルの結果は、係数B_1とB_2がゼロとは大きく異なることを示しています。 つまり、フランスのサポートXのシェアは、デンマークとロシアの対応するシェアと統計的に有意に異なります。
library(DT); datatable(round(coef(summary(model)),4))

最後に、両方のモデル係数-B_1とB_2が同時にゼロであるという帰無仮説を棄却します
regTermTest(model, ~cntry, method = "LRT")
Working (Rao-Scott+F) LRT for cntry in svyglm(formula = x ~ cntry, design = design.cntries.data, family = quasibinomial) Working 2logLR = 379.0228 p= < 2.22e-16 (scale factors: 1.2 0.8 ); denominator df= 2088
考慮される3カ国のサポートXの値は非常に異なるため、調査の設計情報を使用せずにロジスティック回帰係数の帰無仮説を拒否することができます。 私は、調査の設計データを使用するかどうかに応じて、一定のレベルのエラーで仮説が受け入れられるか拒否されるかの例を示すことを目指していませんでした。
ただし、そのような状況は可能性があります。 本[2]の例6.8を検討してください。NCS-Rデータを使用して、若い成人(18〜28歳)のアルコール依存と教育レベルの独立性をテストします。 。
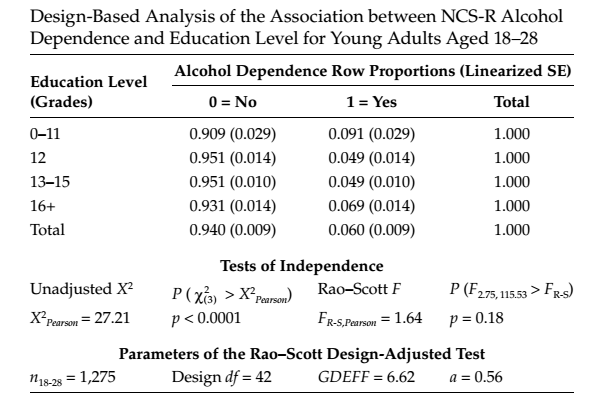
この例では、18〜28歳の米国市民における「アルコール依存と診断された」変数と「教育レベル」の変数の独立性に関する帰無仮説をテストします。 標準の基準X ^ 2は、1%未満のエラー確率でこの仮説を棄却します。つまり、指定された母集団内のこれらの変数間に関係があると自信を持って言えます。 一方、研究の設計のためにRao-Scottによって修正されたカイ2乗検定は、帰無仮説の誤差を10%以上決定します。 5%レベルで帰無仮説を拒否することはすでに不可能であることがわかります。
したがって、一般的な場合、調査の結果の統計分析は、研究の設計を考慮して実行することが好ましい。
結論として、最近、国際的な結果の分析のために、構造方程式を使用したモデリングが使用されていることに注意します。 この理由の1つは、サンプルの層別化とクラスタリングが通常、一般集団ではなく国レベルで行われることです(これはESSの場合とまったく同じです)。 しかし、これについてはしばらくしてから、記事のコレクションについて言及しています[5]。
参照:
[1] Churikov A.社会学的研究におけるランダムおよび非ランダムサンプル、g。 社会的現実、4、2007、pp。89-109。
[2] Heeringa SG、ウェストBT、バーグランドPA応用調査データ分析、CRCプレス、2010年。
[3] Lumley T. Complex Surveys:A Guide to Analysis Using R、Wiley、2010。
[4] Damico A. Rへの移行:健康政策データにおけるSAS、Stata、およびSUDAAN分析手法の複製、R Journal Vol。 2009年12月1/2日。
[5]異文化分析:メソッドとアプリケーション(Davidov E.、Schmidt P.、Billiet J.編)、Routledge、2011年。