Wolfram言語でのドロステ効果の作成（Mathematica）

John MacLoonの投稿「 Droste Effect with Mathematica 」の翻訳。 記事のコードは、投稿の最後にダウンロードできます。

翻訳に協力してくれたキリル・グゼンコに深く感謝します。

---

ドロステ効果（ wiki ）は、画像を再帰的に含めることです。 この名前は、1904年に看護師が入った箱を持った看護師などを描いたパッケージで販売されたドロステココアパウダーに由来しています。 最も簡単な実装は、画像を拡大縮小して変換し、変更されていない正確なコピーに配置してから、プロセスを再開することです。 オリジナルのDrosteパッケージイラストを使用したデモをご覧ください。 ただし、複素変数（TFKP）の関数の理論を使用することで、さらに興味深い結果を得ることができます。 Escher M.K.は、画像に適用されるコンフォーマルマッピングのアイデアを最初に普及させましたが、コンピューターの助けを借りて、このアイデアを写真で簡単に実現して、次のようなものを得ることができます：







はい、アイデアは新しいものではありません。 しかし、同様の効果を実装することを決めたとき、ネットワーク上で見つけた方法は私には不十分なようでした。 一部の人は、画像に対して多くのコピー＆ペーストタイプの作業を提案しましたが、他の人は、画像の一部の接合部で解像度の不一致の問題を抱えていました。 そして、いつものように、ここではMathematicaを使用する必要があるという結論に至りました。この場合はgrid Mathematicaです。



本質的に、アイデアはシンプルです。 結果の画像の位置{ x、y }のピクセルが元の画像の位置f [{ x、y }]のピクセルから取得される画像を作成します。 魔法は、関数f自体を選択することです。 しかし、これに到達する前に、何かを準備する必要があります。



現在、 Mathematicaには画像の任意の変換のための操作が含まれていないため、最初にそれらを実装する必要があります（ PostはJohnによってWolfram Mathematicaの第7バージョンで記述され、第8バージョンではこれらの目的のために特別なImageTransformation関数が登場し、コードの量を大幅に削減しますジョンの記事で-Ed。 ）。 重要なポイントは、ピクセル間の色を絶えず計算して、画像の拡大領域での解像度マッチングの問題や不必要なピクセル化を防ぐことです。 私の方法は、画像の各RGBチャンネルのピクセルのすべての色を線形補間することです。 これは、特に10メガピクセルの元の画像で最も計算が複雑なアプローチですが、必要な品質が得られます。







このアプローチを補うために、すべてを並列コンピューティング用に設定しました。 はじめに、 Mathematicaに組み込まれている並列化ツールを使用しました 。 したがって、 Tableを使用してピクセルのグリッドを生成する代わりに、 Tableを呼び出して最終画像のレイヤーを生成する関数を作成しました。これは、 ParallelTableによって並列に呼び出され、複数のプロセッサコア間で作業を再分散します。 したがって、3〜4行多くなりますが、これは並列化の作業の半分に過ぎません。











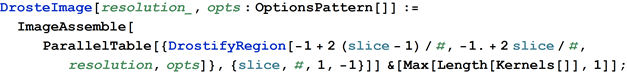
次に、元の画像を各プロセッサに渡し、補間関数を設定します。 この部分は計算が非常に難しいため、これを一度だけ行い、その後、この仕事を再度行うことなく、ソースからあらゆる種類の画像を作成できるようにします。 ここでは、並列化は非常に簡単です。利用可能なカーネルが起動され、プログラム定義がすべてのカーネルに配布され、 ParallelEvaluate関数を使用して、補間関数を作成する要求のあるリンクを介してイメージを送信します。







実際の非圧縮データを送信するのではなく、JPGファイルの内容を含む文字列として画像を送信する方法には、優雅な手法があります。 はるかに小さいオブジェクトが判明するため、より高速に送信されます。



この設定により、グリッドMathematicaを使用して計算を高速化するために、オフィスから追加のコンピューターコアを簡単に引き付けることができます。



コードに追加するものが他にあります。 そのため、元の画像を正しい比率で正しいセンタリングでトリミングする必要性を取り除きます。







トリミング後の元の画像は次のとおりです。







さて、すべてが退屈している、今が楽しい時です。



私が使用するねじれは、複素平面上のPower関数の特定のプロパティに基づいています。 座標ペア{ x、y }を複素数p = x + I yの一部として表すことができ、マップf [ p ]：= p ^cを使用してデカルト座標に戻ります。 特に、より一般的なモデルa +（ b + c p ） ^dを使用する場合、{ a、b、c、d }が複素数である場合、 cの値を取得する方法を理解することは非常に困難です。 そこで、Wolfram Demonstrations Projectに目を向け、そこでコンフォーマルマッピングのデモを見つけ、興味のあるマッピングを得るためにコードを少し変更しました。



実験して、パラメーターの影響を見つけ、キャリブレーションを設定し、適切な初期値を取得し、魔法の数式の必要な場所に名前付きオプションを設定しました。 最終的に、私はそのようなねじれのデザインを得ました。







画像の外側のピクセルにアクセスしようとすると内側にジャンプし、特定の領域内のピクセルにアクセスしながら外側にジャンプすることで、この種の自己複製を提供します。



美観上の理由から、画像間のつながりを閉じてより自然にしたいと思います。 私の例では、額縁を使用しましたが、出入口、窓、コンピューターのモニターなどが使用されている例に会いました。



このプロセスの自動化により、手動でのコピーとその後の貼り付けが回避され、画像のさまざまな部分の解像度の不一致に関する問題も回避されます。







すべて、すべての骨の折れる仕事はすでに遅れています、今がふける時間です。 内部領域の座標を設定して、元の画像でカーネルを初期化します（ 2D描画パレットの座標ピッカーを使用して簡単に取得できます）。







次に、高さ400ピクセルの画像を生成します。







二重らせんを使用したこのようなオプションの多くの組み合わせがあります。







反対方向の1つのスパイラル：







スパイラルがなければ、複製のみ：







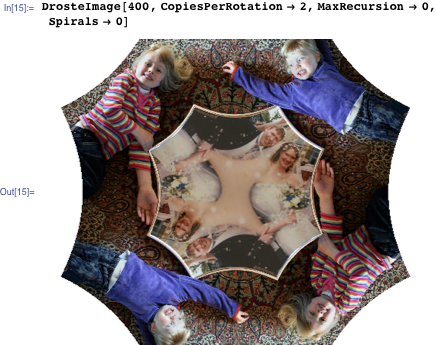
このコードは、スパイラルごとに2つのコピーを作成することにより、八角形を作成します。







そして、これは再帰とスパイラルなし-一緒にロールされた2つのコピーのみ：







そしてここで、クライマックスはDVD品質の映画全体であり、画像を再帰的ならせん状にねじるドロステ効果を示しています。







このようなビデオを作成するには、多くの計算が必要です。60個のフレームごとに、約1,000万回、1000万ピクセルごとに3つの補間関数を呼び出す必要があります。 これは、私の並列化の努力が実を結ぶ瞬間です。 もちろん、Wolfram Researchでは、 Wolfram Lightweight Grid Managerから複数のグリッドMathematicaライセンスを利用できます（ Wolfram Mathematicaバージョン7以降、並列化機能はWolfram Languageコアに含まれており、作業時に追加のプログラムを必要としませんが、コンピューターで利用可能なすべてのカーネルを使用できますが、クラスターに接続する必要がある場合は、gridMathematicaが必要です-約 Parallel Configurationの設定を開くと、すべてが魔法のように表示されます。 数回クリックするだけで、小さなラップトップの2つに加えて16個のコアが追加され、コードを変更しなくても、ムービーは8倍速くなります（並列化しない場合より16倍速くなります）。 このコードがどこで機能するのか正確にはわかりませんが、プログラムとソース画像は自動的に転送されるため、あまり面白くありません。 これがどのように設定されているかを示す画面デモを見ることができます。







このコードはさまざまな方法で変更できます。 たとえば、 ReplicateRegionを変更すると、たとえば、非長方形のフレームを円の形で使用したり、 複製の色や透明度を変更することもできます。 あなた自身で実験してみて、それから何ができるかを見てください。