はじめに
フィボナッチ数のプログラマーはもううんざりしているはずです。 それらの計算の例はどこでも使用されます。 これらはすべて、これらの数値が再帰の最も単純な例を提供するという事実に帰着します。 動的プログラミングの良い例でもあります。 しかし、実際のプロジェクトでこのように計算する必要がありますか? 必要ありません。 再帰も動的プログラミングも理想的なオプションではありません。 そして、浮動小数点数を使用する閉じた式ではありません。 それでは、正しく行う方法を説明します。 しかし、最初に、すべての既知のソリューションを見ていきましょう。
コードはPython 3向けですが、Python 2向けにもなるはずです。
はじめに-定義を思い出します:
F n = F n-1 + F n-2
およびF 1 = F 2 = 1。
閉じた式
詳細は省略しますが、希望する人は式の結論に慣れることができます。 F n = x nである特定のxがあると仮定して、xを見つけます。
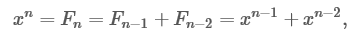
つまり
カットx n-2
二次方程式を解きます:
これは、「ゴールデンセクション」が成長する場所ですϕ =(1 +√5)/ 2。 初期値を代入して別の計算を行うと、次のようになります。
F nの計算に使用します。
from __future__ import division import math def fib(n): SQRT5 = math.sqrt(5) PHI = (SQRT5 + 1) / 2 return int(PHI ** n / SQRT5 + 0.5)
良い:
小さいnで高速かつ簡単
悪い点:
浮動小数点演算が必要です。 nが大きい場合、より高い精度が必要です。
悪:
複素数を使用してF nを計算することは 、数学的な観点からは美しいですが 、コンピューターにとってはいものです。
再帰
すでに何度も見た最も明白な解決策は、再帰とは何かの例として最も可能性が高いです。 完全を期すために、もう一度繰り返します。 Pythonでは、1行で記述できます。
fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1
良い:
数学的な定義を繰り返す非常にシンプルな実装
悪い点:
指数リードタイム。 nが大きい場合、非常に遅い
悪:
スタックオーバーフロー
暗記
再帰的な解決策には大きな問題があります:計算の交差。 fib(n)が呼び出されると、fib(n-1)とfib(n-2)がカウントされます。 ただし、fib(n-1)がカウントされると、fib(n-2)が独立してカウントされます。つまり、fib(n-2)は2回カウントされます。 議論を続けると、fib(n-3)が3回カウントされることがわかります。 交差点が多すぎます。
したがって、結果を再度カウントしないように、結果を覚えておく必要があります。 このソリューションは、時間とメモリを直線的に消費します。 ソリューションでは辞書を使用していますが、単純な配列を使用できます。
M = {0: 0, 1: 1} def fib(n): if n in M: return M[n] M[n] = fib(n - 1) + fib(n - 2) return M[n]
(Pythonでは、これはデコレータfunctools.lru_cacheを使用して行うこともできます。)
良い:
再帰を記憶されたソリューションに変えてください。 指数関数的な実行時間を線形に変換します。これにより、より多くのメモリが消費されます。
悪い点:
多くのメモリを消費します
悪:
再帰のようなスタックオーバーフローが可能
動的プログラミング
暗記による決定の後、以前のすべての結果ではなく、最後の2つだけが必要であることが明らかになりました。 さらに、fib(n)で開始して戻る代わりに、fib(0)で開始して先に進むことができます。 次のコードの実行時間は線形であり、メモリ使用量は修正されています。 実際には、再帰的な関数呼び出しとそれに関連する作業がないため、ソリューションの速度はさらに高くなります。 そして、コードはよりシンプルに見えます。
このソリューションは、動的プログラミングの例としてよく引用されます。
def fib(n): a = 0 b = 1 for __ in range(n): a, b = b, a + b return a
良い:
小さいnの単純なコードで高速
悪い点:
まだ線形ランタイム
悪:
はい、特別なことはありません。
行列代数
そして最後に、時間とメモリの両方を適切に使用して、最も明るくなく、最も正確なソリューションを実現します。 同種の線形シーケンスに拡張することもできます。 マトリックスを使用するという考え。 それを見て
これを一般化すると、
先に取得したxの2つの値のうち、そのうちの1つはゴールデンセクションであり、行列の固有値です。 したがって、閉じた式を導出する別の方法は、行列方程式と線形代数を使用することです。
それでは、この定式化はどれほど有用ですか? べき乗は対数時間で行えるという事実。 これは二乗することで行われます。 一番下の行は
最初の式は偶数Aに使用され、2番目の式は奇数に使用されます。 行列の乗算を整理するためだけに残り、これで完了です。 次のコードが判明します。 理解しやすいように、powの再帰的な実装を編成しました。 ここで反復バージョンを参照してください。
def pow(x, n, I, mult): """ x n. , I – , mult, n – """ if n == 0: return I elif n == 1: return x else: y = pow(x, n // 2, I, mult) y = mult(y, y) if n % 2: y = mult(x, y) return y def identity_matrix(n): """ n n""" r = list(range(n)) return [[1 if i == j else 0 for i in r] for j in r] def matrix_multiply(A, B): BT = list(zip(*B)) return [[sum(a * b for a, b in zip(row_a, col_b)) for col_b in BT] for row_a in A] def fib(n): F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply) return F[0][1]
良い:
固定メモリ、対数時間
悪い点:
より複雑なコード
悪:
マトリックスを扱う必要がありますが、それほど悪くはありません
性能比較
動的プログラミングのオプションとマトリックスのみを比較する価値があります。 それらを数字nの文字数で比較すると、行列解は線形であり、動的計画法による解は指数関数的であることがわかります。 実用的な例は、fib(10 ** 6)、つまり20万文字を超える数を計算することです。
n = 10 ** 6
fib_matrixを計算します。fib(n)の合計は208988桁で、計算には0.24993秒かかりました。
fib_dynamicを計算します:fib(n)の合計は208988桁で、計算には11.83377秒かかりました。
理論的発言
上記のコードに直接触れないで、このコメントにはまだ興味があります。 次のグラフを検討してください。
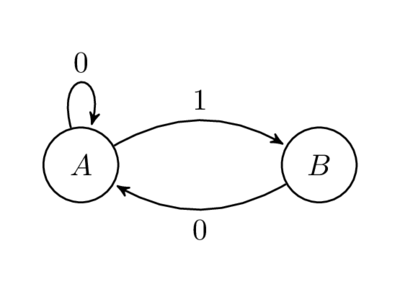
長さnのパスの数をAからBまで数えます。たとえば、n = 1の場合、1つのパスがあります。n= 2の場合、1つのパス01があります。n= 3の場合、2つのパス001と101がありますAからBまでの長さnのパスの数が正確にF nであることを示すのは非常に簡単です。 グラフの隣接行列を作成すると、上で説明したものと同じ行列が得られます。 これは、与えられた隣接行列Aについて、A nの出現がグラフの長さnのパスの数であるというグラフ理論からのよく知られた結果です(映画Good Will Huntingで言及されている問題の1つ )。
端にそのような兆候があるのはなぜですか? 両側が無限であるグラフ上の一連のパス上で無限の文字シーケンスを見ると、「 サブタイプの有限タイプ 」と呼ばれるものが得られることがわかります。これは、記号ダイナミクスのシステムの一種です。 特に、この有限タイプのサブシフトは「ゴールデンセクションのシフト」として知られており、「禁止語」のセットで定義されます{11}。 言い換えれば、両方向に無限であり、それらのペアが隣接していないバイナリシーケンスを取得します。 この動的システムのトポロジカルエントロピーは、黄金比equalに等しくなります。 この数が数学のさまざまな分野でどのように定期的に現れるかは興味深いです。