 約1年前、友人が私に行って、それがどのようにプレイされるかを示しました。 最初のゲームの1つで、ボードの下側を上に接続する石のチェーンと、左側を右に接続するチェーンを誇らしげに構築したことをよく覚えています。友人がこれを確かに良いと教えてくれましたが、私は失いました。 その後、その理由を理解するのに長い時間がかかりました。 それ以来、私は最初のKGS段について進み、友人は私と遊ぶのをやめました。
約1年前、友人が私に行って、それがどのようにプレイされるかを示しました。 最初のゲームの1つで、ボードの下側を上に接続する石のチェーンと、左側を右に接続するチェーンを誇らしげに構築したことをよく覚えています。友人がこれを確かに良いと教えてくれましたが、私は失いました。 その後、その理由を理解するのに長い時間がかかりました。 それ以来、私は最初のKGS段について進み、友人は私と遊ぶのをやめました。
外出先でうまくプレイするには、いくつかの動きを先に見る必要があります。このスキルは、多くの問題を抱えている解決策をうまく開発します。 当然のことながら、ある日、これらの事柄の格子を書いて、理想的には問題に埋め込むのがいいだろうという考えに打たれました。特に、adumがこの考えを承認するので。 私自身は、数秒で約1の速度で多かれ少なかれ意味のある動きを試行する非常にゆるやかな方法でそれを解決しているので、検索の開始方法を定期的に忘れています(そしてこれは、与えられた問題3を自信を持って解決するのに十分です)。速度と精度は最も単純な検索、つまりdfsで機能し、タスクの複雑さを「数日間」と評価しました。 すぐに、私はこの格子を最も単純なdfsを使って「正面から」素早く書き込もうとしましたが、ちょっとした迷惑につまずきました。 考え直さずに、私は既に決められた位置を保存するためのキャッシュを開始し、すぐに別の迷惑につまずきました:別の動きのシーケンスでこの位置に来ると、一度見つかった解決策は間違っているかもしれません。 ここで私は何をすべきかわからずにハングアップしましたが、このトラブルは簡単に解決できると判断しました。少し考えてみるだけです。 私は長い間考え、このトピックの準備ができているもの、記事、アルゴリズムなどを見ることが理にかなっていると判断しました。 私が最初に出会ったのは、特定の「ラムダ深さ第一証明番号検索」であり、記事のサイズが数ページしかないことを見て、喜んで読み始めました。 この記事には、MartinMüllerとAkishi Kishimotoによる他の同様の記事へのリンクがあり、それらの記事にはリンクもあり、Kishimotoによる200ページの論文へのリンクがあり、問題の規模を認識しました。非常に単純なものでさえ、ほとんどの場合、アルゴリズムの複雑さは非常に複雑でした場合によっては、質問はすべてのオプションをどのようにソートするかではなく、ボード上で何かを見つける方法(初心者でもすぐに何をするか)、何をキャプチャまたは防御する必要があるかを理解する方法(人にとっても些細なこと)、およびどのような動きがありますか これは(ほとんどの場合も明らかです)オプションの実際の列挙に関しては、決定されたと言えます(ただし、効果的な列挙アルゴリズムは非常に注意が必要です)。 一般に、私のIQは明らかに外出先でこのような問題を解決するのに十分ではないことに気付き、すべての意味のある動きと目標が事前に設定されている最も単純なケースのソルバーを少なくとも書ければいいと判断しました-これは問題でも非常に役立ちます。
私の知る限り、すべてを解決するプログラムはほとんどありません。
-Thomas WolfのGoTools:最大15の可能な動き、クローズドソース、非常に高度な静的解析を備えた簡単なdfs。
-Martin MullerのTsumego Explorer(ちなみに7が与えられます):最大30の可能な移動、オープンソースJava(どこで入手できるかは明確ではありませんが)、Mullerの記事と論文で説明されている非常に高度な静的分析による高度なl-df-pn-r検索岸本。
-Martin MullerのFuego:オープンソースのC ++(SourceForgeからダウンロード可能)を使用して、本格的な2+ボットが提供されます(私よりも明らかに強力なので、その強さは評価できません)。
Müllerもadumもjs格子を聞いていません(そして、格子はgosbleblemsに埋め込むことができるようにjs上になければなりません)、もしそうなら、それを書くことは理にかなっています-特にMüllerとKishimotoが多くの記事とこのトピックに関するプログラムですら。
 左は典型的なつめごです。 一般的なケースでは、タスクは黒と白の両方に対して最適な動き(および必要かどうか)を見つけることです。 明らかに、白が先に動いた場合、彼らはコーナーをキャプチャします。 黒が最初に移動すると、角度を保存できますが、解の1つはkoにつながり、黒がkoに負けた場合は角度を失い、もう1つの解はkoなしで角度を保存します。これは通常望ましいことです。
左は典型的なつめごです。 一般的なケースでは、タスクは黒と白の両方に対して最適な動き(および必要かどうか)を見つけることです。 明らかに、白が先に動いた場合、彼らはコーナーをキャプチャします。 黒が最初に移動すると、角度を保存できますが、解の1つはkoにつながり、黒がkoに負けた場合は角度を失い、もう1つの解はkoなしで角度を保存します。これは通常望ましいことです。
簡単にするために、ボードを見て、解決するために整理する必要があるすべての意味のある動きを見つける方法があると仮定します(実際、これはすべての動きが手動で設定されることを意味します)。 ボードbで誰が勝つかを示す関数Rを定義します。
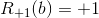 黒が始まり勝った場合。
黒が始まり勝った場合。 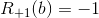 黒が始まり負けた場合。
黒が始まり負けた場合。
Rの定義により、黒は秒のバランスを崩したとしても最初の動きをする義務があります-これは白と黒が絶えず通過する状況を排除します。 白人についても同様です。 黒と白の両方が失われた場合、これらはセクです。 次に、この関数を次のように再帰的に定義できます。
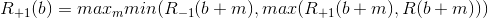
少しわかりにくいですが、その本質はシンプルです。
- Rの定義により、ブラックは何らかの動きを余儀なくされているため、可能な限りすべての動きの中からベストを選択します。 したがって、すべての移動の最大値はmです。
- その後、動きは白になり、彼らは動きをするかしないかを決めるかもしれません-これは最小です。 ホワイトが動きをする場合、結果は
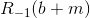 ここで、b + mは、黒い石mが追加されたボードbです。
ここで、b + mは、黒い石mが追加されたボードbです。 - 白が動きを逃した場合(そして、これがRの定義と矛盾しない場合)、黒には選択肢があります:動きをするかセーブするか、ゲームを終了します-これは2番目の最大値です。 黒が動けば、判明
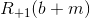 、そして、それらが失敗した場合、R(b + m)は誰が勝ったかを決定します(実際には、これは、捕獲する必要がある石がボード上にあるかどうかを確認するためだけです)。
、そして、それらが失敗した場合、R(b + m)は誰が勝ったかを決定します(実際には、これは、捕獲する必要がある石がボード上にあるかどうかを確認するためだけです)。
白について対称式が得られます。 「額」と数えると、すべてのオプションを列挙した単純なdfsが得られます。これは、5ポイントの最も単純な攻撃でも非常にゆっくりと動作します。 次のように書くことができます。
function solve(board: Board, color: Color): Result { var result = -color; // that's a loss for (const move of board.getMovesFor(color)) { const nextBoard = board.fork().play(move); result = bestFor(color, // it's +color's turn, so he chooses result, bestFor(-color, // now it's -color's turn solve(nextBoard, -color), // -color makes a move bestFor(color, // -color can pass, but then it's +color's turn again solve(nextBoard, color), // +color makes two moves in a row estimate(nextBoard)))); // neither player makes a move } return result; }
このアルゴリズムは、最も単純な秒が秒であることを証明するために多くの時間を浪費することに注意してください。 白と黒のグループに共通の自由のみがあり、これらの自由が多数ある場合、このアルゴリズムは最初に最初の自由でプレイしようとし、それが機能しないことを見つけ、次に2番目の自由でプレイし、再び勝てないことを見つけます。 このアルゴリズムがすべてのオプションを反復するために行う移動の数について、単純な再帰式を作成することもできます。 成長は指数関数以上です。 この問題は、おそらく静的解析によってのみ解決できます。
ここで、同じボードが2回解決されないようにする必要があります。 たとえば、5ポイントの高架道路の解決策を見つけたら、別の位置がその高架道路に下がった場合に再利用できます。 このようなソリューションキャッシュは通常、転置テーブル(tt)と呼ばれます。 このテーブルのキーは、ボードのハッシュ+最初に行く人の色です。 最初は、このように単純に実装しました。
const tt: { [key: string]: Result } = {}; function solve(board: Board, color: Color): Result { const key = color + board.hash(); var result = -color; // that's a loss if (key in tt) return tt[key]; for (const move of board.getMovesFor(color)) { const nextBoard = board.fork().play(move); result = bestFor(color, // it's +color's turn, so he chooses result, bestFor(-color, // now it's -color's turn solve(nextBoard, -color), // -color makes a move bestFor(color, // -color can pass, but then it's +color's turn again solve(nextBoard, color), // +color makes two moves in a row estimate(nextBoard)))); // neither player makes a move } return tt[key] = result; }
この問題の解決策はミュラーと岸本の記事で何度も言及されており、次のように聞こえます:解決策の検索で繰り返しが見つからなかった場合、それは彼らがこの位置に来た方法に依存しません。 あなたがそれについて考える場合、ステートメントはまったく明らかではありません。 私が証明にうんざりしているとき、私はミュラーに手紙を書きました、そして、彼はそうです、これは非常に強くて普遍的な声明であり、証明は論文のどこかにあるようです。 そこにはこの証拠が見つかりませんでしたが、既に解決されたパスに依存しないすべての決定が(メモリ不足のため)削除されることはないと仮定すれば機能する独自の証拠を考えました。
- 13のソリューションは既にキャッシュされており、
- サイクルを検出せずに見つかったすべての中間ソリューションもキャッシュに残りました。
頂点17から始めて、13に到達しようとするとします。証明の本質は、決定ツリーにサイクルがないため、17から13に接続するためにツリーを超える必要があることです。 頂点17は白(まあ、はい、それは赤ですが、それが白であると仮定します)であり、したがって、それからのすべての動きはツリー内にあります。 25番目のブラックピークに達したとしましょう。 頂点は黒であるため、そのソリューション(正しい移動)はキャッシュに書き込まれ(そこからは何も削除されません)、25のソリューションが見つかった後、この仮想パスに沿って進むため、既製のソリューションをキャッシュから取得し、まだツリー内にある白いピークに入ります。 ですから、この仮想的な道をたどり、動きのない行き詰まりに陥るまで待ちます。
ご覧のとおり、ループの問題を解決するには、かなりの量が必要です。
- 位置ではなくパスの解決策を探します:解決(パス:ボード[]、色:色)。
- 検索中に繰り返しに遭遇した場合、それを敗北と見なしますが、同時に、繰り返されるパスの先頭を指します(パスのインデックスを覚えておいてください)。 ペア(結果、インデックス)の意味は、解は無条件ではなく、特定の位置での繰り返しに依存するということです。
- すべての可能な動きの中ですべてが敗北につながる場合、繰り返しを示すすべてのインデックスの中で最小値を見つけ、この最小値を返します。
- 勝ち手がある場合は、可能な限り大きな繰り返しインデックスを持つものを選択することが望ましいです。 最良の場合、ゲインは無条件になります。 パスに依存しません。
これ(および石の自由度を最大化し、他の人の自由度を最小化する単純なヒューリスティック)は、最も単純な大工の正方形を解くのに十分です。
最初の例のように、もっと面白いことを解決するには、coを考慮する必要があります。 考えられるアプローチの1つは、「動的に」検討することです。 検索プロセスで繰り返しが発生する場合は、検索を2つのケースに分岐します(脅威がある場合とない場合)が、このためにはコード全体を徹底的にシャベルする必要があります。 別のアプローチは、次の「静的」な会計です。
- 新しいパラメーターは、外部の脅威の数です。 このパラメーターが+3の場合、黒にはさらに3つの脅威があり、-2の場合、白には2つの脅威があります。
- 決定プロセス中に繰り返しが発生し、この繰り返しに対する脅威がある場合、無駄になり、パスがリセットされます(実際、脅威の目標は、パスをリセットし、ゼロから検索を開始することです)。
- キャッシュ内の決定は、単一の数値(+1または-1)としてではなく、両側の数字の無限の配列として書き込まれ、それぞれの共脅威の数に対して結果が書き込まれます:-2共脅威の場合、白が共脅威を1つだけ持つ場合、白が勝ちます。 secaが判明し、脅威がなければ黒が勝ちます。 明らかに、黒がN個の脅威で勝った場合、彼はN + 1でも勝ちます。 白人についても同様です。 これは、ソリューションが2つの数字の形式で記述できることを示しています。勝利するのに十分な黒の脅威の数(maxb)と、勝利するのに十分な白の脅威の数(minw)です。 そして、k個のco脅威を持つbの解を探しており、b minwとmaxbが以前の解決の試みから知られている場合、k <minw(白勝)とk> maxb(黒勝)の答えをすぐに返すことができます。 minw <k <maxb解決策を探す必要があります。
interface Results { minw: number; // white wins if nkt <= minw maxb: number; // black wins if nkt >= maxb } const tt: { [key: string]: Results } = {}; function solve(path: Board[], color: Color, nkt: number): Result { function solveFor(color: Color, nkt: number): Result { const board = path[path.length - 1]; const key = color + board; const cached = tt[key] || { minw: -Infinity, maxb: +Infinity }; if (color > 0 && nkt >= cached.maxb) return +1; // black has enough ko treats to win if (color < 0 && nkt <= cached.minw) return -1; // white has enough ko treats to win var result = -color; // that's a loss var depth = Infinity; // where repetition occured /* ... */ if (color > 0 && nkt < cached.maxb) cached.maxb = nkt; if (color < 0 && nkt > cached.minw) cached.minw = nkt; tt[key] = cached; return [result, depth]; } return solveFor(color, nkt); }
さて、外部の脅威を考慮して問題を解決するために、最初に脅威がないという仮定の下でそれを解決する必要があり(nkt = 0)、結果が変わるまでこのパラメーターを増減し続けます。 これは、理論的には決定グラフによって決定できます。見つかったソリューションが失われたkoに依存する場合、1つの外部ko脅威を追加して再度解決するのが理にかなっています。 実際には、私はこれをしませんでした。必要な脅威の数が1を超えることはほとんどありません。 解決するために2つのkoを獲得する必要がある問題がありますが、これはエキゾチックです。したがって、| nk2 | <2で解決した場合、一般に、問題は解決したと言えます。 このように、キャッシュを埋める最初のソリューション(通常はnkt = 0の場合)の検索に99%の時間が費やされ、その後、他のnktのソリューションが(JSでも)ほぼ瞬時に見つかることに注意してください。
それだけです。 最適化のないJS上のこのような単純なラティスは、すべての人(GCがロードするもの)に一時オブジェクトを作成し、各移動がボード全体をコピーする前に、数秒で合計10個の空きセルをすばやく解決できます(たとえば最初に見せたもの)。 少し大きくなると、ほとんどの場合、ハングし、GCをロードします。 ただし、アルゴリズムを高速化する方法はたくさんあるため、この種の最適化には意味がありません。
- 高度な深さ検索を適用します:dfpn、dfpnr、ldfpnr。 Mullerは、ldppnrは27個の空きセルでそれを圧倒できると書いています。
- 静的解析アルゴリズムを書く-まだBensonのアルゴリズムを実装していません。 誰が勝ったかが明らかな場合、これは検索を停止します。 これがおそらくすべてを迅速に解決できる主な理由です。通常、頭の中で解決策を見つけることは、評価で終わるいくつかの短いシーケンスを整理するように見えます。
- ボード上の何かを探す方法と移動する場所を考え出します。 これを行うには、自分の考えを「注意深く」注意深く観察し、何かを正確に見つける方法を理解するだけです。 もちろん、この探索の鍵は、グループが2つの目を作ることができるかどうかを判断することに基づいて、グループ(少数の密集した石)の活力を評価することです:それは常に、弱くて比較的大きなグループの近くに配置されます(そのため、それをキャプチャまたは保存するのに意味があります)
- スクイズ、ウェッジ、スナップバック、ラダー、ネットなどのトリックライブラリ(tesuji)を作成します。 これらのトリックは、心の中で解決策を見つける上で大きな役割を果たします。結局のところ、スナップバックを見つけるために可能なオプションをすべて計算するわけではありません-石の特徴的な組み合わせに気づき、このトリックから何かを絞ることができるかどうかを確認するだけです。
気にする人は 、 githubでコードを見ることができます。 率直に言って、速度を犠牲にすることなくモジュールに分割されるようにラティスコードを整理する方法を理解したらすぐに、すべてを書き換えてnafigする必要があります。など さて、単体テストを書くことができるように、そうでなければ、各変更の後、「このがらくたはまだ機能しますか?」