
Malte Lenzの投稿「 マシンガンジェットパック:ありえない飛行の本当の物理学 」。
こちらの投稿で説明したモデルを含むファイルをダウンロードしてください 。
翻訳に協力してくれたキリル・グゼンコに深く感謝します。
ショットから生じる反力を使用してマシンガンで飛行することは可能ですか? この質問は、 「もしもし? ランドールマンロー“ Machine Gun Jetpack ”(投稿のロシア語への翻訳 )。 一部の機械は自重を持ち上げるのに十分な力を生み出し、それ以上の力を発揮する可能性があるため、それが可能であることがわかります。 この記事では、ダウンファイアーマシンのダイナミクスと、この場合に速度とそれによってどれだけ高く登ることができるかによって発生する力を調べます。 また、記事の警告を複製します。これを自宅で繰り返さないでください。 このためのモデリング用のソフトウェア環境があります。
リスアサルトライフル
人よりも小さなものから始めましょう。 たとえば、この灰色のリスで。 リスをお尻に置き、自動モードでマシンから発砲し、何が起こるかを確認します。 このシステムのダイナミクスをシミュレートするには、 Wolfram SystemModelerを使用します。

機械モデル
上の画像では、マシンを見ることができます。 システムとしてのオートマトンは、カートリッジとオートマトン自体で構成され、さらに、それらはすべて質量を持ち、重力の影響を受けます。 組み込みの機械コンポーネントを単純に組み合わせることで、簡単に作成できます。

地球の重力の影響下にある質量
ストアはより複雑なコンポーネントです。ショットごとに、弾丸自体とスリーブの塊が放出されるためです。 各ショットで、弾丸の質量とスリーブの質量が、帯電したマガジンの質量から差し引かれます。 つまり、それらの質量にショット数を掛けたものが初期質量から差し引かれます。
これを単純なリスモデルと組み合わせ、地上の高さセンサーと、トリガーされるとシミュレーションを完了する衝突センサーを追加して、完全なモデルを取得します。
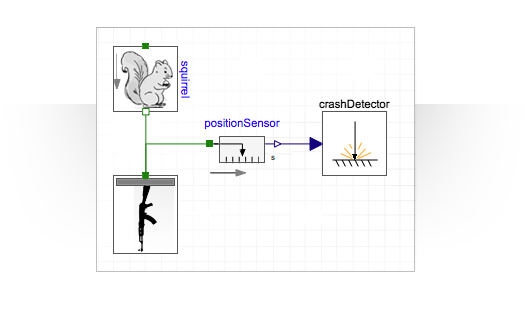
シミュレーションを正しく実行するには、さまざまなコンポーネントのパラメーター値を設定する必要があります。 灰色のリスを使用します。通常、重量は約0.5 kgです。

次に、マシン上のデータが必要です。 ユビキタスな7.62 mmカラシニコフ突撃銃(AK)を使用します。 詳細は次のとおりです。

マシンによって生成される推力は、弾丸の質量、銃口の速度、および1秒あたりのショット数に基づいて計算できます。

その後、各ショットの持続時間、つまり弾丸がバレルを通過する時間を推定することが可能になります。 バレル内の平均速度が銃口速度の半分に等しいという仮定を導入しましょう。

この時点での力は、トラクションを通じて計算できます。

これで、マシン上のタンパク質の飛行をシミュレートするために必要なすべてのパラメーターを設定しました。

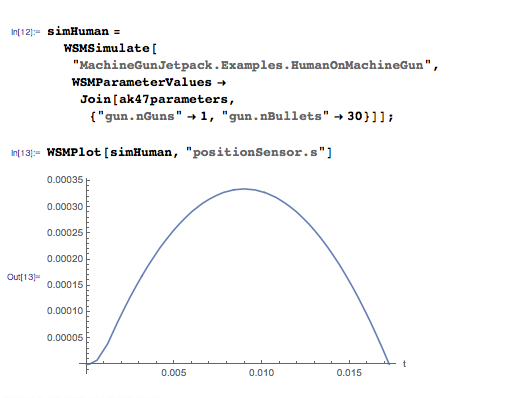
1つのカートリッジでタンパク質自動システムをシミュレートしましょう。

時間に応じて高度がどのように変化するかを考えると、リスが9センチの高さに達し、飛行時間が0.27秒になることがわかります。
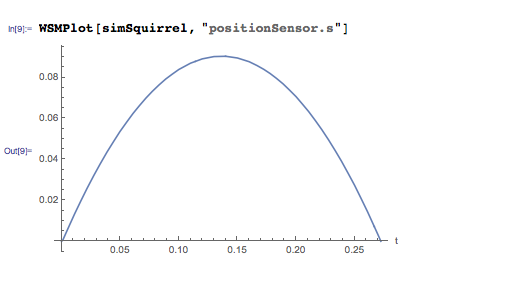
または、言い換えれば、

リスはあまり高くありません。 この問題の明らかな解決策は何ですか? もちろん、カートリッジを追加する必要があります。 標準ストアには30個が含まれています。

これにより約5.8秒の飛行が可能になり、リスはめまいがする高さ17.6メートルまで上昇します。 人にとって非常に恐ろしい身長ですが、おそらくリスにとってはそうではありません。

これがどれほど高い飛行をしたかです:

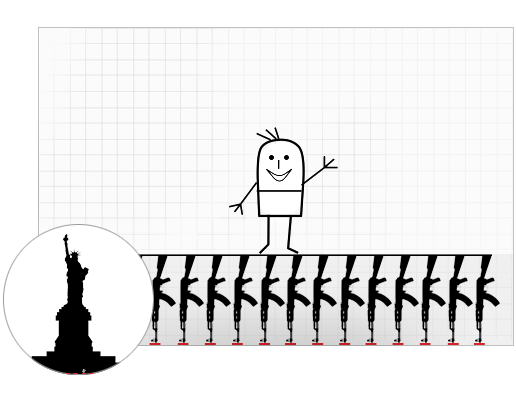
私は、リスが機械に座ったまま飛ぶことができることを示しました。 ここで、30ラウンドの雑誌を解除すると、男がどれだけ高く飛ぶことができるかを見てみましょう。
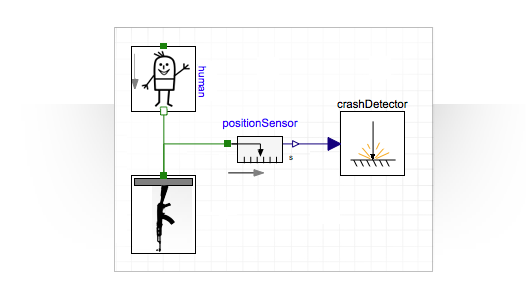
おそらく、1台のマシンでは十分ではありません。 あなたはそれらをもっと取る必要があります。 マシンの数に対応するパラメーターを導入し、1〜80の範囲の値を取ります。

ここには面白いことがあります。 50台以上のマシンの効果は簡単に説明できます。 それらが多いほど、出力が大きくなります。つまり、飛行高度は高くなります。 ただし、15台と32台のマシンでのシミュレーションはもう少し興味深いものです。 15台のマシンのオプションを詳しく見てみましょう。 赤い点はショットの瞬間に対応しています。つまり、マシンは100ミリ秒ごとにプールを撃ちます。
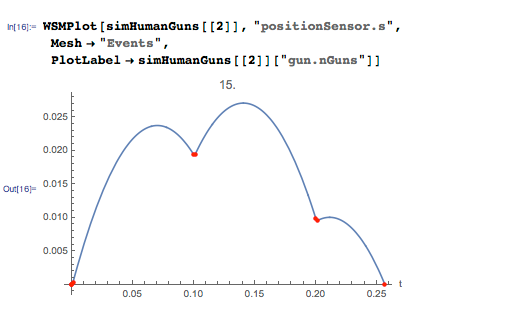
このシステム全体がわずかに上昇し、落下し始め、次のショットの後、再び上昇しますが、すでにわずかに高い位置にあり、前回よりも低く降下していることがわかります。 時間の経過に伴う速度の変化を追跡することもできます。
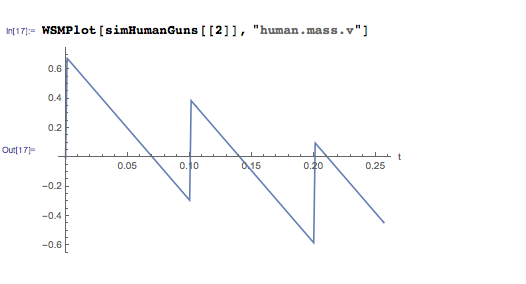
最初のショットまで、システム全体が地面にあり、したがって速度はゼロです。 その後、絶対速度は急激に増加しますが、次のショットがゼロ以下に落ちる前に。 つまり、次のボレーの後、速度の低下が発生し、その結果、システムは下降を開始しますが、まだカートリッジがストアに残っています。 しかし、その場からわずかなジャンプが発生します。
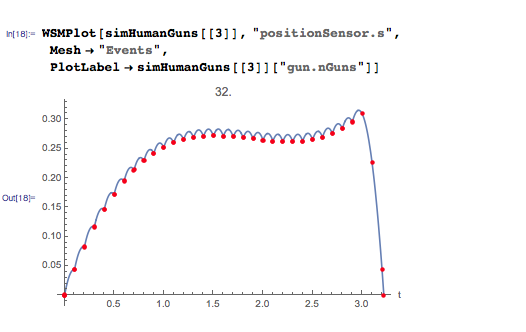
32台のマシンのシナリオでは、わずかに異なる動作が観察されます。 最初は15台の自動機を備えたシステムの動作に似ています-同じ段階的であり、各速度で絶対速度が失われ、その結果システムが急降下します。 ただし、開始から2.5秒後に、すべての弾薬が使い果たされるまでシステムは高度を上げ始めます。
これは、時間の経過とともにストアの質量が変化するためです。
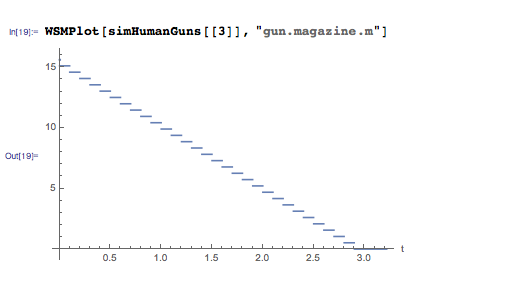
ショットごとにストアが重量を失うことがわかります-弾丸とカートリッジケースの質量。 このため、システムは軽くなり、高さを増し始めます。 これは、飛行能力を維持しながら各マシンに装備できるカートリッジの数に一定の制限があることを示しています。これは、変更可能な興味深いパラメーターです。 機械工場の次の能力で離陸してみましょう:

より多くのマシンが存在するほど、より多くのパワーが必要になるので、たとえば、1000個を取りましょう。

1000発の機関銃を使用する場合、165ラウンドごとに供給することは最良の選択肢ではないことがわかります。

これは、弾丸の数が多すぎると、システムが重くなりすぎて飛行できなくなるためです。 合理的な(この言葉が自動機での飛行に一般的に当てはまる場合)飛行回数が得られたので、マシンガンの数を変更することで達成できる高さを見てみましょう。 マシンが多ければ多いほど、飛行は高くなり、飛行時間は長くなると予想されます。

最大高さのマシン数への依存性は次のとおりです。
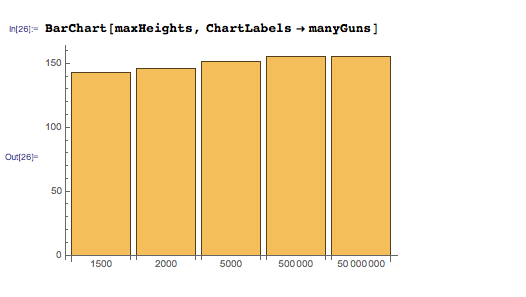
結局のところ、マシンの数が大幅に増加すると(1,500から5,000万)、最大高さはわずかに増加します。 これは、マシンの数が増えると、各マシンの人の比重が小さくなり、各マシンがわずかな質量を追加して自身の質量を上げるだけになるためです。 システムは、1台のマシンと同じ最大高さに達することができますが、追加の質量はなく、マシンの数が増えると利点がなくなります。
上記を要約すると、自動機の最高のジェットエンジンには、店内に145カートリッジの5000 AK以上が含まれている必要があります。
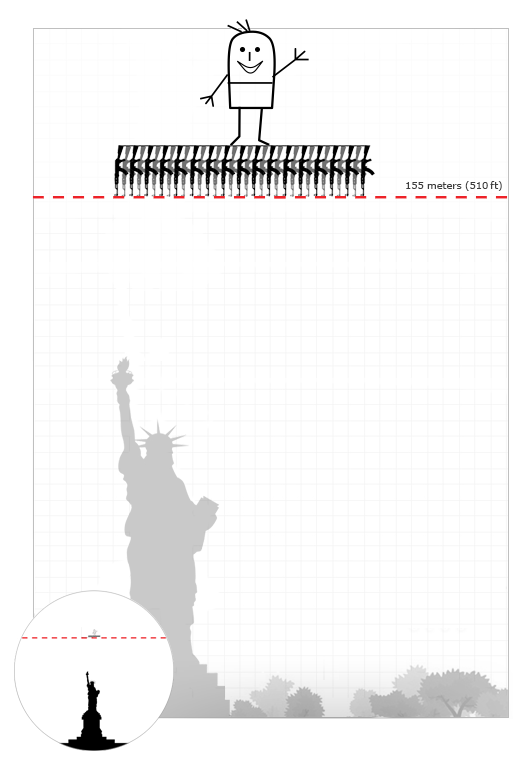
自動機でどれだけ高く飛べるか