特別な機能の歴史と未来

Stephen Wolframの記事「 The History and Future of Special Functions」の翻訳。

翻訳に協力してくれたキリル・グゼンコに深く感謝します。

---

この記事は、 オレグ・マリチェフの60歳の誕生日を記念するイベントの一環として、イリノイ州シャンペーンで開催されたWolfram Technology Conference 2005で行われたスピーチの録音です。



それで、今、私は今朝取り上げたトピックに戻りたいと思います。 特殊機能の過去と未来についてお話したいと思います。 少なくとも過去30年間、特別な機能が私の情熱の主題でした。 そして、私の仕事は特別な機能の使用を促進する上で大きな影響を与えたと思います。 しかし、私は以前にこのトピックを取り上げたことがなかったことがたまたま起こりました。 今、それを修正する時間です。





数学の多くの概念とオブジェクトの歴史は、古代バビロンの時代にまでさかのぼることができます。 実際、4000年前のバビロンでも、さまざまな複雑な演算を行う60進演算が開発され、積極的に使用されていました。



当時、加算と減算の操作は非常に簡単であると考えられていました。 しかし、これは乗算と除算の操作には適用されませんでした。 そして、そのようなアクションを実行するために、特殊機能のいくつかの類似性が開発されました。



実際、除算は、逆値の加算と減算に削減されました。 そして、かなりcな方法での乗算は、平方の加算と減算に帰着しました。



したがって、ほとんどすべての計算はテーブルの操作に帰着しました。 そして、もちろん、考古学者は逆数と二乗の表を持つバビロニアの粘土板を見つける機会がありました。



つまり、バビロニア人は、繰り返し使用できる数学的または計算的な作業がいくつかあり、非常に有用な結果が得られるという考えをすでに持っていました。



そして、ある程度まで、特別な機能の歴史は、これらの「ピース」からシーケンスを操作する原理の発見から始まります。



次の「ピース」は、おそらく三角法を含むものでした。 エジプトのパピルスリンダ1650 BC ピラミッドに関するいくつかの問題がすでに含まれていましたが、その解決には三角法が必要でした。 交霊表のあるバビロニアのタブレットが見つかったことに言及する価値があります。



もちろん、エピサイクルモデルを使用した当時の天文学者は、すでに本格的に三角法を使用していました。 そして、再び、すべての数学的操作は、少数の「特別な」関数を扱うことになりました。



彼らがコードやアークと呼んでいるものに多くの注意が払われました。 これが写真です。











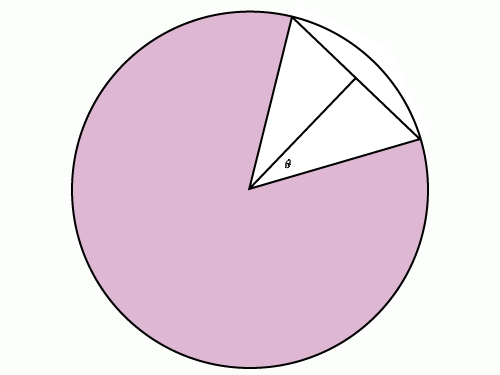
2つの単位円半径があり、それらの間には一定の角度があります。 それらの間の和音の長さは？ ここで、コードの長さの角度のマッピングを角度のサインの関数と呼びます。



そして、ここに逆の問題があります。特定のコード長に対して-角度はどうなりますか？ 間違いなく、今ではアークサインと呼んでいます。



ギリシャの天文学者はこれらの和音と弧を非常に真剣に受け止めました。 プトレマイオスのアルマゲストはそれらでいっぱいです。 そして、彼らは言う、紀元前140年頃 ヒッパルコスはコード表付きの12巻を収集しました。



さて、三角法に関するアイデアはバビロンとギリシャから広まり始めました。 三角法はさまざまな標準とルールを迅速に獲得しました。 ヒッパルコスはすでにバビロニア人から360度の円という考えを採用しています。



そして、文字通りアラビア語に翻訳されたラテン語に誤って翻訳されたインド語の「コード」から、「サイン」という単語が登場しました。 12世紀で、13世紀の初めにフィボナッチは積極的に使用し始めました。



14世紀には、三角法が普及しました。 そして、16世紀の半ばに、彼女はコペルニクス- デレボリューションバスの仕事で非常に重要な役割を果たしました。 この仕事は長い間、数学関数を扱う人々にとって基本的なものになりました。



そのとき、三角法はほぼ完全にモダンな外観になりました。 もちろん、いくつかの重要な違いがあります。 たとえば、バーシナスの絶え間ない使用。 誰もこれを聞いたことがありますか？ 基本的に、これは1-Cos [x]です。 それはごく最近まで公開されていた三角表で見つけることができます。 しかし、今ではいくつかの余分な算術演算はまったく問題ではないので、この関数についてはもう話すべきではありません。



さて、三角法の後、次の大きなブレークスルーは対数でした。 1614年に登場しました。











これは、乗算および除算を加算および減算演算に減らす方法でした。



長年にわたり、対数を持つ多くのテーブルが登場しました。 実際、テーブルの使用は、300年以上にわたって存在していたユビキタス標準になっています。



自然対数と指数が現代の形を見つけるのに数年かかりました。 しかし、17世紀の半ばには、私たちに馴染みのある基本的な機能がすべて登場しました。 そしてそれ以来、今まで、それらは実際、ほとんどの人が知っている唯一の明示的な数学関数です。



まあ、17世紀の終わりに微積分が現れたことがわかります。 そして、これが現代表現の特別な機能が現れ始めた時です。 それらの多くはすぐに登場しました。



18世紀のどこかで、ベルヌーイの1人は、おそらく基本関数の積分も基本関数になるという考えを提唱しました。 ライプニッツは反例があると思った。 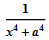。 しかし、この表現はそうではありませんでした。 数年间、 楕円積分の活発な議論がありました。 少なくともシリーズに関しては。 そしてベッセルの機能が発見されました。



そして、18世紀の20代までに、オイラーはコンピューティングの世界に突入し始めたばかりでした。 そして、彼は私たちの標準的な特別な機能の多くについて書きました。



彼は、 ガンマ関数を階乗概念の発展として発見しました。 彼はいくつかのアプリケーションでベッセル関数を定義し、 楕円積分を研究し、 ゼータ関数を導入し、 多対数を研究しました。



通常、彼は関数に特定の名前を付けませんでした。



しかし徐々に、彼が書いた機能がさまざまな人々によって使用されるようになりました。 また、多くの場合、一定期間使用した後、特定の指定と名前をすでに受け取りました。



特別な機能の出現には、さらにいくつかのアクティビティのバーストがありました。 18世紀の終わりには、潜在的な理論と天体力学がありました。 また、たとえば、長い間ラプラス関数と呼ばれていたルジャンドル関数は、1780年頃に登場しました。 1820年代には複雑な分析が一般的になり、さまざまな2周期関数が出現し始めました。 当時、この分野で人々の間のコミュニケーションが十分に確立されていたとは言えません。 そのため、最終的には、同じ概念のさまざまな互換性のない表記が登場しました。 その時に現れた問題は今日でも関連があり、しばしばMathematicaサポートへの呼び出しを引き起こします。



数年後、高調波解析が勢いを増し、さまざまな直交多項式（エルミート、レイグラなど）が得られました。



さて、すでに19世紀の初めには、特殊な機能の「動物園」全体が現れていたことが明らかでした。 そして、それはガウスにそれをすべてまとめる方法を考えさせました。



彼は超幾何学シリーズを調査しましたが、実際にはウォリスによって1650年代に既に開かれており、彼の名誉にちなんで名付けられました。 そして彼は機能に気づいた 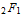（ ガウス超幾何関数 ）実際に多くの有名な特殊関数をカバーしています。



19世紀半ばまでに、特にドイツで特別な機能に多くの注意が払われました。 この時点で、このトピックに関する多くの文献が登場しました。 したがって、マックスウェルが19世紀の70年代に電磁気理論に関する研究を書いたとき、彼は特別な機能の数学的装置に多くの時間を割く必要はありませんでした。 参照できる文献はすでにたくさんありました。



関数のプロパティを説明する純粋に科学的な論文に加えて、それらの値を持つテーブルも作成されました。 誰も実際に聞いたことがない人もいます。 そして、時には非常に有名です-ヤコビ、エアリー、マックスウェルなど。



したがって、19世紀の終わりのずっと前に、今日私たちが扱うほとんどすべての特別な機能がすでに作成されています。 しかし、他にもありました。 たとえば、 グデルマニアンとは何か聞いたことがありますか？ 私が子供の頃参考書で彼に会った方法を覚えています。 グデルマニアンは、ガウスの生徒であるクリストフ・グーダーマンにちなんで名付けられました。 三角関数と双曲線関数との関係を確立し、メルカトル図法の投影と密接に関連しています。 しかし、グデルマニアンは現代文学にはほとんど見当たりません。



さて、19世紀の最後の数十年間に、特別な機能の開発に大量の知的資源が投資されてきました。 私は、すべてが不変式、シジーの理論の方向、またはビクトリア朝時代の他の特徴的な数学的願望に向かって発展したと信じています。 実際、抽象化と一般化に対する純粋な数学の典型的な愛は、特別な機能をarbitrary意的なものにし、特に結び付けていません。 それは、一般的な生化学を研究する代わりに、動物園で奇妙な動物を研究するようなものです。



ただし、理論物理学の進歩により、特殊機能への関心が再び高まっています。 メカニズム。 弾性の理論。 電磁理論。 その後、1920年代の量子力学では、最も基本的なタスクでさえ、ラジェラ 多項式やエルミート多項式などの特別な関数を使用する必要がありました。 そして、散乱の理論がありました。それは、おそらく、ほぼすべての特別な機能の「動物園」を使用していました。



これにより、純粋な形の問題は何らかの形で特別な機能に関して常に解決できるという考えが生まれました。 そして、間違いなく、教科書はこの考えを促進しました。 それらで議論された問題は、特別な機能に関して非常に簡潔に定式化されたからです。



もちろん、いくつかのギャップがありました。 5次の多項式。 3つの団体の仕事。 しかし、それらはあまりにも非標準でした。 現代の確率論に必要なものではありません。



一般に、特殊機能の範囲は非常に広範囲です。 特にイギリスでは、テーブルの作成が非常に勢いを増しています。 実際、この地域は国家にとって戦略的に重要でした。 特に、ナビゲーションのようなもののために。 多くのテーブルが公開されました。 ここでは、例えば、1794年からの良い選択。 初めて見たとき、ここにはある種のタイムシフトの場所があると思いました。









（実際、このウルファムはベルギーの砲兵隊の将校でした。私は彼と親haveを持っているのは、7世紀に住んでいた聖ウルフラムほどではないと思います）。



当時はテーブルが重要な役割を果たしていたため、1820年代に正確なテーブルをコンパイルするために設計されたバベッジ差分マシンが登場しました。 そして、19世紀の終わりまでに、特別な機能が編集の基礎になりました。



機械式計算機はますます普及し、英国と米国では、特殊な機能のテーブルを作成する大規模なプロジェクトがありました。 たとえば、30年代のWPAプロジェクト（ Works Progress Administrationプロジェクト ）のように、大恐duringの間に人々は数学関数の値の計算に忙しかった。



その後、彼らの財産を体系化する真剣な仕事が始まりました。 それぞれに多くの作業がありましたが、それぞれの貢献はそれほど大きくありませんでした。 誰もが自分が重要な役割を果たしていると思っていましたが。 ちなみに、1909年に最初に出版され、30日にはイラストを手に入れたアメリカのヤーンケとエムデの表紙です。











ちなみに、まったく悪くありません。











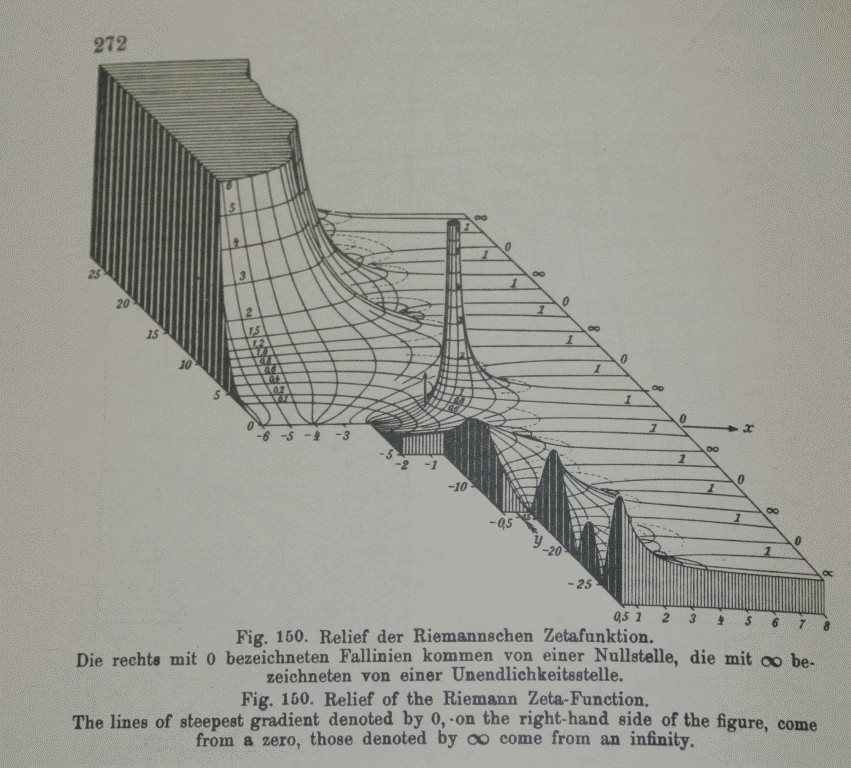
20世紀の初めには、石膏と木材から機能の体積モデルを作成することが一般的でした。 そして、はい、ゼータ関数を説明するアイデアがありました。これは、ヤーンケとエムデによるMathematica Bookの初版をカバーするために使用していました。











第二次世界大戦中、特殊機能に関する多くの研究がありましたが、その理由を説明するのは困難です。 これはおそらくいくつかの軍事的ニーズが原因でした。 しかし、私はそれが単なる偶然であると信じたがっています。 ただし、一部の戦略的活動との潜在的なリンクを否定すべきではありません。



そして、マグヌスとオーバーヘッティンガーの初版は1943年に出版されました。











それに基づいて、 Gradstein-Gingerの初版が登場しました 。



1946年、ハリー・ベイトマンは死亡し、特別な機能に関するすべての情報の大規模なアーカイブを残しました。 最終的に、彼の業績は、Bateman Manuscript Projectという名前で公開されました。



マンハッタンプロジェクト、およびその後の水素爆弾開発プロジェクトも、特別な機能の顧客および消費者としての役割を果たしました。 たとえば、1951年に、国家標準局のMilt Abramowitzは、核物理学に必要なクーロン波動関数の表を作成しました 。











これから、1965年に出版されたAbramowitz-Steganの本が徐々に成長し、特別な機能を使用するアメリカ人にとってナンバーワンの文学になりました。











60年代および70年代には、コンピューターの数値アルゴリズムの開発に多くの注意が払われました。 そして、特殊機能の計算はお気に入りの場所でした。



ほとんどの場合、作業は非常に具体的でした。特定の計算精度で特定の次数の特定のベッセル関数に膨大な時間を費やすことができました。 しかし、特殊な関数を計算するための特定のアルゴリズムのコレクションを備えたライブラリが徐々に登場しました。 ただし、多くの人々は依然としてテーブル付きの参考書を使用しています。これは、科学図書館の最も著名な場所でよく見られます。



私がまだティーンエイジャーだった頃、私は1970年代半ばに特別な機能に従事し始めました。 イギリスの学校で学んだ公式の数学は、特別な機能を意図的に避けていました。 基本的な機能のみを使用して答えを見つけるために、いくつかのトリッキーなトリックを使用することにありました。 あまり好きではなかった。 もっと一般的で実用的なものが欲しかった。 ずるい。 そして、私は特別な機能のアイデアが好きでした。 彼らはより効果的なツールのように見えました。 しかし、数理物理学の本での彼らの議論は、十分に体系的とは思えませんでした。 はい、それらはより強力な機能でした。 しかし、彼らはまだややarbitrary意的でした。印象的な音の名前を持つ好奇心の強い生き物の動物園のようなものです。



いくつかの実際のタスクのために特別な機能を使い始めたとき、私は16歳だったと思います。 それは二対数でした。 彼は素粒子物理学で働いていました 。 そして、私はそれを単にfと指定したと言って恥ずかしく思います。











しかし、私の防衛では、多対数は実際には研究されていなかったと言えます。 数理物理学に関する通常の本には、ベッセル積分、楕円積分、直交多項式、さらには超幾何関数が含まれていました。 しかし、多重対数はありません。 結局のところ、ライプニッツはそれらについて書きました。 しかし、何らかの理由で、彼らはおなじみの特別な機能の「動物園」に分類されませんでした。 そして、1970年代半ばに見つけることができたそれらに関する唯一の本当の情報は、エンジニアのレナードルーウィンによる1959年の電子レンジに関する本にありました。



その後まもなく、ファインマン図の積分を計算しなければなりませんでした。 そして、ポリログが鍵であることに気付きました。これがあなたが必要とするものです。 多対数は私の忠実な友人となり、私はそれらの特性を研究し始めました。











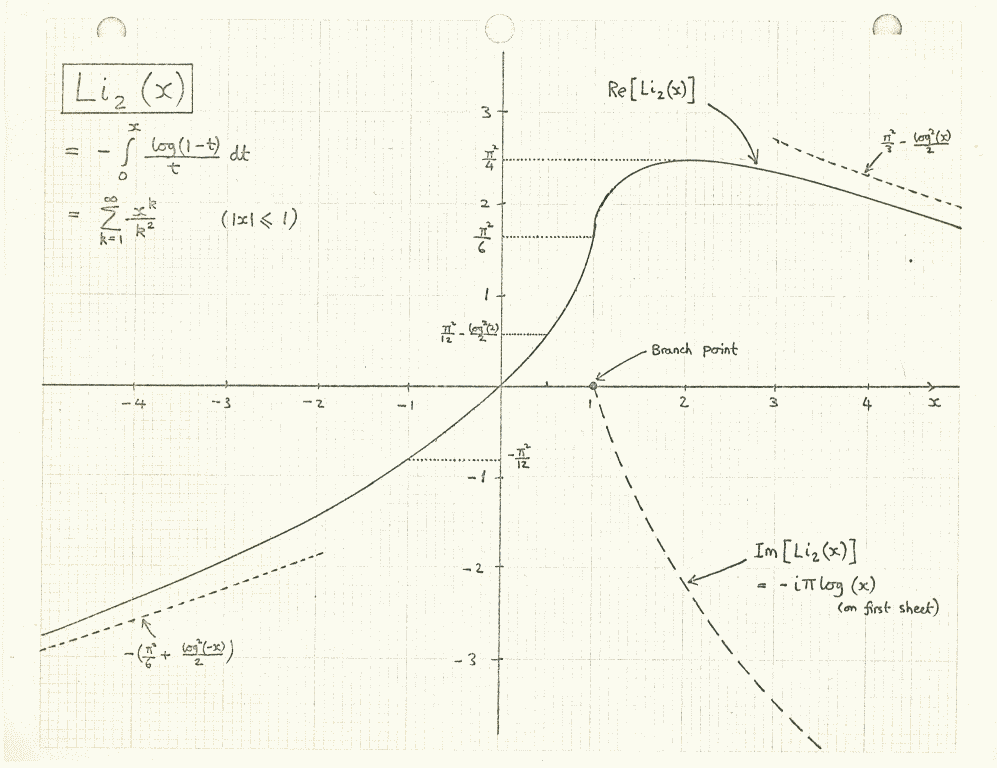
そして、その時に気づいたことがありましたが、その意味は、かなり後になって初めて実感しました。 , -.



, , - . - , , . - . . , -.



, , - , . . , .



, - 78- , . - Macsyma, .











. .











, . K- , .











- . " ", . .



, 1- . .



, - . — , . .



— - - . . , . , , .



- , - , , , - . , . -, 1970-, , «» .



- . . , . , ( , ). , -.



, . , , , . , . , , -.











, , . 1936- , - ( ). 1941- — - , - . 43- - ( , ). . , , , , : 1858- , 1894- 1922-. s , 。 . , . , , .



, . 1899 . 1948 . , . . , . , -.



1958 . , , - - , .



, - 1953 , , , . . , . - — .



, — - . . , , , .



, , 1970- . , 1979 , SMP — Mathematica , . — .



SMP, . .











.











SMP 1981- .











. , . . , , , . . . , — . .



, . 1986 Mathematica . — , , , .



, , , . , - . , . . : " , , 90- ".



, . , , . , . . A New Kind of Science — . .



, . .



, , , Mathematica . — . . , , . . . , .



, , , , , . FunctionExpand FullSimplify . .



. , . , , , , .



, . , . — . . , , 。











. , , . , , .



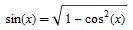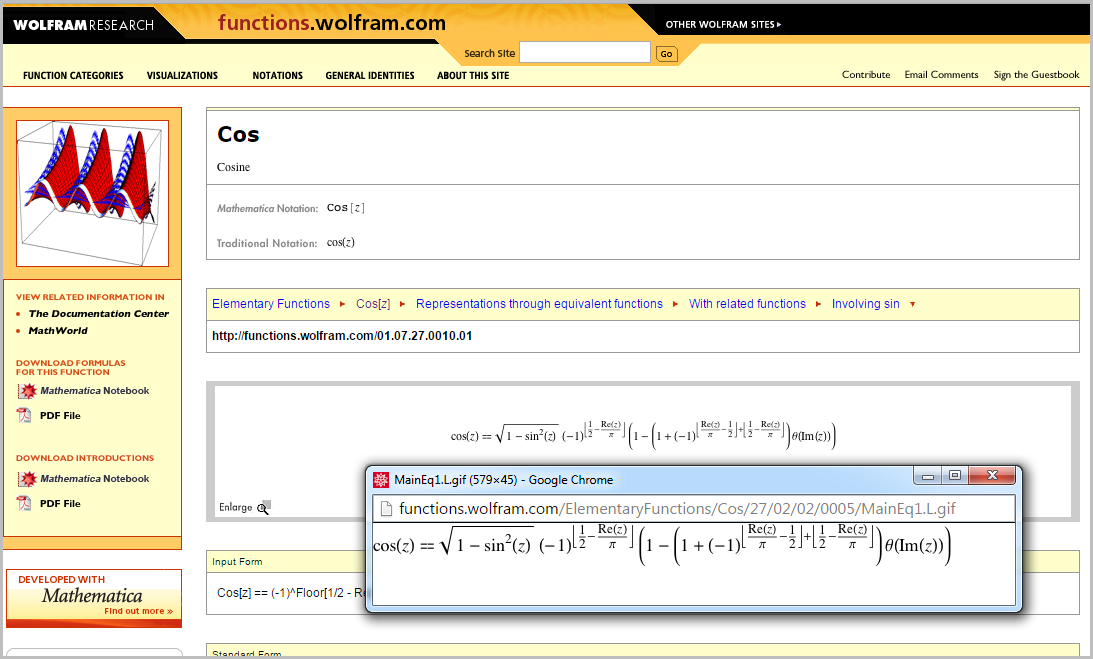
, Mathematica . . . , Wolfram Functions Site . - , .



, . - , , , , , , . - , . - ( Wolfram|Alpha , . .). - . .



, . . , . . , , , , . , . . . Mathematica .



, Mathematica , . ? , , .



, Mathematica , — , . RSolve Sum DSolve Integrate . , , . 1859- 1860- — : A Treatise on Differential Equations A Treatise on the Calculus of Finite Differences . Mathematica .



, , , . . , , , 17- .



. , .



: . . , .



Wolfram Language ( Mathematica ). , . Mathematica , , .



? . ? , Mathematica, Wolfram Functions .



. -, . — . . .



, , . , . , , .



: - ? ? ? , Wolfram Functions Site. , , Wolfram Functions Site.











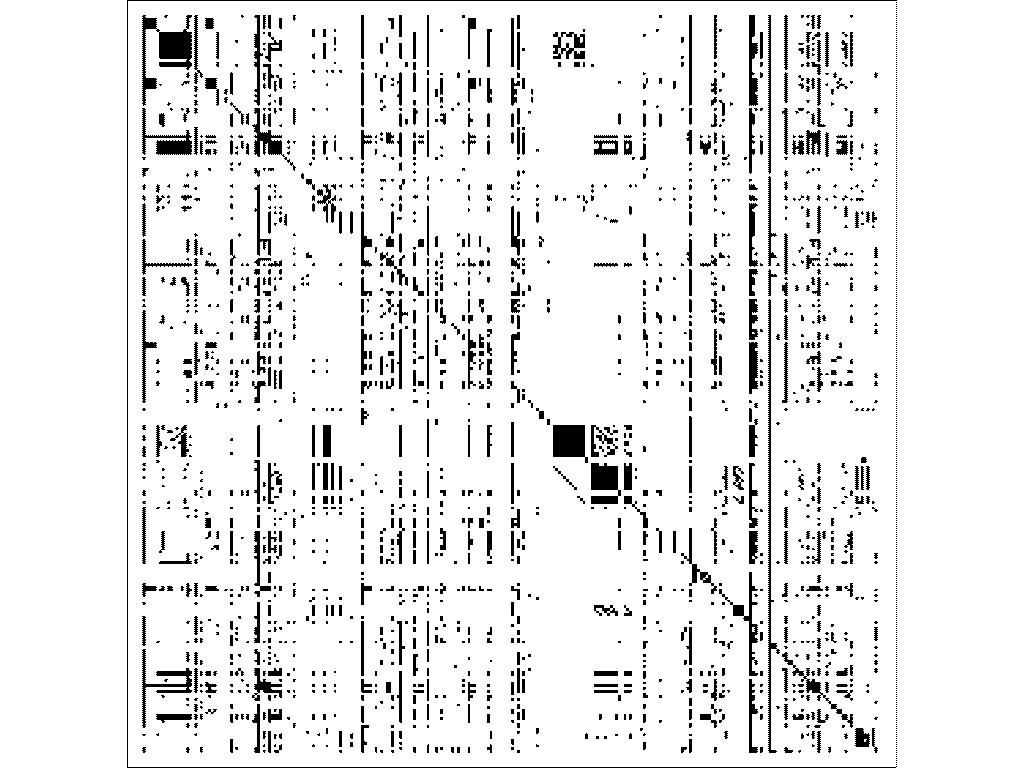
, Google-pagerank-.











, .











, , . , , . , , . - .



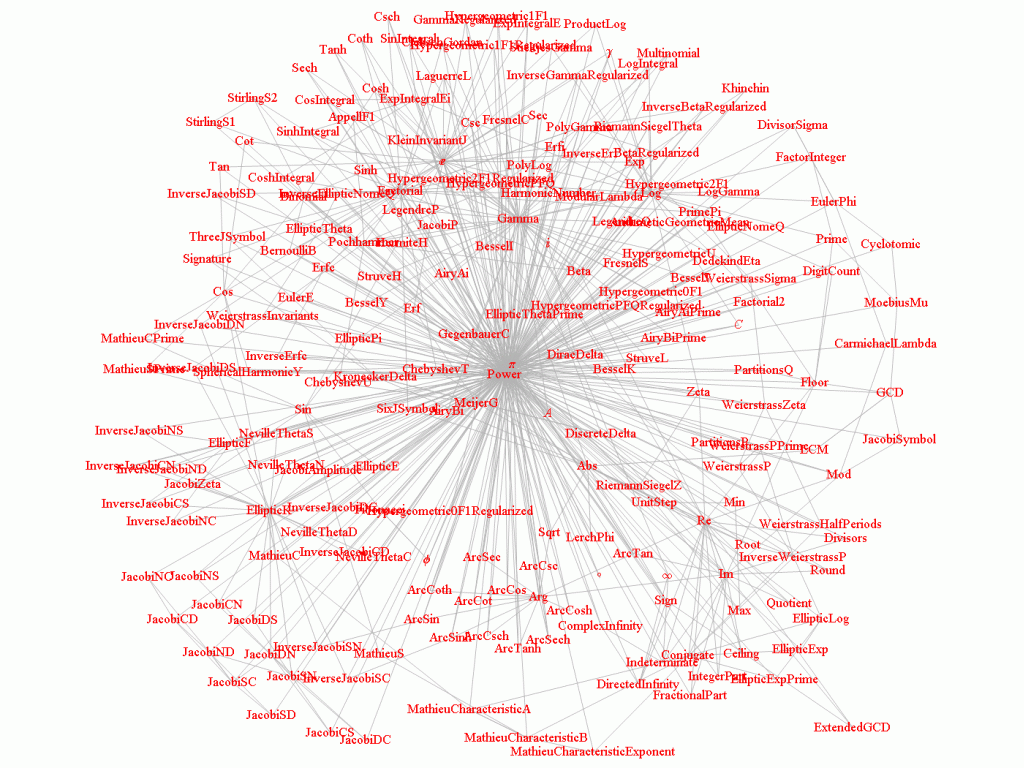
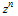, , . , . , , , , , — . n . , . — .



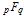p q - , . (Power) {0,0}. — {1,0}. (Erf) — {1,1}. BesselJ — {0,1}. EllipticK — {2,1}. 6- j — {4,3}. , , . , .



, : - , , , — . , .



— . Sum Mathematica . :











, 。 — - . 。



, , .



, . : , .



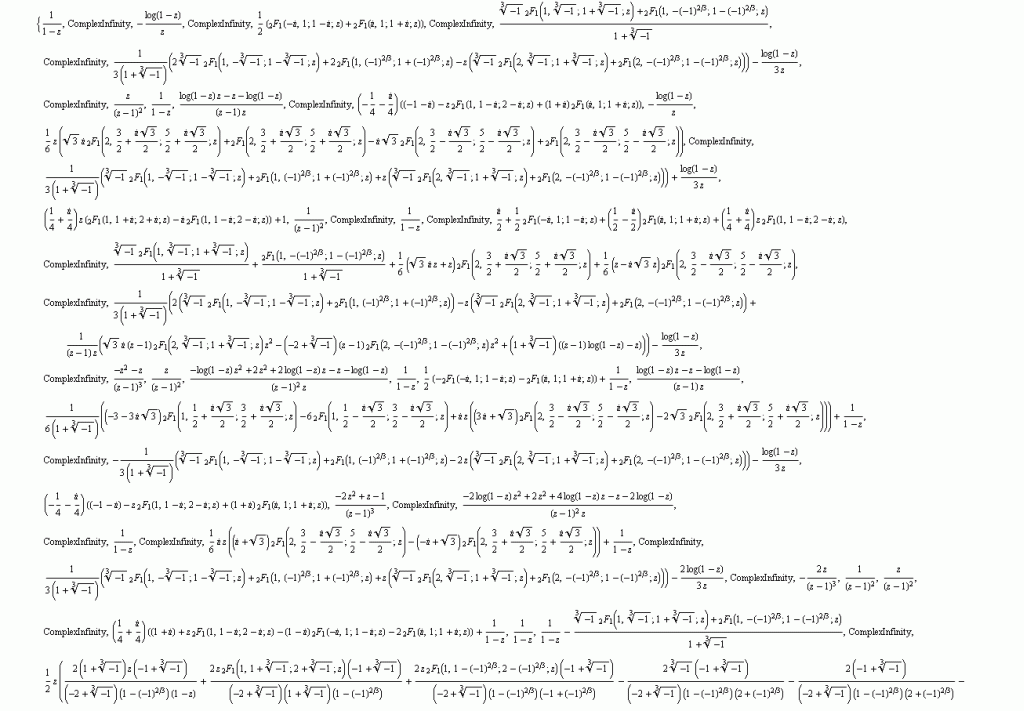
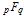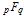, , . , , , , . DSolve . .











. . - .



- . DSolve . . — DSolve ? , . - , .



, , . . , , Sin[Sin[x]] . , . . . , .



. Integrate Mathematica , . , , .



- : , ? , , , . . . . , , .



. . , , , , - . , . . .



? , ?



. , , .



, — . . , . — — . .



? . , .











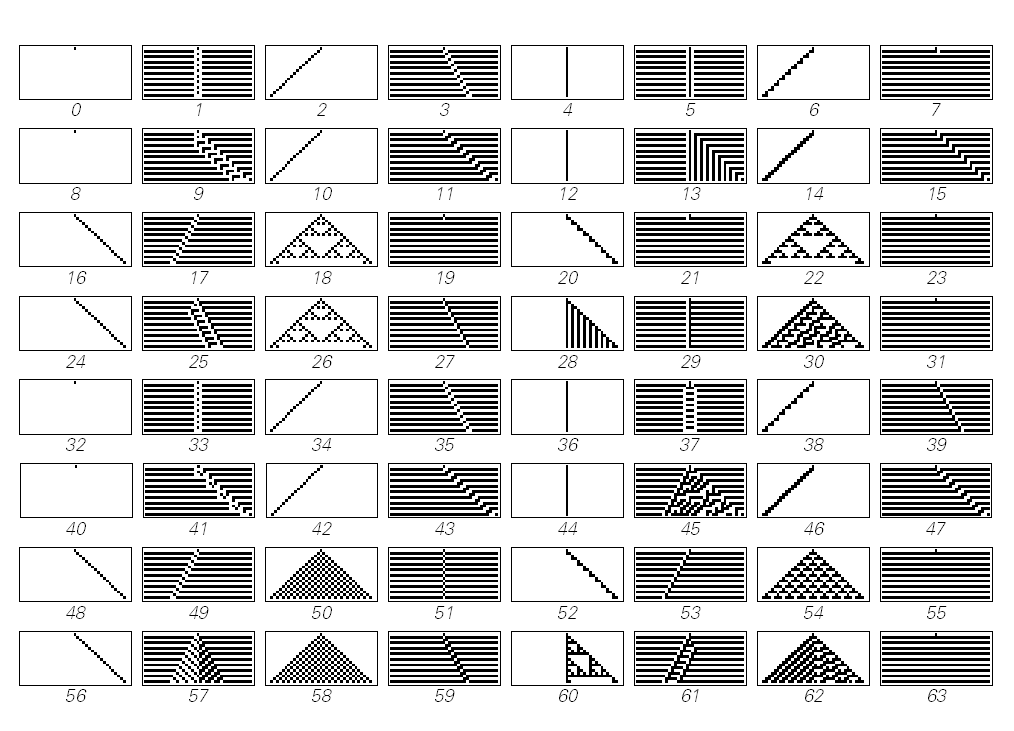
多くはかなり単純なことをします。そして、彼らは同じ構造を与えます。または少なくとも繰り返し。



これを実装するための式が見つかると想像してみましょう。これを使用すると、たとえば、特定のセルが特定のステップでどの色になるかを理解できます。



しかし、この男はどうですか？私のお気に入りの30番目のルールは？











一定回数の反復後に何が起こるかを決定する公式はありますか？



またはこれのために？











そうは思いません



実際、そのようなシステムは本質的に計算上既約ではないと思います。



このようなシステムは、何らかの計算プロセスとして30番目のルールと見なすことができます。 どのような結果が得られるかを予測しようとする場合、いくつかの計算も実行する必要があります。 そして、ある意味では、理論物理学などの伝統的な分野の成功は、実際、私たちが研究しているものよりもはるかに複雑なシステムの解決に基づいていました。 そのため、必要以上に計算能力が低い場合にシステムが何をするかを定義する必要があります。



はい、私の本の主なアイデアの1つは、私が計算的等価性の原則と呼ぶものです。 この原則は、動作が明らかに単純ではないほとんどすべてのシステムが、計算の複雑さと正確に同等であることを示しています。 私たちの脳と数学的アルゴリズムはどちらも非常に複雑なルールで機能しますが、たとえば、30番目のルールよりもやや複雑な計算を実行することはできません。 つまり、これは、30番目のルールの動作が計算上既約であることを意味します。単に30番目のルールを再現するよりも効果的なプロセスを使用してシステムがどのように動作するかを説明できません。



したがって、30番目のルールの正確な解を得ることができません。たとえば、引数がセルの座標とステップであり、関数の出力がセルの色である式です。



ところで、30番目のルールの計算の普遍性を証明すれば、これを証明できます。つまり、その助けを借りて計算を実行し、システムをエミュレートできます。 そして、これはこのルールが正確な解決策を持たない理由を理解する方法です。 いくつかの点で、このソリューションは可能な計算でなければならないからです。 つまり、ある種の小さな式にはなりえないということです。



さて、特別な機能に関するこれから何が続きますか？ さて、大量の計算上の既約性に直面している場合、特別な関数はあまり役に立ちません。 多くの問題では、ある種の数式を作成することは不可能だからです-特別な機能などは関係ありません。



私の本の主なアイデアの1つは、さまざまなプログラムのコンピューティングの世界では、計算の既約性の問題が非常に簡単に解決されるということです。 そして、私たちがめったに遭遇しない理由は、理論物理学などの知識の領域が計算上の既約性を特に避けるためです。



しかし、自然界、特に生物学などの分野では、コンピューティングユニバースの代表者のより広範なサンプルに遭遇する可能性があります。 つまり、計算上の既約性を見つけることができます。 理論科学はこの分野ではあまり進歩できませんでした。



さて、今度は30番目のルールのようなシステム、または、考えられるすべての類似した方程式の空間を探索しながら見つけた小さな偏微分方程式を見てみましょう。











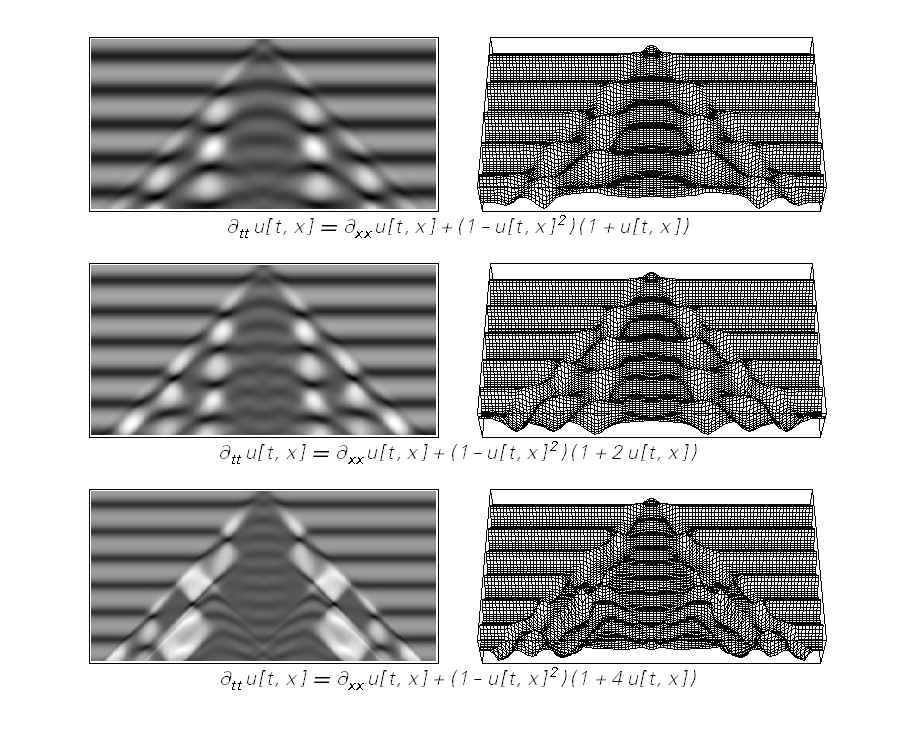
それでは、なぜこれらのシステムで起こっていることを反映する高レベルの特別な機能が存在しないのでしょうか？



もちろん、30番目のルールに特別な関数を設定することもできます。 または、このUDCの特別な機能。 しかし、これは一種の欺ceptionです。 そして、私たちがたどるパスは、特別な機能があまりにも「特別」であることを明確にします。 もちろん、純粋に名目上、これにより30番目のルールまたはこのURChPの使用が加速されます。 しかし、それだけです。 ベッセル関数のように、無数の異なるタスクで出現することはありません。 この特定の問題を解決するためだけに役立ちます。



上記を要約してみましょう。 事実、計算上の既約性のある特定の領域がある場合、それを避けることができる多くの別個の領域があるということです。 役に立たない特別な関数の意味は、多くの異なる問題がこの特別な関数に簡単に降りてくることです。



計算上の既約性がないすべての問題の範囲には、超幾何型の標準的な特殊関数が含まれることがわかります。 そして、この領域を超えたものは何ですか？ 計算上の既約性に満ちていると思います。 そして断片化に満ちています。 そのため、多くの問題領域をすぐにカバーする新しい魔法の特殊機能は表示されません。 これは、ソリトンなどの状況に少し似ています。 彼らはそれぞれの分野で優れていますが、非常に具体的です。 彼らはあらゆる種類のタスクのスペースの非常に狭い領域に住んでいます。



では、これらの概念をより一般的にどのように定式化するのですか？



さまざまなシステムの特殊機能の類似物を考えるかもしれません。 いくつかの計算を必要とする可能性のある特別なオブジェクトの限られたセットはありますが、その助けを借りて、他の有用なオブジェクトを取得することが可能になりますか？



あなたは数字を考えるかもしれません。 数値は、「基本」、有理数、代数にできます。 しかし、役に立つ「特別な」数字は何でしょうか？ もちろん、これらはPi 、 E 、およびEulerGammaです。 他の定数はどうですか？ 残りの定数は、より有名な同等物の影に消えます。 Wolfram Functionsのウェブサイトには、定期的にポップアップする定数が存在するが名前のない例はおそらくないでしょう。



[この場所で演奏の録音が終了します]

---

Wolfram言語（Mathematica）の第10バージョンには何百もの特別な機能が組み込まれています。



ここでそれらについて詳しく知ることができます：

• Wolfram言語（Mathematica）で実装された特別な関数のリスト （グループごと）
• Wolfram言語の特別機能ドキュメント