単純な接尾辞ツリー

サフィックスツリーは、非構造化データ配列での無数の複雑な検索タスクを予想外に効果的に解決できる強力な構造です。 残念ながら、よく知られているサフィックスツリー構築アルゴリズム（主にEsko Ukkonenによって提案されたアルゴリズム）は、理解するのが非常に複雑であり、実装に時間がかかります。 比較的最近になって、2011年にDany BreslauerとGiuseppe Italianoの努力により、比較的簡単な構築方法が発明されました。これは、実際に、1973年に接尾辞木を発明したPeter Weinerのアルゴリズムの簡略版です。 接尾辞ツリーが何であるかわからない場合、または常にそれを恐れている場合、これはそれを研究し、同時に比較的単純な構築方法を習得するチャンスです。



サフィックスツリーの説明に進む前に、用語を定義します。 アルゴリズムの入力は、n文字s [0]、s [1]、...、s [n-1]で構成される文字列sです。 各文字はバイトです。 もちろん、ここで説明するすべては、ビット、2バイトUnicode文字、DNAシーケンスの2ビット文字など、他のシーケンスでも機能します。 さらに、s [n-1]は文字0と等しいと仮定しますが、これはsの他のどこにもありません。 この最後の制限は、物語を単純化するためだけのものであり、実際、それを取り除くだけで十分です。 s [i..j] = s [i] s [i + 1] ... s [j]という形式の行（iとjは整数）は、通常どおり、部分文字列と呼ばれます。 s [i..n-1]という形式の部分文字列（iは整数）は、サフィックスと呼ばれます。



だから、主人公。 文字列sの接尾辞ツリーは、頂点の数による最小ツリーであり、各接尾辞s [i..n-1]がルートから特定のシートへ、またはその逆で読み取れるように、各エッジに空でないサブストリングsがマークされます。 、ルートからリーフへのパスで読み取られる各行はサフィックスsです。 この定義を処理する最も簡単な方法は、たとえば（現時点では、pos、len、およびtoに注意しないでください）です。





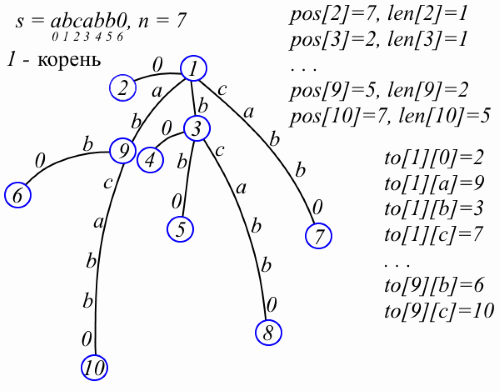
接尾辞ツリーにある頂点は2n + 1以下です。 サフィックスを連続して挿入してツリーを構築する場合、これを確認できます。次のサフィックスを挿入すると、新しいリーフとこのリーフがアタッチされる頂点が表示されます。 s [n-1]は特殊文字であるため、接尾辞ツリーには正確にn個の葉があります。 頂点に整数で番号を付けます。 頂点vの父をパー[v]に保持します。 vからファザーvまでのエッジのラベルは、数値のペアとして格納されます。ラベルの長さlen [v]と、このラベルの直後の位置pos [v]は、sにあります。 ラベルが文字列tの場合、t = s [pos [v] -len [v] .. pos [v] -1]。 頂点vにk個の子があり、t ₁ 、t ₂ 、...、t _kがvから子までのエッジ上のラベルであるとします。 行t ₁ 、t ₂ 、...、t _kの最初の文字はペアごとに異なることに注意してください。つまり、子vへの参照は[v]へのマップに格納でき、対応する子孫のラベルの最初の文字を表示します。 コードを短くし、「すごい、なんてコンパクトなコードだ」と考えるために、構造を記述するオブジェクト指向のアプローチを避けます。 したがって、接尾辞ツリーは次のように表されます（pos、len、および上記の図に注意を払うことができます）。

int sz; //    int pos[0..sz-1], len[0..sz-1], par[0..sz-1]; //par[v] –   v std::map<char, int> to[0..sz-1]; //to[v] –     v
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の重要なプロパティは、サフィックスツリーがO（n）メモリを占有することです。



ルートから頂点vへのパスに書かれた行は、str（v）で示されます。 str（v）は推論にのみ使用され、どこにも明示的に保存されません。

サフィックスツリーの例

サフィックスツリーに慣れると同時に、その使用方法を理解するために、いくつかの例を検討してください。

sの部分文字列を検索します

おそらく最初に思い浮かぶのは、サフィックスツリーを使用して部分文字列を検索することです。 文字列uが文字列sの部分文字列であることに気付くのは非常に簡単です。これは、uが接尾辞ツリーのルートから読み取ることができる場合のみです（一部のiとjに対してu = s [i..j]であり、したがって接尾辞s [i .n-1]はu）で始まります。

文字列sの異なる部分文字列の数

同じ理由で、各部分文字列sが接尾辞ツリーのある辺のラベル上の特定の位置に対応することを確立できます。 したがって、異なる部分文字列の数はそのような位置の数であり、ルートを除くすべての頂点vの合計len [v]に等しくなります。

データ圧縮LZ77

例はもっと複雑です。 LZ77（google Lempel、Ziv）を圧縮するという考え方は簡単で、次の擬似コードで説明できます。

 for (int i = 0; i < n; i = j+1) //  s[0..n-1] if ( s[i]     s[0..i-1]) { j = i,      s[i]; //      } else { j = max{j    d < i ,  s[i..j] = s[d..d+ji]}; d =  0,1,…,i-1 ,  s[d..d+ji] = s[i..j];       (j-i+1, id) //      } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

たとえば、文字列「aababababaaab」は「a（1,1）b（7,2）（3,10）」としてエンコードされます（abababa行の「重複」に注意してください）。 もちろん、実装の詳細は大きく異なる可能性がありますが、基本的な考え方は多くの圧縮アルゴリズムで使用されています。 サフィックスツリーを使用すると、O（n）で同様の方法でsを圧縮できます。 これを行うために、start [v]がs [p..p + | str（v）| -1] = str（v）の最小pと等しくなるように、ツリーの各頂点vをフィールドstart [v]で補完します。 （v）| str（v）の長さです。 葉の場合、この値は簡単に計算できることは明らかです。 残りの頂点については、開始フィールドはツリーの1回の深さによって計算されます。 start [v] = min {start [v ₁ ]、start [v ₂ ]、...、start [v _k ]}、v ₁ 、v ₂ 、...、v _kはvの子です。 ここで、圧縮アルゴリズムでjの次の値を計算するには、ツリーの現在の頂点vが開始する[v] <i;になるまで、ルートから文字列s [i..n-1]を読み取るだけで十分です。 dは、最後のそのような値start [v]に等しいものを選択できます。

サフィックスツリーの構築

単純化されたWeinerアルゴリズムはUkkonenアルゴリズムおよび従来のWeinerアルゴリズムよりも単純であるにもかかわらず、それでもなお非自明でないアルゴリズムであり、それを理解するにはある程度の努力が必要であることを事前に警告します。

一般的な計画。 プレフィックスリンク

アルゴリズムは空のツリーから始まり、サフィックスs [n-1..n-1]、s [n-2..n-1]、...、s [0..n-1]を順番に追加します（念のため、議論中の実装では、extend関数は、サフィックスが最短から始まる長さの昇順で正確に追加された場合にのみ正しく機能すること、つまり、たとえば、コード（for（int i = n-3; i> = 0; i--）extend （i）「バグを含む）：

 for (int i = n-1; i >= 0; i--) extend(i); //    s[i..n-1]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、ループのk番目の繰り返しで、文字列s [n-k + 1..n-1]の接尾辞ツリーがあり、接尾辞s [nk..n-1]がツリーに追加されます。 新しい最長のサフィックスを追加するには、1つの新しいリーフと、場合によっては古いエッジを「分割」する1つの新しい頂点を挿入する必要があることは明らかです。 主な問題は、新しいシートが添付されるツリー内の位置を見つけることです。 この問題を解決するために、サフィックスツリーにプレフィックスリンクが追加されています 。



各頂点vに対して、プレフィックスリンクlink [v]-文字を頂点番号にマッピングするマップを次のように関連付けます。シンボルの場合、リンク[v] [a]は、str（ w）= a str（v）そしてこの場合、リンク[v] [a] = w。 （古典的なWeinerアルゴリズムに精通している場合、プレフィックスリンクは「明示的な」古典的なプレフィックスリンクに対応していることに気づきました。「暗黙的な」リンクはまったく必要ないことがわかりました。Ukkonenアルゴリズムに精通している場合は、プレフィックスリンクは「サフィックスリンク」と逆になります。）図では、プレフィックスリンクは赤で示され、長方形にはリンクに対応するシンボルが含まれています（ダミー頂点0の意味については以下を参照）。





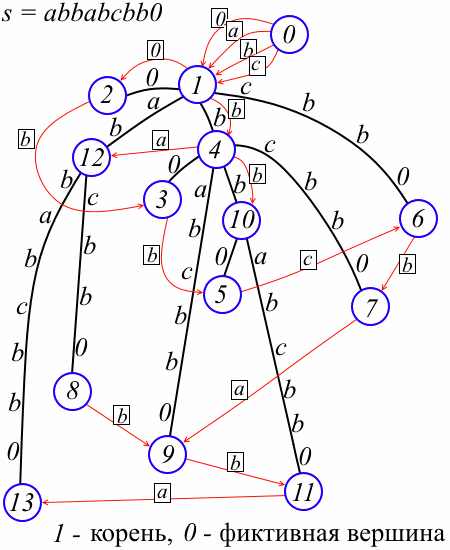
したがって、追加の構造があります。

 std::map<char, int> link[0..sz-1]; // 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

定義により、各頂点につながるプレフィックスリンクは1つだけであるため、リンクはO（n）メモリを占有すると結論付けます。



まず、ここで紹介する実装の技術的なニュアンスについて説明します。 ツリーのルートは頂点1、0はすべての文字aに対してリンク[0] [a] = 1であるようなダミー頂点です。 さらに、par [1] = 0およびlen [1] = 1です。ダミーの頂点には特別なセマンティックロードはありませんが、いくつかの特別なケースを同じ方法で処理できます。 これについては以下で詳しく説明しますが、今のところは注意を払ってはいけません。 新しいサフィックスを挿入するアルゴリズムの説明に進みます。

アルゴリズム

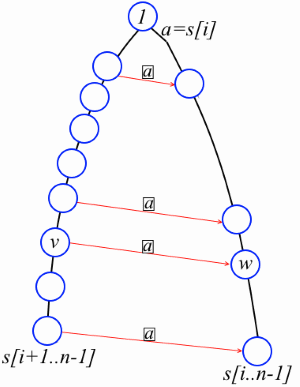補題。 iを0からn-2までの数値とします。 文字列s [k..n-1]のサフィックスツリーを考えます。ここで、k <= iです。 wがs [i..n-1]に対応するルートからリーフへのパス上の非ルート頂点である場合、ルートからs [i + 1..n-1]に対応するリーフへのパス上には、次のような頂点vがあります。 s [i] str（v）= str（w）およびlink [v] [s [i]] = w（図を参照）。



それを証明しましょう。 str（w）= s [i] tを示します。 接尾辞ツリーの定義により、wはリーフであるか、wには少なくとも2つの子孫があります。 wが葉の場合、vは文字列s [i + 1..n-1]に対応する葉です。 wを葉にしないでください。 次に、[w] [a]が1つの子wにつながり、[w] [b]が別の子wにつながるような、いくつかの異なる記号aとbがあります。 s [i] taとs [i] tbはsの部分文字列です（少なくとも1つは位置iで始まりません）。 したがって、taとtbも部分文字列であり、ツリー内にstr（v）= tとなる頂点vが存在する必要があります。 vがs [i + 1..n-1]に対応するシートへのパス上にあり、プレフィックスリンクの定義により、リンク[v] [s [i]] = wであることは明らかです。



したがって、文字列s [i + 1..n-1]のサフィックスツリーがあり、文字列s [i..n-1]のシートを追加し、それに応じてプレフィックスリンクを更新するとします。 下の写真をご覧ください。 s [i + 1..n-1]に対応する古いシートを示します。 新しいシートの「ドッキングポイント」は頂点w 'であり、まだ作成されていない可能性があります。 wによって、w 'のすぐ上にある頂点を示します（wが既にツリーにある場合は、w = w'で、この場合は新しい葉を追加するだけで十分です）。 簡単にするために、最初にwがルートでない場合を考えます。 補題により、リンク[v] [s [i]] = wになるように、古いパスからルートへのパスに頂点vがあります。





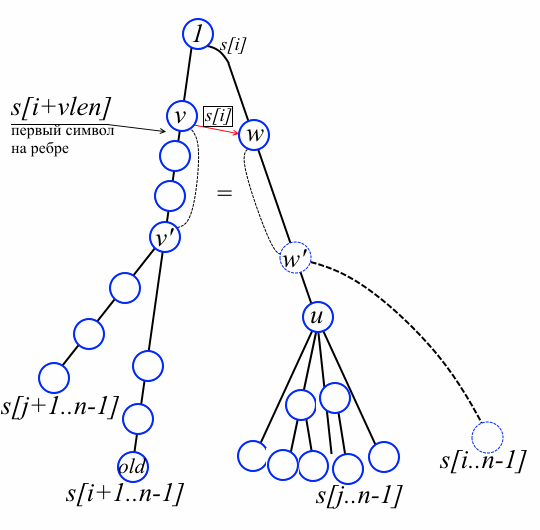
事実1. vからoldへのパスには、v "'リンク[v' '] [s [i]]が定義されているような頂点はありません。 それどころか、v ''がそのようなピークであるとします。 次に、頂点リンク[v ''] [s [i]]はw 'の祖先であり、同時にwの子孫でもあります（プレフィックスリンクの定義による）。 しかし、ドッキングポイントから最も近いピークとしてwを選択しました！ 論争。



アルゴリズムでは、まずvとwを見つけます。 同時に、vlen変数の値| str（v）| +1を計算し、パススタックに渡されたすべての頂点を追加します-それらは引き続き便利です。 サイクルの最後で、s [i + vlen]は、vからoldへのパスの子孫vへのエッジの最初の文字に等しいことに注意してください（上の図を参照）。

  int v, vlen = n - i, old = sz – 1;//   old –    for (v = old; !link[v].count(s[i]); v = par[v]) { vlen -= len[v]; path.push(v); } int w = link[v][s[i]];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

事実2. to [w] [s [i + vlen]]が定義されていない場合に限り、頂点w 'はツリーに既に存在します。 この場合、w = w '。 上の図と、シンボルs [i + vlen]の意味に関する発言を少し黙想すると、このステートメントが明らかになります。



事実3. vから古いパスへのパスには、vがあります。たとえば、wがまだ存在していなくても、s [i] str（v '）= str（w'）です。 w 'ツリーにすでに存在する場合、ステートメントは事実2およびv' = vから明らかです。 wがまだ作成されていないとします。 u = to [w] [s [i + vlen]]を表します。 ルートuを持つサブツリーから任意の葉を選択します。 この葉をjの接尾辞s [j..n-1]に対応させます。 まだ挿入されていない接尾辞s [i..n-1]と接尾辞s [j..n-1]は、「暗黙の」頂点w 'で分岐します。 ただし、s [j + 1..n-1]およびs [i + 1..n-1]に対応するリーフは、ツリーで既に表されており、頂点v 'で分岐しています。 s [i] str（v '）= str（w'）であることは明らかです。つまり、vはvからoldへのパスにあります。 この時点で、上の図を最後に見る価値があります。 アルゴリズムの主要部分に進みます。



wが見つかったので、タスクは新しいシートのドッキングポイントを見つけることです。 実際、len [w ']と頂点v'を探しています。 w = w 'の場合、シートをwにアタッチし、古いシートからこのシートへのプレフィックスリンクを描画するだけで十分です。 w！= W 'の場合の複雑なケース、つまり シンボルs [i + vlen]によるwからのエッジがあります。 再びu = to [w] [s [i + vlen]]を示します。 s [i] str（v '）= str（w'）のような頂点v 'が見つかるまで、パススタックから頂点を順番に取得します。 適切なピークが見つかったことをどのように判断しますか？ v ₁ 、v ₂ 、...、v _kを、v _k = v 'のパススタックの最上部の頂点とします（下図を参照）。 v _pからoldへのパス上の子v _pに続くエッジの最初の文字を_pで示します。 ₀ = s [i + vlen]を定義します。 tをwからuまでのエッジ上のラベルとする。 シンボルt [len [v ₁ ] + len [v ₂ ] + ... + len [v _p -1]]は、t上の_pに対応するシンボルと呼ばれます。 w 'はwからuへのエッジ上の接尾辞s [i..n-1]の分岐点であるため、シンボルa _kは t上の対応するシンボルと等しく_ありません。 一方、同じ理由で、各p = 0,1、...、k-1に対して、シンボルa _pはt上の対応するシンボルと等しくなります。 図面を使用すると、この推論がより明確になります。







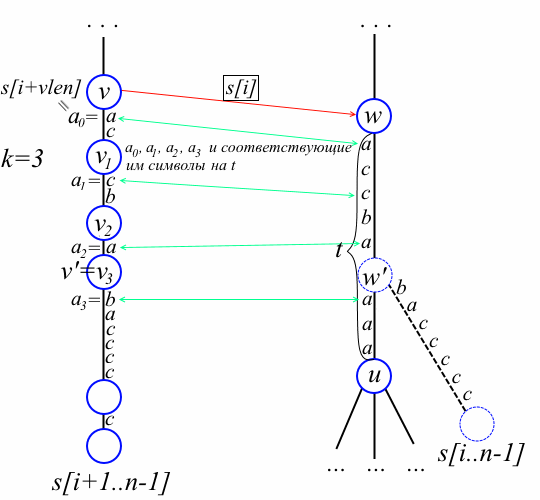
得られた発言は、単純化されたWeinerアルゴリズムの中核です。 興味深いことに、すべての文字ではなく、エッジの最初の文字のみをtの対応する文字と比較すれば十分です。 本質的に、これは簡単な観察です。これはブレスラウアーとイタリアーノが気づいたことですが、何らかの理由で誰も気付いていませんでした。 vからto wへのプレフィックスリンクと古いシートから新しいシートへのプレフィックスリンクを描画することを忘れないでください。 そのため、アルゴリズムは次のように新しいサフィックスs [i..n-1]を挿入します。

  if (to[w].count(s[i + vlen])) { // w != w' int u = to[w][s[i + vlen]]; //sz –    w',    //.. w!=w',  s[pos[u] - len[u]] == s[i + vlen]      for (pos[sz] = pos[u] - len[u]; s[pos[sz]] == s[i + vlen]; pos[sz] += len[v]) { v = path.top(); path.pop(); //   v' vlen += len[v]; }    w  u  w'=sz; len[w'] = len[u]-(pos[u]-pos[sz]) link[v][s[i]] = sz; //   v'  w' w = sz++; // w = w'     } //    w  w' link[old][s[i]] = sz; //   old    sz   sz  w; len[sz] = n – (i + vlen) pos[sz++] = n; //pos     n
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

wがルートである場合、特別なケースを検討する必要があります。 この状況は完全に似ていますが、一部の値は1つシフトされます。 もちろん、このケースを個別に処理することも可能ですが、ダミーの頂点を使用する方が簡単であり、追加のコードを記述する必要はありません。 この場所で重要な役割を果たしているのは、すべての文字aについて、par [1] = 0、len [1] = 1、link [0] [a] = 1です。 したがって、頂点vの検索サイクルは必ず頂点0で終了し、値len [1] = 1は必要なシフトを1つ提供します。 詳細を理解するのは難しくありません。これは演習として残しておきます。 これに関する架空のピークの秘密の意味が明らかにされることを願っています。 すべてを組み合わせることで、次のソリューションが得られます。

 void attach(int child, int parent, char c, int child_len) //  { to[parent][c] = child; len[child] = child_len; par[child] = parent; } void extend(int i) //  ;   i=n-1,n-2,...,0 { int v, vlen = n - i, old = sz - 1; for (v = old; !link[v].count(s[i]); v = par[v]) { vlen -= len[v]; path.push(v); } //   vlen = |str(v)|+1 int w = link[v][s[i]]; if (to[w].count(s[i + vlen])) { // w != w' int u = to[w][s[i + vlen]]; for (pos[sz] = pos[u]-len[u]; s[pos[sz]]==s[i + vlen]; pos[sz] += len[v]) { v = path.top(); path.pop(); //   v' vlen += len[v]; } attach(sz, w, s[pos[u] - len[u]], len[u] - (pos[u] - pos[sz])); // w'(=sz)  w attach(u, sz, s[pos[sz]], pos[u] - pos[sz]); // u  w'(=sz) w = link[v][s[i]] = sz++; //    v'  w';  w = w'     } //    w   w' link[old][s[i]] = sz; //       attach(sz, w, s[i + vlen], n - (i + vlen)); //   sz   w' pos[sz++] = n; //pos     n } void init() { len[1] = 1; pos[1] = -1; par[1] = 0; //,  par[1] = 0  len[1] = 1 (!) for (int c = 0; c < 256; c++) link[0][c] = 1;//  0         }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

アルゴリズムの実行時間の推定

結論として、説明した構造全体がO（n）操作を実行する理由を理解します。 頂点vの高さは、ルートからvまでのパス上の頂点の数です。 アルゴリズムのステップは、ツリーに新しいサフィックスを追加することであることを思い出させてください。 i番目のステップで最も長い接尾辞に対応する頂点_の高さをh _iで示します。 k _iを、ステップiでoldからvに移動した頂点の数とします。 h _iの値はどのように変化しますか？ 補題の図をもう一度見ると、反射時にh _i <h _i-1 -k _i-1 + 2であることがわかります_。i番目のステップで実行される操作の数はk _iに比例します。彼らが気づいたこと、O（h _{i + 1} -h _i + 2）。 このことから、アルゴリズムが合計でO（2n +（h ₁ -h ₂ ）+（h ₂ -h ₃ ）+ ... +（h _n-1 -h _n ））= O（n）操作を実行することは明らかです。



小さな最適化のメモ。 マップへのアクセス時間を考えると、Weinerアルゴリズム（およびUkkonen）の時間はO（n log m）です。ここで、mはストリング内の異なる文字の数です。 アルファベットが非常に小さい場合は、マップの代わりに配列を使用して、Weinerを真に線形にすることをお勧めします。



公平に言うと、簡略化されたWeinerアルゴリズム（および古典的なアルゴリズムなど）がUkkonenよりも約1.5倍から2倍のメモリを消費することは注目に値します。 テストでは、単純化されたWeinerの動作が約1.2倍遅いことも示されました（ここでは、Ukkonenよりわずかに劣っています）。 それにもかかわらず、これらの欠点はすべて、Weinerの実装の容易さと多数の落とし穴の欠如によって部分的に相殺されています。

時系列のリンク

P.ワイナー。 「線形パターンマッチングアルゴリズム」1973は、Weinerの最初の記事で、接尾辞ツリーを紹介し、線形アルゴリズムを示しています。



E.マクレイト。 「スペース節約型サフィックスツリー構築アルゴリズム」1976は、より軽量なサフィックスツリー構築アルゴリズムです。



E.うっこねん。 「接尾辞ツリーのオンライン構築」1995-McCrateアルゴリズムの修正。 最も人気のある最新のアルゴリズム。



D.ブレスラウアー、G。イタリアーノ。 「フリンジマークされた祖先問題によるリアルタイムのサフィックスツリーの構築」2013（2011年の暫定版）-この記事の簡略化されたWeinerアルゴリズムの説明は1段落（10ページの注釈）であり、他のすべては別の関連する問題に当てられています。



PSアルゴリズムのテストとコード改善の提案に協力してくれたMisha RubinchikとOleg Merkuryevに感謝します。



PPS結論として、私は引用します