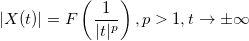、
関数はどこですか
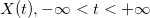条件を満たす：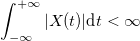 
フーリエ変換
FBDの場合、プロセスを解釈します
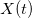一時的なプロセスとして。 関数が特定の周波数を持つコンポーネントの合計である周波数ドメインがあります。 機能 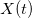として分解することができます 
。
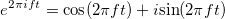成分
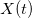頻度で 
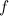形式は次のとおりです。
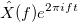どこで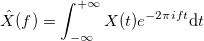 
。
機能
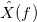フーリエ変換と呼ばれます。
スペクトル密度
初期プロセスの総エネルギーは
。
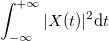プランシュレルの定理により：
。
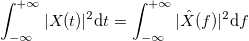平均電力関数
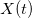セグメント上 
として定義される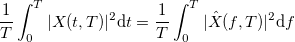 
。
次に、パワースペクトル密度は次のとおりです。
セグメントの長さが無限になる傾向がある場合：
。
なぜなら 機能
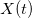次に、 Hurstパラメーターを使用してFWDを説明します 。
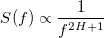
離散フーリエ変換FBD
FBDモデリングのプロセスは、スペクトル密度特性の保存を考慮して、フーリエ級数を使用してフーリエ変換を近似することにより簡素化できます。 その後、逆フーリエ変換を使用して、FWDを取得します。
もし
次に機能する
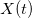実数値。
したがって、以下のアルゴリズムはこの共役対称条件を使用します。
FWD曲線を作成するためのアルゴリズム：
-マット期待値がゼロで、標準偏差が標準の正規分布確率変数。
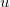-ユニットセグメントに一様分布したランダム変数。
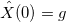
- のために
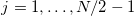フーリエ変換値 
- のために
- 
- それぞれについて
計算： 振幅 （複素数の絶対値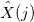 
）、 フェーズ （複素数の引数の値 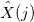、つまり ラジアンで表された角度） - FWB値を計算します。
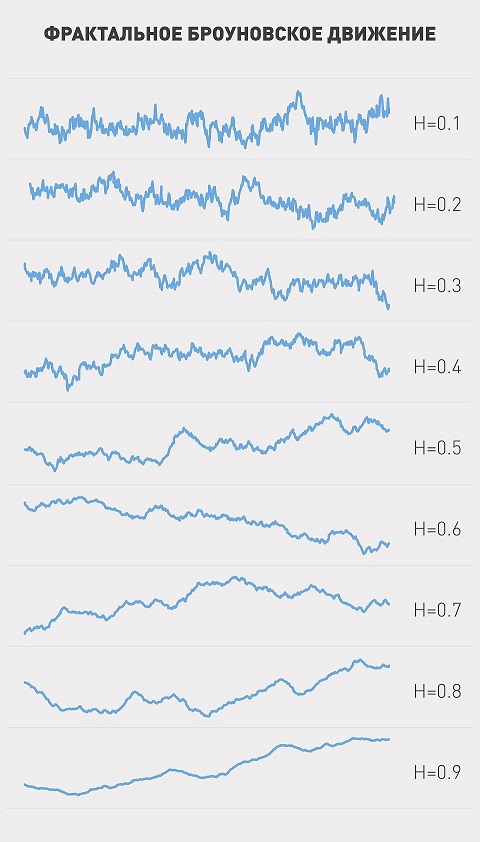
この図は、さまざまなハーストインジケータのFBDのバリエーションを示しています。
FWA生成の使用例
ドルルーブル通貨ペアの最初のシリーズは、期間05/05/2005-05/01/2015に与えられます。
為替レートリターンを計算し、 RS分析を使用して、ドルルーブルペアのハーストインジケーターを見つけます。H= 0.64は、 E（H）= 0.52 x 5.64標準偏差の平均値からはほど遠いです。 Hの値は重要です。 多くの永続的な H> 0.5 、正規化された範囲の変化は時間の平方根よりも速くスケーリングします。プロセスには長期メモリがあります（詳細については、[1]を参照）。
ループがないため、Hurstパラメーターを使用して、フーリエフィルターを使用してフラクタルノイズをモデル化できます。 周波数領域では、スペクトル密度特性を満たすランダムな振幅と位相を持つフラクタルブラウン運動のフーリエ変換を構築します。 逆フーリエ変換を使用して、必要なフラクタルノイズを取得します。
次に、Hurstインデックスが0.64のFWAのさまざまなバリエーションを10,000個生成します。 したがって、為替レートの予測値の分布を取得します。
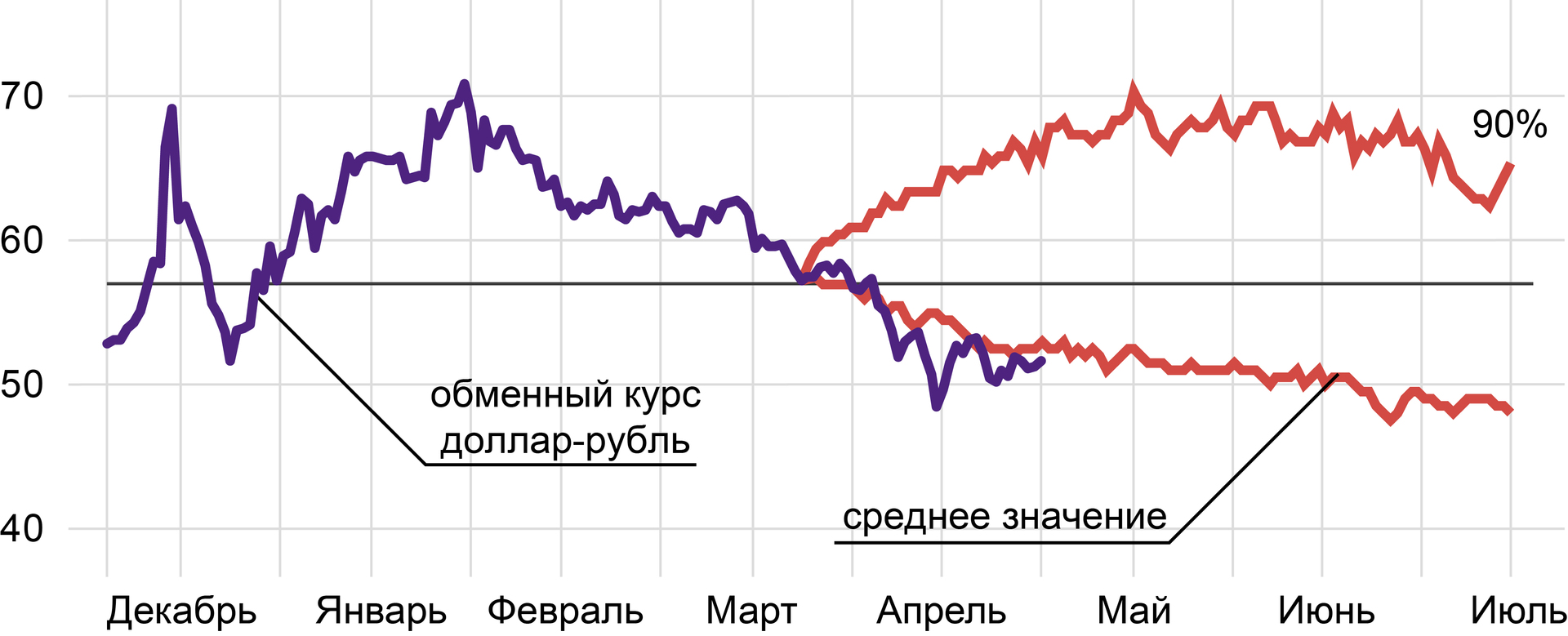
この図は、ドルルーブルの最初の一連の為替レート、および分布の90％の十分位と予測の期待値のグラフを示しています。 1ドルあたりの平均価格は、6月初旬-51.6、7月初旬-52.3ルーブルになります-価格は48.7ルーブルのレベルまで下がります。
参照：
- ゴンチャレンコA.V. USD / RUB通貨ペアのダイナミクスのフラクタル分析//信用機関のリスク管理。 2番（18）。 2015.S. 18-22。