分析、定規、最終-これらの単語は、数学の本当に興味深いセクションが線形代数と呼ばれるものではなく、「降伏して忘れる」というフレーズに関連付けられています。 さまざまな角度から見て、何が良いのか、なぜアプリケーションでこれが非常に役立つのかを見てみましょう。
多くの場合、線形代数の最初の知り合いは次のようになります。
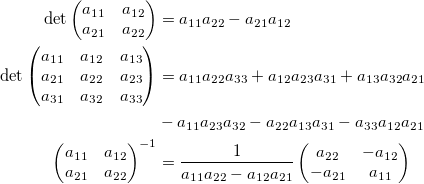
それほど刺激的ではありませんか? すぐに2つの疑問が生じます。これらすべてがどこから来たのか、なぜ必要なのか。
練習から始めましょう。
計算流体力学(CFD)に従事していたとき、同僚の一人が次のように述べました。「私たちは、ナビエ・ストークス方程式を解きません。 行列を描きます。」そして実際、線形代数は計算数学の「主力」です。

この関係を流体力学よりも簡単な例で説明しようとします。
温度がゼロに維持される、両端が固定された細い金属棒を考えてみましょう。 点xの近くでロッドの単位長さあたり毎秒q(x)ジュールを生成する分散熱源を使用して、ロッドを加熱し始めます。 どの温度t = t(x)が確立されますか? モデルの非常に大まかなスケッチを作成しましょう。 平衡が確立されると、ロッドの各セグメント[xh、x + h]に対して 、熱源からの熱流入は、セグメントの境界を通る熱流束の合計に等しくなります。 hが十分に小さい場合、定数まで(これにはhが含まれますが、読者には許されます)、この等式は次のように記述できます。
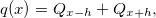
ここで、 Q xhは左の境界を通る熱流束、 Q x + hは右の境界を通る熱流束です。 フーリエの法則によれば、熱流束は温度差に比例します(結局、プールに飛び込むと、最初の数秒で最も寒くなります)。 したがって( hを含む定数まで)

h = 1 / Nとする x i = i・hの形式の点を考えます。ここで、 i = 0、1、2、...、Nです。 それらはグリッドと呼ばれます。 次に、変数t i = t(x i )は方程式を満たします
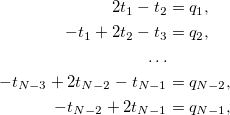
ここで、境界条件をすでに考慮しており、 q i = q(x i )です。 さて、一次方程式系ができました:
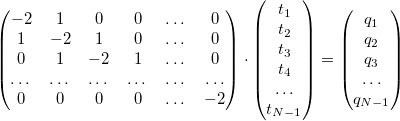
具体的には、このシステムはいわゆるスイープ法によって「正面から」解決できますが、実際のモデルではシステムはより複雑になります。 ここで線形代数が助けになります。
- システムを短い形式A・y = bで記述します(これが行列乗算の起源です!)。
- 解決策があるかどうか、そしてそれが一意であるかどうかを理解する。
- (この例では) Aが数値であるかのように、単純な式y = A -1 bを使用して検索します。
- (計算数学に流れ込む)線形方程式系を解くための効果的な数値手法を構築します。
そして、これは数学的モデリングの観点からの線形代数の単なる見方です。 また、量子力学、統計などがあります。
別の例として、1つのサイト(またはインターネット一般) のページのリンクランキングのよく知られている問題を引用します 。
Nページがあり、それぞれに他のページへのリンクが含まれている場合があります。 どのページが最も重要かを判断する必要があります。 「重要性」を正確に測定する方法は、タスクの一部です。 非負の数(重み)として定量的に提示します。 自然な仮定から始めましょう。このページへのリンクが多いほど、重みが大きくなります。 このアプローチには次の欠点があります。リンクページの重みを考慮していません。 重みのあるページからのリンクには、より多くの意味があるはずです。 これらの考慮事項はこのモデルに私達を導きます:
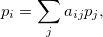
ここで、a ijはi番目のページへのリンクの数で、 j番目をj番目のページからのリンクの総数で割ったものです。 この式は次のように読むことができます。i番目のページの重みは、 j番目のページの重みとj番目のページからi番目のページへのリンクの割合による積の合計に等しくなります。 したがって、問題を線形方程式系に限定しました。 さらに、重みベクトルpは、固有値1に対応する行列Aの固有ベクトルです。
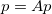
このベクトルの存在(厳密に言えば、わずかに変更された行列Aの場合 )は、フロベニウス-ペロンの定理によって保証されます。 そして、単純な繰り返しで見つけることができます。
したがって、線形代数は、さまざまな分野に適用できる非常に普遍的なアイデアとツールのセットです。 しかし、ネズミ捕りのチーズだけが無料であり、普遍性にお金を払わなければなりません:いくつかの定義と定理は、不必要に抽象的で混乱しているように見えるかもしれません。 しかし、これはそうではありません。実際、多くの抽象化は、人生を複雑にするのではなく、簡素化するように設計されています。 「アヒルのように見え、アヒルのように泳ぎ、アヒルのように鳴くなら、これはおそらくアヒルです」 -実際には抽象化であり、慣れれば非常に便利です。 線形代数と同じこと。 この点をもう少し具体的に説明するために、「外部検査」を補完して、内部の内容について簡単に説明します。
今少し理論
線形代数は、ベクトル空間と、あるベクトル空間を別のベクトル空間にマッピングする関数を研究します。 主に線形関数を考慮します(任意の数値αおよびβおよび任意のベクトルxおよびy に対してf(α・x +β・y)=α・f(x)+β・f(y)の関係を満たす )。 非線形(たとえば、2次形式)もあります。 しかし、最初に、ベクトル(およびベクトル空間)とは何かを理解する必要があります。 そして、これは見かけほど簡単ではありません。
教科書とコースは通常、8ポイントの抽象的な定義を提供します。 また、ベクトル空間は、スカラーによる乗算が定義され、4つの公理を満たす加算的に記述されたアーベル群であるとも言われます。 しかし、線形代数を最初に研究している人にとって、これはそれを理解するのに役立つ可能性が低いです。 いくつかの特定の例を見て、それらの類似性を確認する方がはるかに簡単です。 そして、8点の定義は、この類推の形式化にすぎません。 したがって、すぐに例に進みます。
もちろん、学校の誰もが知っている方向性のあるセグメントはベクトルです。 多くの有向セグメントは、ベクトル空間の例です。 次に、多項式について考えます。 それらを一緒に追加し、数字を掛けることができます。 注意:代数の観点から、多項式を追加し、多項式に数値を乗算するこれらの操作は、有向セグメントの場合と同じルールに従って正確に機能します。 たとえば、等式x + y = y + x (可換性)は、有向セグメントと多項式の両方に当てはまります。 したがって、多項式のセットはベクトル空間であり、多項式はベクトルです。
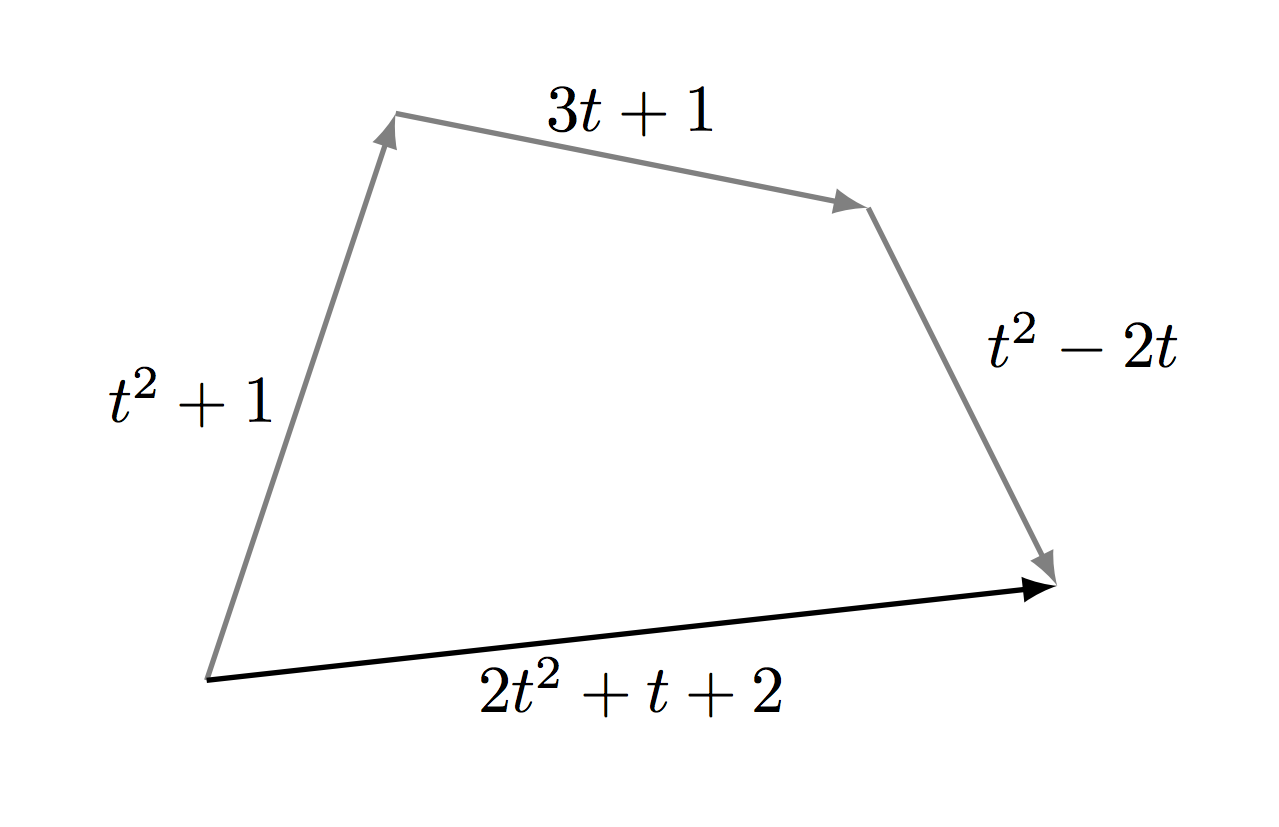
多項式は有向セグメントに似ているため、座標も必要です。 しかし、それらを探す方法と、多項式にはいくつの座標がありますか? 誰もが知っているように、平面上では各ベクトルは正確に2つの座標を持ち、空間では3つです。 これはなぜですか? そして、一般的に次元とは何ですか? 線形代数は、この質問に対する答えを提供します。次元は、線形独立ベクトルの最大数です。 線形独立とはどういう意味ですか? ベクトルx 1 、x 2 、...、x nは、少なくとも1つが非ゼロである数α1、α2、...、αnがある場合、線形従属と呼ばれます。
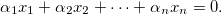
ベクトルが線形に依存しない場合、線形独立と呼ばれます。 (線形依存の概念は、平行および共面ベクトルの概念を一般化します。2つのベクトルは、平行である場合にのみ線形に依存します。3つのベクトルは、共面である場合にのみ線形に依存します。)
空間の次元は、有限( N以下の次数の多項式の空間)と無限(すべての多項式の空間)のいずれかです。 どちらの場合も実際には発生しますが、有限次元に限定しましょう。 ベクトルx 1 、x 2 、...、x nを線形独立、 nを空間の次元とします。 その後、他のベクトルxは、線形結合x 1 、x 2 、...、x nとして、独自の方法で記述できます。 対応する線形結合の係数は座標と呼ばれます。
これで、座標の厳密な定義ができました。 しかし、ポイントはこれだけではありません。途中で、線形結合と線形依存性のより基本的な(そしてあまり目立たない)概念に出会いました。 また、 n次元の線形空間では、 n個の線形独立ベクトルしか存在できないこともわかりました。 この事実は、線形代数の基礎の1つです。
少なくともこれから利益を得るにはあまりにも少ないと思われるように思われます。 しかし、今では一見線形代数に関係しない問題を解決できます。 たとえば、次のとおりです。与えられた多項式pおよびq ; 2つの変数R = R(x、y)に 、すべてのtに対してR(p(t)、q(t))= 0となるような多項式が存在しますか?
一方、「テストラン」は終了します。 しかし、線形代数を研究するさまざまな方法を簡単に議論することは残っています。 ここでは、自分自身の経験の短いレビューに限定し、それに基づいていくつかのヒントを提供しようとします。
ウィキペディアの本-知識のベストソース
線形代数の私の知り合いは、O.V。の本の独立した研究から始まりました。 マンツロバとN.M. Matveeva学校にいたときの「高等数学のコース」。 この本は、この分野の最高の(最悪ではない)知識源からはほど遠いものです。 私の手に渡った高等数学の最初の教科書になったばかりで、その内容は学校のカリキュラムよりも興味深いように思えました。 自信を持って言えるようになりました:学生が最初に勉強する必要のある(そして、それほど面白くない)他の本がたくさんあります。 たとえば、「非標準の問題を解決する方法」(Kanel-Belov A.Ya.、Kovaldzhi A.K.)または「Leningrad数学的円」(Genkin S.A.、Itenberg I.V.、Fomin D.V.)。 本から線形代数を勉強することを引き受ける場合、我慢してください:それは望ましい結果を達成するように見えるよりも時間がかかるかもしれません。
私はまだ線形代数(および数学の他の多くの分野)の基本的な知識をL.Iに負っています。 モスクワ物理技術研究所の伝説的な教師であるコバレンコは、セミナーや相談で常に満員でした。 彼女が各学生に払った注意を過大評価して、課題やいわゆる「カード」(個々のタスク)を夜遅くまで受け入れることは困難です。 そして、これらの降伏の間、私たちはお互いに積極的にコミュニケーションを取りました。 これらすべてにより、教科書に書かれていることだけでなく、そこにないもの、つまり直観やトリックなどを素早く習得することができました。
生徒と教師(およびお互い)のライブコミュニケーションは何も置き換えることはできません。これは従来のコースの利点です。 しかし、私自身がアシスタントとして働いてセミナーをリードしたとき、有意義なコミュニケーションのためにより多くの時間が残されるように、いくつかのものを自動化したいという要望がしばしばありました。 生徒は、標準的な質問に対する標準的な回答を得るために、教師との会議を待つ必要がありますか? または、そのような標準的なタスクが正しく解決されるかどうかを調べますか? ただし、生徒を過小評価しないでください。ほとんどの場合、生徒は「ほとんど意味のない仕事」をしているときに気分が良くなり、これも生徒をやる気にさせます。 証明または解法の確認は1つのことですが、たとえば、線形方程式の解の確認はほぼ完全にコンピューターに委ねることができます。 さらに、多くの場合、答えの検証だけでなく、解自体の一部、たとえば基本行列変換も自動化することができます。
だから
- 線形代数のアイデアと方法は、興味深い問題を解決する際に理解するのが最も簡単です(他の領域からのものを含む:これは抽象的な概念をよりよく理解するのに役立ちます)。
- これを単独で行うのではなく、友人や優れた教師と一緒に行うのが最善です(さまざまなフォーラムがまだ非常に便利です)。
- 日常的な行動が動機付けになる場合は、オンラインコースやその他の自動化方法を使用します(ここでは比例感が必要です。たとえば、行列をWolfram Alphaに変換する前に、ペンと紙でこれを行うことを学ぶ必要があります)。
- 本はあなたがより深く動くことを可能にしますが、時間を追跡することを忘れないでください。
- 線形代数の基本概念と定理はゼロからは現れませんでした。 動機、内部ロジックを理解し、対象の直感的なビジョンを開発するために努力することは有用です。 実際、Kramer、Gauss、Peano、および他の多くの人々は、これらの基礎を(まずは自分自身で)発見することに確実に興味を持っていました。 なぜ線形代数を研究している人々はこれで退屈するのでしょうか?