Clever Geek Handbook

高速階乗アルゴリズム

階乗の概念はすべての人に知られています。 これは、1からNまでの連続した自然数の積を計算する関数です：N！ = 1 * 2 * 3 * ... *N。階乗は急速に成長する関数であり、Nの値が小さい場合は値N！ 多くの重要な数字があります。



この関数をプログラミング言語で実装してみましょう。 明らかに、長い算術をサポートする言語が必要です。 私はC＃を使用しますが、同じ成功を収めれば、JavaまたはPythonを使用できます。



素朴なアルゴリズム



そのため、最も単純な実装（素朴と呼びましょう）は、階乗の定義から直接取得されます。 



static BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; }


私のマシンでは、この実装はN = 50,000の場合に約1.6秒間機能します。



次に、単純な実装よりはるかに高速に動作するアルゴリズムを検討します。



ツリー計算アルゴリズム



最初のアルゴリズムは、長さがほぼ同じである長い数字が短い数字で乗算されるよりも効率的に乗算されるという考慮事項に基づいています（単純な実装のように）。 つまり、階乗を計算するときに、因子が常にほぼ同じ長さになるようにする必要があります。



LからRまでの連続した数の積を見つける必要があるとすると、P（L、R）としてそれを示します。 LからRまでの間隔を半分に分け、P（L、R）* P（M + 1、R）としてP（L、R）を計算します。ここで、MはLとRの中間にあり、M =（L + R）/ 2 。係数はほぼ同じ長さになります。 同様にP（L、M）とP（M + 1、R）を分割します。 各間隔に2つ以下の要素が残るまで、この操作を実行します。 明らかに、LとRが等しい場合、P（L、R）= Lであり、LとRが1つ異なる場合、P（L、R）= L * Rです。 Nを見つけるには！ P（2、N）を数える必要があります。



N = 10に対してアルゴリズムがどのように機能するかを見てみましょう。P（2、10）を見つけます。



P（2、10）

P（2、6）* P（7、10）

（P（2、4）* P（5、6））*（P（7、8）* P（9、10））

（（P（2、3）* P（4））* P（5、6））*（P（7、8）* P（9、10））

（（（2 * 3）*（4））*（5 * 6））*（（7 * 8）*（9 * 10））

（（6 * 4）* 30）*（56 * 90）

（24 * 30）*（5 040）

720 * 5,040

3 628 800



因子がノードにあり、結果がルートで取得される一種のツリーが判明します

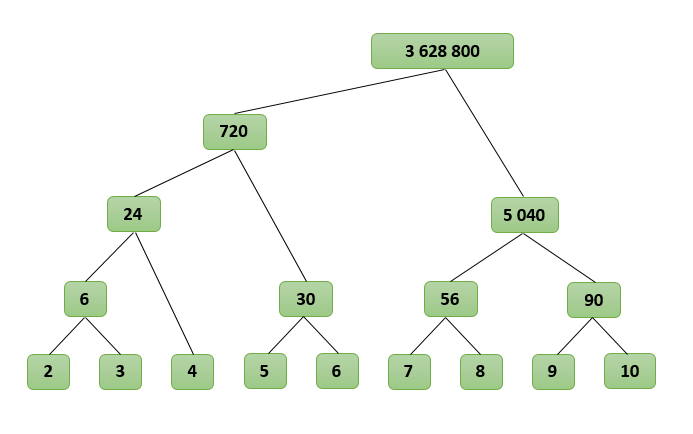
階乗計算ツリー



説明したアルゴリズムを実装します。 



 static BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } static BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); }


N = 50,000の場合、階乗は0.9秒で計算されます。これは、単純な実装のほぼ2倍の速度です。



因数分解計算アルゴリズム



2番目の高速計算アルゴリズムは、素因数分解（因数分解）を使用します。 明らかに、分解N！ 2からNまでの素因数のみが関係しているので、素因数KがNに含まれる回数を計算してみましょう、つまり、展開における因数Kの次数を調べてみましょう。 積の各K番目の項1 * 2 * 3 * ... * Nはインデックスを1つ増やします。つまり、指数はN / Kに等しくなります。しかし、Kの各第2項は次数をもう1つ増やします。つまり、インデックスはN / Kになります。 + N / K 2 。 K 3 、K 4などについても同様です。 その結果、単純な係数Kの指数はN / K + N / K 2 + N / K 3 + N / K 4 + ...



明確にするために、デュースが10に含まれる回数を計算します！ 2番目の係数（2、4、6、8、および10）は、すべてのそのような係数10/2 = 5のデュースを与えます。4番目ごとは、そのようなすべての係数10/4 = 2（4および8）の4（2 2 ）を与えます。 8分の1ごとに8の数字（2 3 ）が得られます。このような係数は1つの10/8 = 1（8）だけです。 16（2 4 ）以上は単一の要因を与えません。つまり、計算を完了することができます。 まとめると、10の拡張でデュースの指数が得られます！ 単純な係数では、10/2 + 10/4 + 10/8 = 5 + 2 + 1 = 8に等しくなります。



同じように行動すると、展開10の3、5、および7のインジケーターを見つけることができます。その後、製品の値を計算するためだけに残ります。



10！ = 2 8 * 3 4 * 5 2 * 7 1 = 3 628800



2からNまでの素数を見つけることは残っています。このためには、 エラトステネスのふるいを使用できます。 



 static BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; //     List<Tuple<int, int>> p = new List<Tuple<int, int>>(); //      for (int i = 2; i <= n; ++i) if (!u[i]) //  i -    { //      int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } //       p.Add(new Tuple<int, int>(i, c)); //      int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } //   BigInteger r = 1; for (int i = p.Count() - 1; i >= 0; --i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; }


この実装では、50,000を計算するのに約0.9秒かかります！



GMPライブラリ



正しく書かれているように、階乗計算率は乗算率に依存して98％です。 GMPライブラリを使用してC ++で実装して、アルゴリズムをテストしてみましょう。 テスト結果を以下に示します。C＃の乗算アルゴリズムにはかなり奇妙な漸近現象があるため、最適化ではC＃のゲインが比較的小さく、G ++を使用したC ++のゲインが大きくなります。 ただし、この問題はおそらく別の記事の価値があります。



性能比較



すべてのアルゴリズムは、10回の反復で1,000、2,000、5,000、10,000、20,000、50,000、および100,000に等しいNについてテストされました。 この表は、ミリ秒単位の平均稼働時間を示しています。

結果表



折れ線グラフ

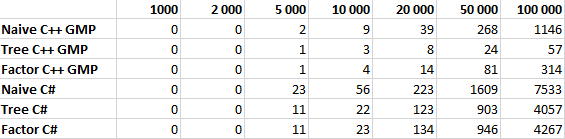
折れ線グラフ



対数グラフ

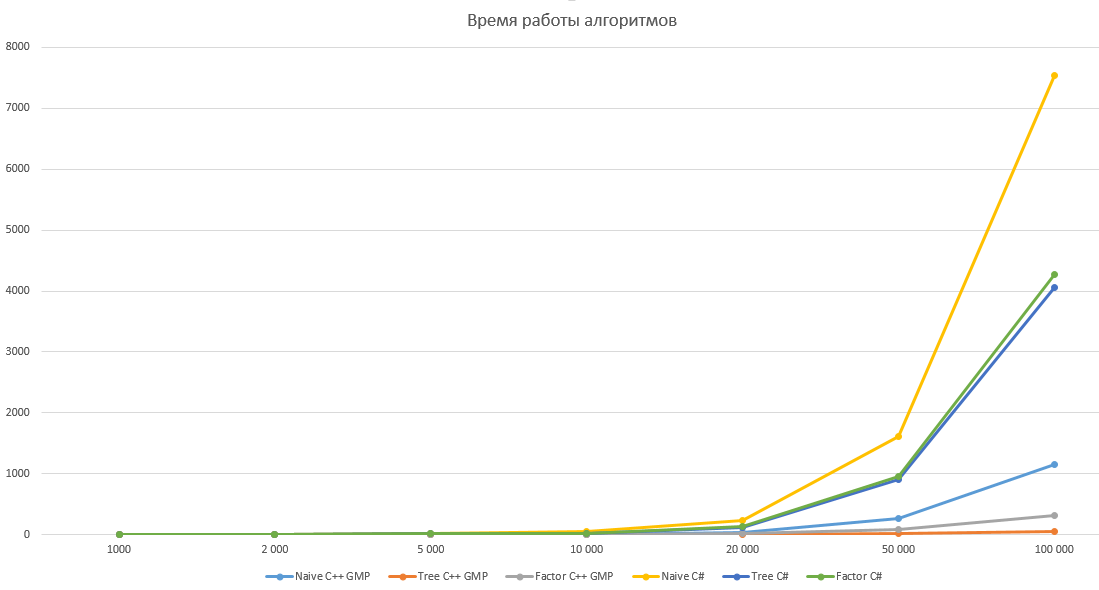
対数グラフ



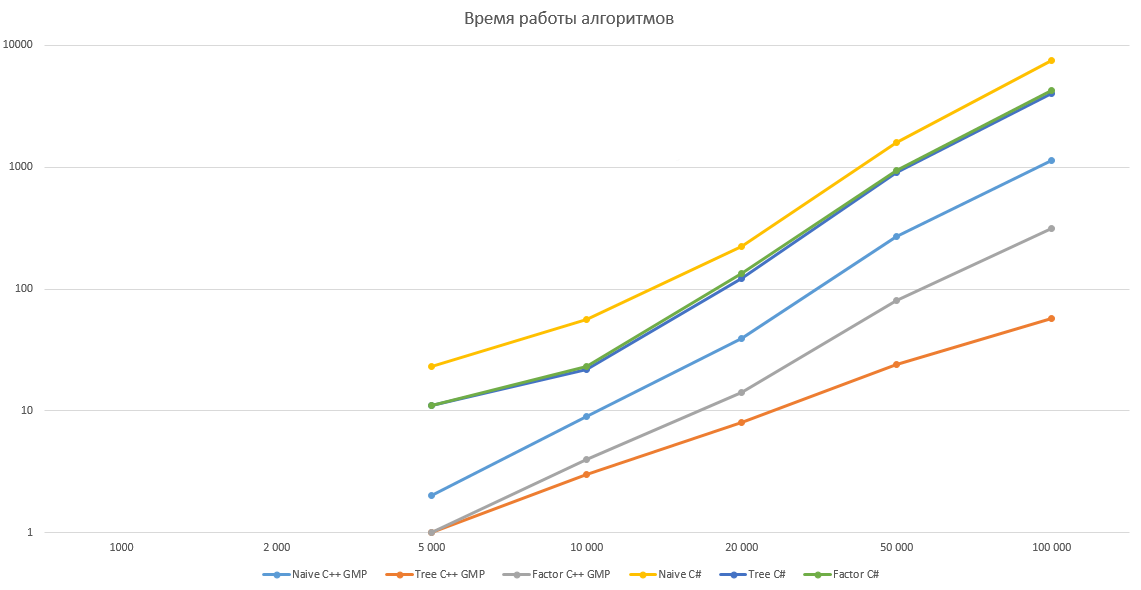
コメントからのアイデアとアルゴリズム



ホーカーは私の記事に応えて多くの興味深いアイデアとアルゴリズムを提供しました。ここではそれらのベストへのリンクを残します



Stream APIを使用してJavaでツリーを並列化し、18倍の高速化を実現

Mrrl は15-20％の因数分解の最適化を提案しました

PsyHaSTe は、素朴な実装の改善を提案しました

Krypt はC＃の並列バージョンを提案しました

SemenovVV はGoでの実装を提案しました

GMPを使用することをお勧めします

ShashkovS はPythonの高速アルゴリズムを提案しました



ソースコード



実装されたアルゴリズムのソースコードは、ネタバレの下に記載されています。

C＃ 
 using System; using System.Linq; using System.Text; using System.Numerics; using System.Collections.Generic; using System.Collections.Specialized; namespace BigInt { class Program { static BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } static BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } static BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } static BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; List<Tuple<int, int>> p = new List<Tuple<int, int>>(); for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.Add(new Tuple<int, int>(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } BigInteger r = 1; for (int i = p.Count() - 1; i >= 0; --i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; } static void Main(string[] args) { int n; int t; Console.Write("n = "); n = Convert.ToInt32(Console.ReadLine()); t = Environment.TickCount; BigInteger fn = FactNaive(n); Console.WriteLine("Naive time: {0} ms", Environment.TickCount - t); t = Environment.TickCount; BigInteger ft = FactTree(n); Console.WriteLine("Tree time: {0} ms", Environment.TickCount - t); t = Environment.TickCount; BigInteger ff = FactFactor(n); Console.WriteLine("Factor time: {0} ms", Environment.TickCount - t); Console.WriteLine("Check: {0}", fn == ft && ft == ff ? "ok" : "fail"); } } }
GMPを使用したC ++ 
 #include <iostream> #include <ctime> #include <vector> #include <utility> #include <gmpxx.h> using namespace std; mpz_class FactNaive(int n) { mpz_class r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } mpz_class ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (mpz_class)r * l; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } mpz_class FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } mpz_class FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; vector<bool> u(n + 1, false); vector<pair<int, int> > p; for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.push_back(make_pair(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } mpz_class r = 1; for (int i = p.size() - 1; i >= 0; --i) { mpz_class w; mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second); r *= w; } return r; } mpz_class FactNative(int n) { mpz_class r; mpz_fac_ui(r.get_mpz_t(), n); return r; } int main() { int n; unsigned int t; cout << "n = "; cin >> n; t = clock(); mpz_class fn = FactNaive(n); cout << "Naive: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class ft = FactTree(n); cout << "Tree: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class ff = FactFactor(n); cout << "Factor: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class fz = FactNative(n); cout << "Native: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; cout << "Check: " << (fn == ft && ft == ff && ff == fz ? "ok" : "fail") << endl; return 0; }




More articles:


All Articles