ランダム変数yが何か(たとえば、時間または別のランダム変数x)に線形に依存していることがわかっている場合、つまり 法律y(x)= Ax + bに従って、線形回帰が使用されます(したがって、前回の記事では、登録数のビュー数への依存性を構築しました)。 線形回帰の場合、係数Aおよびbは、既知の式を使用して計算されます。 未知のパラメーターを決定するために、指数などの別のタイプの回帰の場合、対応する最適化問題を解く必要があります。つまり、最小二乗法(LSM)内で、最小二乗和(y(x i )-y i ) 2を見つける問題。
そのため、ここで例として使用するデータを示します。 出席者のピーク(多数のビュー、赤い点線)は、記事の公開時に発生します。 データの2行目(Regs、係数100)は、読み取り後に特定のアクションを実行したリーダーの数を示します(Mathcad Expressの登録とダウンロード-ちなみに、この記事と以前の記事のすべての計算を繰り返すことができます)。 すべての写真はMathcad Expressのスクリーンショットであり、 ここで計算してファイルを取得できます 。

グラフ上の緑色の矢印を使用して、非線形回帰を作成するデータを指定しました。 私たちが基礎とするモデルによれば、出版物の出版後の短い移行期間の後、ビューの数はほぼ指数法則に従って時間とともに減少します。
ビュー≈C 0 ∙exp(C 1 ∙t)。
このモデルの正当化は、ポアソンランダムプロセスに関しては、将来の記事の1つまで延期されます。
分析のために、モデルに対応するフラグメントを選択する必要があることは明らかです(最初のピークに近すぎ、2番目の記事の後の訪問の統計と合計しません)。 最初のチャートの緑の矢印で強調されているのはこのギャップであり、より大きなスケールでは次のようになります。

指数回帰は、このような指数関数のグラフを決定することを思い出します。これは、示された実験点に最も近い「平均」になります。 回帰係数を見つけるには、目的関数の最小値を見つける最適化問題を解決する必要があります。
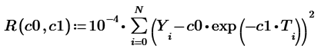
(T、Y)はN個の実験点の配列です。便宜上、この係数を導入しました(最小値の位置には影響しません)。 さらに、必要なC0とC1を取得するために、組み込みの最小検索関数を使用して1行または2行のコードをすぐに書くこともできますが、無料のMathcad Expressを使用してすべてオフにしますので、もう少し面倒になります(ただし、理解しやすいおよび視覚的)方法。
まず、関数R(c0、c1)の動作を見てみましょう。 これを行うために、c0のいくつかの値を修正し、それぞれに対して1つの変数R(c0、x)の関数のグラフを作成します。
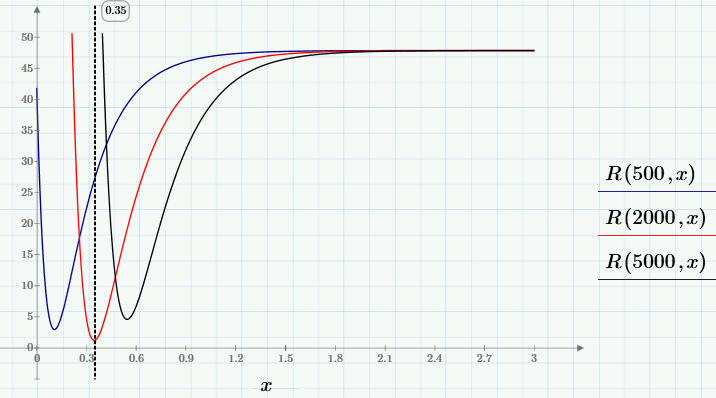
選択されたc0に対して、ファミリ内のグラフのいずれかに最小値が1つあり、その位置xはc0に依存していることがわかります。 x = g(c0)と書くことができます。 最も深い最小値、つまりR(c0、g(c0))〜minの最小値は、望ましいグローバルな最小値になります。 問題を解決するために彼を見つける必要があります。 グローバルな最小値を見つけるには、まず(Mathcad Expressで使用可能なツールを使用して)ユーザー定義関数g(y)を定義し、次に最小R(y、g(y))を見つけます。
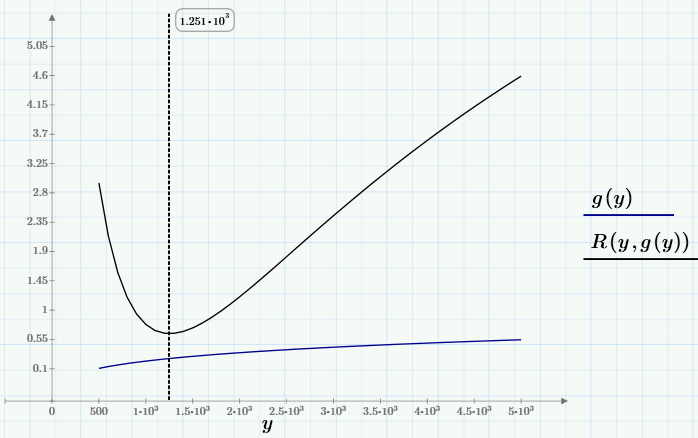
最小値を計算するための数値アルゴリズムについては触れません(興味がある人は、次のスクリーンショットの最初の行に表示されています)。 問題の解決策(ポイント、選択した表記c0 = y0およびc1 = x0)、このポイントでの目的関数の値、および回帰グラフを以下に示します。
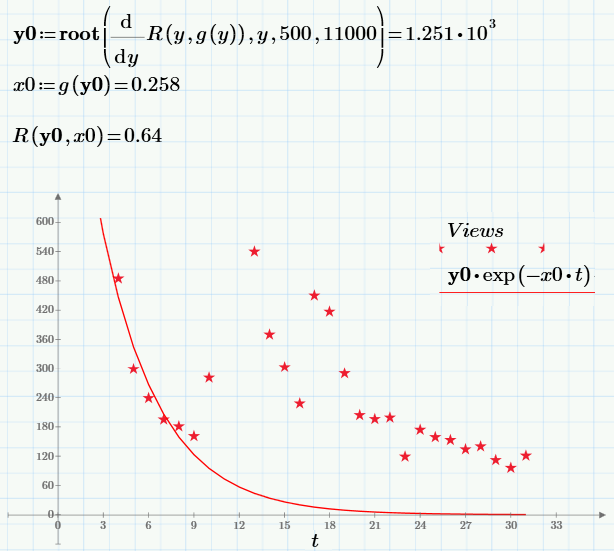
結果に満足できますか? 最も可能性が高いのは、構築された回帰が実験ポイントにあまり適合しないためです。 回帰(指数が急速にほぼゼロに低下する)とデータ(見ることができるように、かなりの時間が経過した後でも、ビューの数はゼロではないが約100)で大きく異なる「テール」。
したがって、結果を改善するために、モデルを改善しましょう。 記事が表示される回数のモデルは、2つのチャネルを経由する訪問の合計であると想定しています。
- ポアソン統計ビューのチャネル≈0∙exp(1∙t);
- ビューの数がほぼ一定のチャネル(パラメータc2と呼びましょう)。
この3番目のパラメーターc2は、過去10日間のビューの平均値と同様に、実際にポアソン訪問者が存在しない場合のデータの「テール」の分析から決定できます。
最後に、c2を知って、フォームの改善された回帰を構築できます。
ビュー≈0∙exp(1∙t)+2
上記のアルゴリズムを完全に繰り返します。
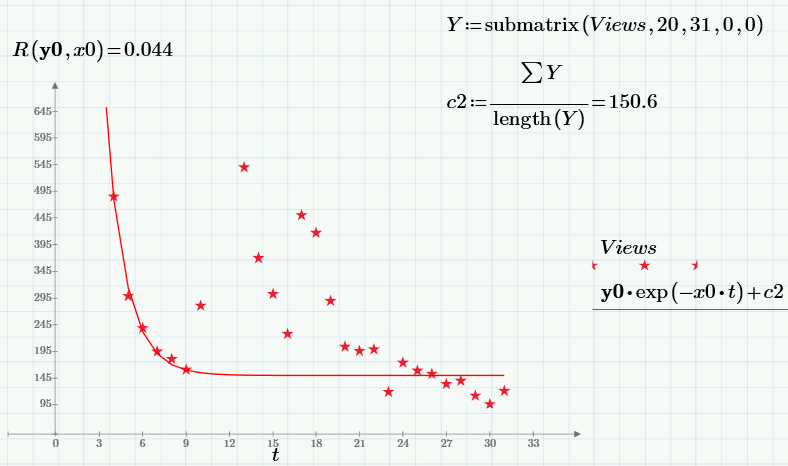
最小の目的関数の値(つまり、残差の2乗の合計)は、c2 = 0の場合と比べて1桁以上減少することに注意してください!
結論として、指数回帰を見つけるための組み込みexpfit関数の結果を提供します(Mathcad Primeの商用バージョンで利用可能)。 作業の結果は緑の点線でグラフに表示され、結果(前のグラフと同じ)は赤の実線で表示されます。
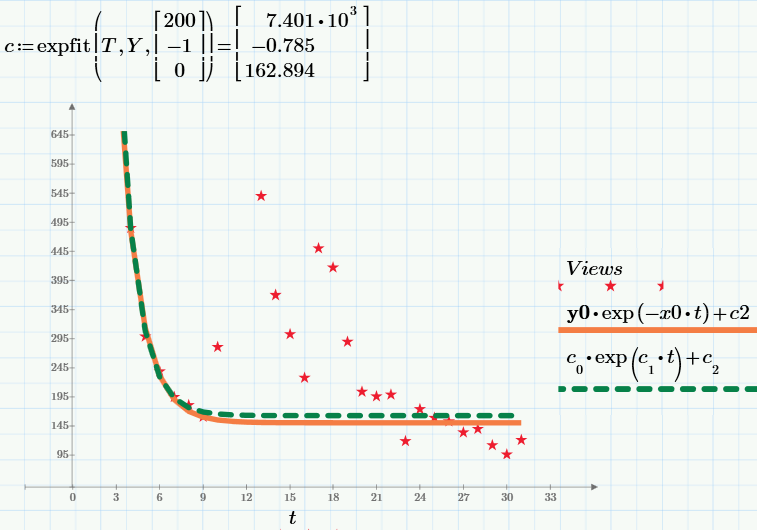
すべての写真はMathcad Expressのスクリーンショットです(計算自体はここで取得し、繰り返し、必要に応じて変更して使用できます)。 計算の最初にc2 = 0またはc2 = 150を設定して、それぞれ最初または2番目のモデルを選択することを忘れないでください。