量子サンドボックス：パート1
量子状態とは何ですか？ 通常の状態は量子状態とどう違うのですか？ 通常の状態はどの時点で量子になり、量子状態を削除するとどうなりますか？ それはまだ量子的ですか、それとも普通に変わりますか？ それは単なる量子でした。 それは混乱したに違いない、そして猫も混乱した。
この記事では、これらの質問に答え、量子力学の本質を理解しようとします。
目的：量子進化を模倣した簡単なプログラムを作成して、最終的にこれらの量子ビットをペンで感じることができるようにします。
目次：
- パートI：クラシック状態
- パートII：量子状態
- パートIII：猫
- パートIV：ロイ
通常の「状態」とは何ですか？ この用語は頻繁に使用されるため、完全に直感的に認識されるようになりました。
パートI：クラシック状態
質問1： 「セグメントに沿って観察できる特定の粒子P。 粒子Pの状態は何ですか？」
回答： 粒子P の 古典的な状態は、セグメントからの数です。
注意深い読者は「観察する」という言葉に魅了されます。これをどのように理解しますか？
今回はサイト上で
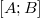「監視する」何らかの「検出器」がありましたが、なぜそれらについて何も言わなかったのですか？ そして、何個ありますか？
パーティクルの状態はセグメントからの数であると言った
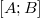。 パワーセット 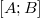連続体に等しい-「境界線」AとBの間には無限に多くの数があり、それらは互いに無限に近くに位置しています-それは、各ポイントに無限に多くの検出器が必要であることを意味しますか？ かなり高価ですね。
しかし、その状態は数字であると主張すると、まさにそれを意味することがわかります。 まさに、私たちが無限に多くの検出器を持っているという事実です。 しかし、これはそうではありません。 そして、これは原則的にできません。
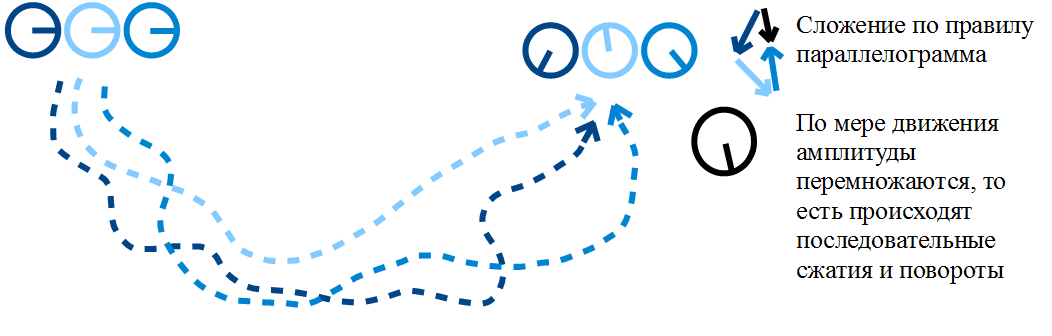
実際には、セグメントを有限数のセグメントに分割し、交差点に検出器を配置します。各検出器は、その近傍に粒子があるかどうかをほぼ知ることができます。
上記で行われたことを量子化と呼びます。 この場合、セグメントをセグメントに量子化しました。 量子は、使用されるモデルのフレームワーク内の何かの不可分な部分、抽象的な用語です。
最も興味深い現象は、粒子の状態がもはや単なる数値ではなくなったために正確に始まります。
パートII：量子状態
質問番号2： 「与えられた粒子P。間隔内の特定の数の検出器の近くでのみ観測できます。
回答： ???
例を考えてみましょう：
ダンカット
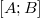そして、ポイントAとBにある2つの検出器。
各検出器には、粒子がこの検出器からどれだけ離れているかを判断できる特定の数値が表示されます。
Aは最初の検出器です。
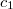-彼の証言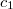（ = 1、パーティクルがAに直接送られた場合
Bは2番目の検出器です。
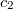-彼の証言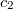（ =粒子がBで直接ヒットした場合1
私たちの研究の範囲を何らかの形で制限するために、粒子の仮定を提示しましょう。
仮定： パーティクル は 1つだけで、それ自体を取得して複製することはできません。
この仮定から、粒子がAにある場合、Bにあることはできず、その逆も成り立ちます。
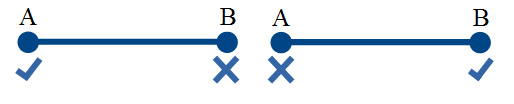
または、何が同じ場合
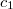= 1その後 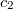= 0およびその逆。
ここで、検出器Aから検出器Bへの粒子の「移動」を考えます。粒子はA（
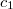= 1 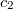= 0）、その後、Bに向かって飛行し始めました。検出器Aの読み取り値が減少し始めました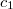（ <1）、検出器Bの読み取り値が増加し始めた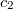（ > 0）。 その後、粒子は検出器Bに到達し、その読み取り値は等しくなります 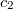= 1、検出器Aは粒子が存在しないことを通知します 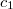= 0。
したがって、検出器自体とその読み取り値を使用して、粒子の状態を説明します。
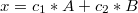
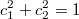
このレコードは、構成Xに番号c1を示す検出器Aと番号c2を示す検出器Bが含まれることを意味します。
質問2： 「与えられた粒子P。これは、セグメントの量子化であるポイントAおよびBにある検出器の近くでのみ観察できます。
仮定： パーティクル は 1つだけで あり 、それ自体をクローン化することはできません。
回答： 粒子P の 量子状態は、2次元ヒルベルト空間のベクトルです
質問2（一般化）： 「与えられた粒子P。これは、点に位置する有限数の検出器の近くでのみ観察できます。N-1セグメント上のセグメントの量子化
。 粒子Pの状態は何ですか？」
仮定： パーティクル は 1つだけで あり 、それ自体をクローン化することはできません。
回答： 粒子P の 量子状態は、N次元ヒルベルト空間のベクトルです。基底ベクトル付き
。 さらに、このベクトルは単一性に正規化されます
、および基底ベクトル
パートIII：猫
量子力学の最も興味深い現象に近づきました。 間違いなく、読者の少なくとも一人は、「量子重ね合わせ」または「量子もつれ」などの用語を聞いています。これらの効果やその他の同様の魔法は、不要な結論を出さない瞬間に始まります。
条件には2つの定義があります。
定義1： 粒子P の 古典的な状態は、セグメントからの数です
仮定： パーティクル は 1つだけで あり 、それ自体をクローン化することはできません。
定義2 ： 粒子Pの量子状態は、 2次元ヒルベルト空間のベクトル ...
通常、結果はいくつかの定義から派生します。ここでは、定義から派生していないものに興味がありますが、それでも調和の結果と呼びます。
系譜1： 量子状態の定義から、粒子がセグメント内のある点にあるということにはなりません 。 一般に、どこからでもすべきではありません。
つまり、パーティクルは一度に2つのポイントに配置できます！ たとえば、量子状態にある粒子の場合
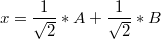ある時点であるということにはなりません。 はい、それは中間のどこか、AとBの間のある地点Mにあるかもしれませんが、これを主張して、不当な自由を示します。
結果2： 量子状態の定義からは、粒子が小さな破片に分割され、いくつかの破片がそこに飛び、他の破片がここにあるということにはなりません 。
これを理解する方法は？ 粒子を一度に2つのポイントに配置し、同時に不可分なままにする方法を教えてください。 シュレーディンガーの猫は生きていると同時に死んでいるという事実に慣れています。つまり、粒子はあちこちに同時に存在するということです。 しかし、彼女は不可分です。 彼女は何を伸ばしましたか？
群れの概念と仮想粒子のインスタンスを紹介します。
パートIV：ロイ
定義No.3： パーティクルインスタンスは、特定の瞬間の空間の位置、時間の経過に伴う動きの軌跡、およびすべての代数的ルールが真である引数とモジュールを含む複素数（振幅と呼ばれる）に対応する仮想オブジェクトです。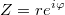
定義4： 群れは標本の集まりです。
定義番号5： 粒子-群れ（空間の量子化の操作を実行する場合）。
複素平面の複素数に対応する矢印が内部にあるボールとしてインスタンスを想像してください。 ボールには1つの移動方向があり、その中の矢印は別の方向、つまり、これらの方向が異なることを理解することが重要です。
しかし、なぜ違うのですか？ 事実、素粒子内部のプロセスは説明が非常に難しいため、これらのプロセスが粒子自体の動きに与える影響を基本的なレベルで予測することはできないため、ボール内部の矢印とボール自体の移動方向との間に関連性はありません。
r 、 φ 、および運動の法則の変化の法則を定義しないと、すべてがそれらに依存するため、ここで完了したばかりの言語操作は役に立ちません。
引数の変動の法則： φは、インスタンスが移動するにつれてdφだけ一定に増加します。
つまり、統合された矢印は常に同じ方向に回転しています。 なぜこれが必要なのですか？ そのため、システムはどのような状況でも進化を停止しません。
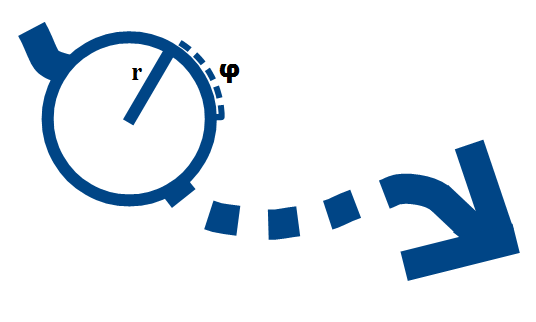
加算と乗算の法則： 単一の軌道に沿って移動すると、振幅が乗算されます。 さまざまな軌道に沿った振幅が加算されます。
この法則は、 「量子力学における重ね合わせの原理」としても知られています。
空間内のインスタンスの運動の法則： 粒子を量子状態で与えます。 空間のあるセルにあるコピーが与えられます（そのセルに対して量子化操作が実行されました）。 この空間のセルの周囲には、隣接するセルがあります。
このプロセスは、インスタンスごとに繰り返されます。
- このインスタンスは、周囲に隣接するポイントが存在するのと同じ回数だけ自身を複製します。
- 各クローンは、それに対応するその隣接ポイントに移動します。
- この父親インスタンスは任意のポイントに移動します
| 1.各ボールの内側には、1つのセルから別のセルへのインスタンスの移動ごとに角度dφで回転する同じ複雑な矢印があります。 | 2.したがって、絶えずクローンを作成する巨大な動的システムがあります。
| 3.一般に、最初の標本の移動方向が群れの動きを決定しますが、それでも群れはすべての方向に広がります。 単一のインスタンスの動きを（クローンに注意を払わずに）トレースすると、絶対にランダムな軌道に沿って動きます。 |
各ボールの内部には、独自の方向と長さを持つ複雑な矢印があることを忘れないでください。 特定の瞬間に、空間内の任意のセルに表示される矢印を予測する方法は？ 明らかに、このためには、前の瞬間にシステム全体に何が起こったかを知る必要があります。 微分方程式が得られます（それを発見したシュレディンガーを称えてシュレディンガー方程式と呼ばれます）。
空間内のインスタンスの運動の法則： Let-粒子の量子状態、空間のすべてのセルの振幅が次々に書き込まれる列ベクトル。
-インスタンス間の相互作用の方法を決定するエネルギー演算子。 その後、群れは次の法則に従って移動します。
。
「ハンドル付きのピース」のエネルギー演算子の形成については、次の記事で検討します。
構造的に、次の概念を見つけました。
- 数としての粒子の古典的な状態 （他とは異なります）
- ベクトルとしての粒子の量子状態 （「一度に複数の場所にあるもの」としてではない）
- 群れとしての粒子 （量子化操作を実行する場合）
- Swarm Superpositionの原理。これにより、振幅は1つの軌跡に沿って乗算され、あらゆる種類の軌跡に沿って追加されます。
- 標本の移動の法則
次の記事では、最も興味深い-任意の数のパーティクルを含むシステムについて検討します。 テンソルとは何か、絡み合った状態を分析し、最後に、量子進化を「模倣」し、それを便利に描画できるプログラムを作成します。
量子力学のトピックは最近活発に普及しているので（関連する雑誌から始まり、「量子もつれ」に専念する展示全体で終わります）、現在の状態を監視して「私たちと一緒にいるもの」をチェックする必要があるように思えます「おそらくこの情報は役に立つでしょう-pleaded.ru