エピグラフの種類
特許では、人/チームが発明したものではなく(例えば、接着剤など)、特許されたときに発明のカテゴリーがあり、緊急の目標を達成するための新しい方法ではありません(例えば、傷を感染から密封する)。 そして、例えば、特許取得済みは、完全に新しい(特定の物質について)だけでなく、目的の用途を達成するためによく知られ、長く知られている物質の使用です。 「そして、BF-6接着剤で傷を封じてみようか? ああ! そして、それは殺菌特性を持っていることがわかります...そして、傷の下の呼吸は...そしてより速く治癒します! 出資して応募してください!」
応用数学には、非常に広範囲のさまざまな問題を解決できる有能なツールがあります。 これについてお話ししたいと思います。 誰かが、成功裏にマスターされたアルゴリズムまたはテクニック/プログラムの非自明なアプリケーションの検索に出くわすかもしれません。 厳密な数学的ツールや関係への言及はほとんどありません。数値法の利点と応用のより定性的な分析は、私の人生で大きな役割を果たし、重要な職業上の問題を解決するための基礎になりました。
かなり前(論文を擁護し、クラスノダールの軍事宇宙企業で働いていたとき)最適化問題を解決するためのツールキットが開発されました-そのパラメーターの特定の制限セットでマルチパラメーター関数の極値を検索します。 このような方法は広く知られています。たとえば、ほとんどの人が最急降下法( Gradient Descent )に精通しています。
ソフトウェアパッケージ(最初はFortran、次にPascal / Modula 2、今ではアルゴリズムは十分に継承され、便利で汎用的なVBA / Excelにあります)は、非常に幅広いクラスの問題で互いに補完する極値を見つけるためのいくつかの異なる既知の方法を実装しました。 それらは簡単に交換でき、スタックにインストールされました(次のスタックは、前のスタックで見つかった最適なものから始まり、パラメーターの可能な初期値を幅広くカバーしています)、すぐに最小値を見つけ、目的の関数を「絞り込み」、見つかった極値のグローバル性を保証します。
たとえば、この一連のプログラムを使用して、ソーラーパネル、バッテリー(長持ちするニッケル水素のみが出現)、ペイロードおよび制御システム(バッテリーの向きと負荷のエネルギー変換)で構成される自律システムのモデルが作成されました。 これはすべて、特定の地域の外部気象条件の影響下で、特定の期間に推進されました。 このために、「 統計的ブートストラップ 」法を使用して、気象モデルも作成されました(
プロセスの出力でのフォトセルのシリコンウェーハの測定と、最適化方法による単一要素のモデルのパラメーターの識別により、太陽電池の生産のための現在の製造プロセスの統計パラメーターを記述する要素パラメーターの配列を作成することが可能になりました。
太陽電池の電流-電圧特性(CVC)の数学モデルはよく知られており、そこにはほとんどパラメーターがありません。 最小標準偏差を持つ太陽電池のI-V特性のパラメーターを選択することは、目的関数の最小値(I-V特性の偏差の平方)を見つける古典的なタスクです。
モンテカルロ法によって得られた完成した太陽電池のパラメーターは、要素の接続の特定の構造に対するパラメーターの確率的広がりを反映していました。 太陽電池モデルから組み立てられたバッテリーモデルの構築により、特に、損傷(アフガニスタンでの戦争が本格化し、met石が宇宙を飛んでいた)と部分的な陰影(雪、紅葉)による損失によるバッテリー電力損失の推定の問題を解決することができました)、これにより危険なブレークダウン電圧が発生し、平均電力損失を減らすためにシャントダイオードを正しく配置する必要が生じました。 これらはすべて、すでに確率的なタスクでした。 「ブリック」の初期パラメータ、バッテリー接続スキーム、および影響要因のさまざまなばらつきを伴う膨大な計算が必要です。 そのような計算で太陽電池の主要な特定モデルから「踊る」ことは不利であったため、一連のモデルが構築されました:主要なシリコンウェーハ、それが組み立てられたバッテリー全体(ブロック図の分析が必要な場合)、およびバッテリー自体。 これらのモデルのパラメーターは、最適化手法を使用して特定され、その計算のためのバッテリー構造の要素の配列は、確率的変動を考慮したモンテカルロ法によって生成されました(パラメーターの配列+統計ブートストラップ)。
解決されるタスクはより複雑になりました。 当初、アセンブラで最適化手法の最も「計算集約的な」部分を作成するというアイデアがありましたが、生産性が向上するにつれて、最初はSMコンピューター(タスクは一晩で考慮されました)、次にPC(今では最も複雑なタスクには1時間か2時間かかります)最適化(トートロジーの傑作)はなくなりました。 さらに、ほとんどの場合、目的関数自体は「計算集約的」です。
ここで、部分的に影響を受ける最適化手法の普遍性に戻り、それらを数値解析の他の手法に関連付ける必要があります。 開発したツールの主な用途:
-初期(実験または計算)データによる理論モデルのパラメーターの識別。
-データ近似。これは、モデルだけでなく、平滑化/近似、補間、および外挿を目的とした適切な(一般的に抽象的な)数式のパラメーターの同じ識別です。
-任意の(!)方程式のシステムの数値解。
少しのように見えますが、このクラスの問題は、産業、科学における数学の実際に応用された幅広い問題を「カバー」します。自律システムのモデルの例は、この証拠です。
数値解析の古典的な方法の兵器庫には、いくつかの標準的な問題を解くための効果的な直接的な方法/アプローチ(たとえば、低次の多項式を含む連立方程式)があり、特別なプログラムライブラリが開発されています。 ただし、パラメータ/未知数の数が4-5を超える(および計算コストが劇的に増加する)場合、および/または方程式の形式が古典(多項式などではない)から遠い場合、そして原則としてすべてがより複雑です(初期データノイズの多いエラーや測定エラー)、既製のライブラリプログラムは無効です。
人生から最適化問題を解決するために開発されたツールを比較的最近使用したことから、もう1つの例をさらに詳しく説明します。
実験(フィールド)データに関するいくつかの論文では、これらのデータを説明する理論モデルの識別が必要であり、隣接する技術プロセスの効率を改善するための実際の推奨を行うことができました。 プロセステクノロジーの改善の各割合は、世界中のファーストクラスによるフィールドトライアル(および近くのビーチ)への繰り返しの旅と、フィールドを走るだけのシックなレクサスジープの取得を正当化しました(そして、ボルシチを調理する方法を知っている素敵な長い脚のブロンドでも:) 問題は、そのようなモデルがいくつかあり、実験データの再現の識別と品質がそれらのいずれかの適用性を選択できることであり、これらのモデルのパラメーターは6から9であり、サンドイッチの法則に従って潜在的に最も有用なモデルは最も複雑でした。
以下は、初期の実験データ(X、Y、Z)、19の測定値です。
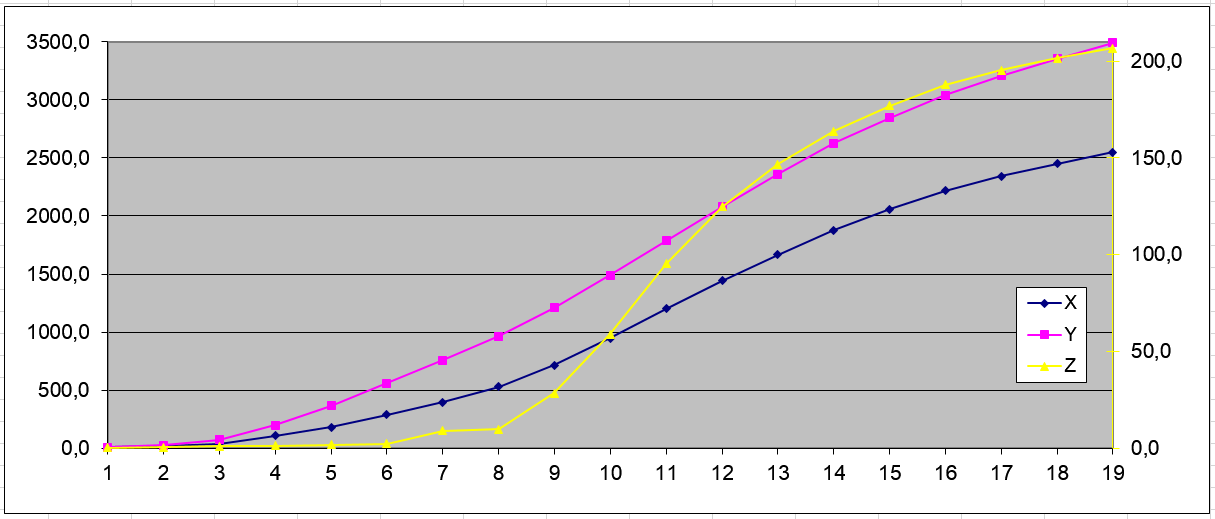
また、最も複雑な9パラメーターモデル(a1 ... a9-モデルパラメーター)を識別する場合の曲線近似の例(U3-実験、U3R-モデルによる計算):

このモデルの式は次のとおりです。
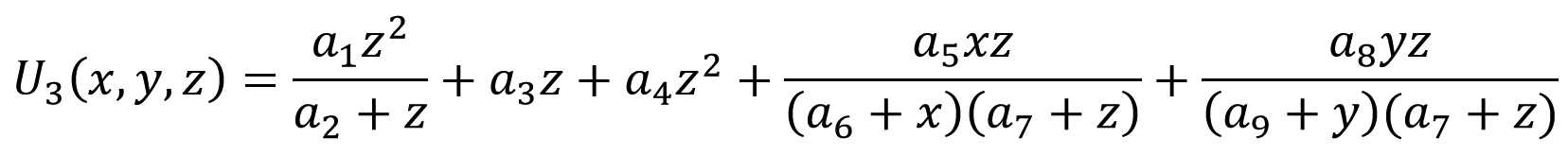
このような作業が必要な場合-提供されたデータに基づいて計算を行い、結果を電子メールで送信して、開発されたマットの利点を評価できます。 装置。
これは、科学、生産、学位論文の作成、深刻な卒業証書、データ処理、モデル構築における一般的なタスクの範囲です。 さらに、提供された結果によると、誰もが実際に達成された計算精度を評価できるため、不正は除外されます。
データ処理の問題を説明してください-そして、解決策を見つける方法を見つけるでしょう、プログラムは動作するはずです!
おそらく、新しい応用分野で説明されていることを外から見てみたいです。 有益なコメントと協力に感謝します。