PARI / GP：有限フィールド計算。 パート1

PARI / GPを選ぶ理由

PARI / GPは、計算数論に焦点を当てた、独自のCライクな解釈言語を備えたコンピューター数学システムです。 このシステムは科学界で人気があります。2014年のGoogle Scholarによると、PARI / GPを使用した約100の特集記事が、査読付きの雑誌/会議で公開されました。



私の論文の研究では、線形代数の従来の問題を解決する必要がありました（たとえば、大きな次元の行列の場合、そのカーネルとランクを計算します）が、有限体（たとえ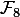ば、 または 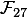） 複雑な行列だけがあれば、少なくともいくつかの有名な記号数学システムはすべて効果的に対処できます。たとえば、私のお気に入りのWolfram Mathematicaでは 、それぞれNullSpace関数とMatrixRank関数を使用するだけで十分です。 一般的な線形代数アルゴリズムの非効率性のためにパフォーマンスが低下するものの、同じ関数が有限体上の行列で一度に機能するのは素晴らしいことです...悲しいかな、私は指数関数的な成長を受け取りました）行列の次元の計算時間（Wolfram Mathematicaプロファイルフォーラムの私の質問を参照） 確かに、公平に言えば、これは線形代数アルゴリズムの実装の問題によるものではなく、シンボリック計算プロセッサ自体の問題によるものではありません。



私の大きな喜びは、PARI / GPは、さまざまな代数システム（リング、フィールド）での計算に特化しており、組み込み型のシンボリック構造としてではなく、「原子」数として要素を操作することです。 私の経験的な観察では、PARI / GPはそのような計算の卓越した速度を持っています。 さらに、解釈されたコードを純粋なCに変換することもできます。

最終フィールドで作業するための主な機能

以下の説明は、非常に「高レベル」であり、PARI / GP内で使用されるアルゴリズムとデータ構造に言及していません（今後の投稿のトピック）。

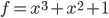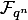• 関数ffinit（q、n、{v}）は、 単純体で正規化された既約を計算します 変数vからの次数nの多項式f（v）（オプションのパラメーター。デフォルトでは、多項式は引数xから得られます）。 例：ffinit（2、3、x）を呼び出すと、原始多項式が返されます 、およびffinit（2、4、x）はすでに既約多項式です 。 これで拡張子を設定できます 最終フィールド 古典的に因子環のような 。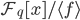
• 根 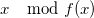PARI / GPオブジェクトとしての既約多項式f（x）は、ffgen（f、x）関数を使用して作成されます。 言い換えると、呼び出しg = ffgen（f、x）は、等価クラス[x]で識別されるオブジェクトgを返します-因子環の要素 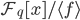。 今フィールド 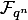上の線形空間とみなされる 、生成セットを使用して（その加算テーブルと乗算テーブル）を構築できます 。
• ffprimroot（g）関数を使用して、プリミティブフィールド要素を見つけることができます。 この関数は、gで与えられる有限体の乗法群の次数（n-1）のランダムな要素を計算します。
• minpoly（a）関数を使用すると、有限体の要素aの最小多項式を見つけることができます。 たとえば、p = minpoly（a）を呼び出すと、 。 言い換えれば、原始的なフィールド要素を見つける 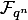、フィールドは従来の形式で表すことができます ここで、pはその原始多項式です。

人生の例

予備ヘルプ

既に述べたように、PARI / GPは独自のCのような言語を使用します。 詳細なガイドはこちらにあります 。 以下は、以下の例（およびそれ以上）のいくつかのポイントを説明する簡単な説明です。

1. PARI / GPのすべてのオブジェクトは、内部スタックに作成されます。 デフォルトでは、内部スタックは3.8MB（400万バイト）のコンピューターの動的メモリーを占有します。 拡張するには、関数allocatemem（s）が使用されます。ここで、sは要求されたバイト数です。
2. 区切り文字「;」 行の最後は結果の印刷を禁止するために使用されます。
3. デフォルトでは、識別子は多項式の変数です。 識別子の前にアポストロフィを使用できます。これは、これが多項式の変数であり、オブジェクトではないことを示します。 例えば
   
   

   x = 12; type(x) >"t_INT" type('x) >"t_POL"
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
4. 中括弧 "{"、 "}"は、コマンドのグループ化（たとえば、複数行）にのみ使用されます。 グループ化は、内部で宣言されたオブジェクトのスコープ（寿命）を指定しません。 デフォルトでは、宣言された変数はすべてグローバルです。 オブジェクトがローカルに接続されるようにするには、my修飾子を使用して宣言する必要があります。 例えば
   
   

    { x = 12; } x >12 { my(y = -13.2); } y >y
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
5. PARI / GPを使用すると、ユーザーはラムダ関数を作成できます。 構文は次のとおりです。lambda=（argument list）-> function body;

例自体

 createField = (q, n, var) -> ffgen(minpoly(ffprimroot(ffgen(ffinit(q, n, var), var))), var); a = createField(2, 4, 'x) >x fforder(a) \\     >15 allocatemem(2^27); \\  128     PARI/GP M = matrix(1000, 1000, i,j, random(a)); \\   10001000    GF(16) {gettime(); matrank(M); gettime()} \\   ()      >34209 {gettime(); kernel(M~); gettime()} \\         >88425
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私のラップトップ構成はIntel Core（TM）i7-4702M CPU @ 2.20GHz 2.20GHz、32kB L1キャッシュ、8Gb DDR3です。 私はPARI / GP 2.7.2（32ビット、シングルスレッド）を使用しました。これは、このテキストの公開時点での最新リリースであり、Windowsで「箱から出してすぐに」です。