コース内容
- 記事1:Bresenhamのアルゴリズム
- 記事2:三角形のラスタライズ+背面のトリミング
- 記事3:非表示のサーフェスの削除:z-buffer
- 記事4:必要なジオメトリ:マトリックスフェスティバル
- 4a:透視歪みの構築
- 4b:カメラを動かし、これから何が続くか
- 4c:新しいラスタライザーと透視歪み補正
- 記事5:ライブラリにシェーダーを作成する
- 記事6:単なるシェーダー以上:影のレンダリング
コード改善
公式の翻訳(少し磨き上げたもの)はこちらから入手できます。
建物の遠近歪み
4番目の記事は2つに分けられます。最初の部分では遠近法の歪みの構築について、2番目の部分ではカメラの移動方法とその後について説明します。 今日のタスクは、これらの画像を生成する方法を学ぶことです。

平面ジオメトリ
平面の線形変換
平面上の線形表示は、対応するマトリックスによって定義されます。 ポイント(x、y)を取得すると、その変換は次のように記述されます。

最も単純な(非縮退)変換は恒等行列によって与えられ、すべてのポイントをそのまま残します
マトリックスの対角線上の係数は、平面の伸縮を指定します。 図で説明しましょう。たとえば、次の変換を記述した場合:
その白いオブジェクト(カットオフ角度のある正方形)は黄色に変換されます。 赤と緑のセグメントは、それぞれx軸とy軸に沿った単位ベクトルを与えます。
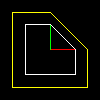
この記事のすべての写真は、 このコードによって生成されます。
なぜマトリックスを使用するのですか? 便利だから。 まず、マトリックス形式で、オブジェクト全体の変換を次のように記述できます。
ここで、変換は前の例と同じですが、2行5列のマトリックスは、切り取られた角度を持つキューブの座標の配列にすぎません。 配列全体を取得し、変換を掛けて、変換済みのオブジェクトを取得しました。 きれいですか? さて、私は同意します。
本当の理由は、非常に定期的に、オブジェクトが連続していくつかの変換を受けることです。 コードに型変換関数を書くと想像してください
vec2 foo(vec2 p)return vec2(ax + by、cx + dy);
vec2 bar(vec2 p)return vec2(ex + fy、gx + hy);
[..]
for(オブジェクトの各p){
p = foo(bar(p));
}
このコードは、オブジェクトの各頂点で2つの線形変換を行い、それらは数百万単位で計算されます。 そして、多くの場合、1ダースの変換が必要です。 高価な マトリックスアプローチでは、すべての変換マトリックスを乗算し、オブジェクトを1回乗算します。 乗算では、括弧を必要な場所に配置できますか?
会話を続け、対角要素が軸方向のスケーリングを提供することを知っています。 他の2つの行列係数は何に責任がありますか? 次のような変換を見てみましょう。
一致する画像:
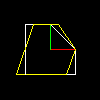
x軸に沿った単純なシフトにすぎません。 2番目の反対角要素は、y軸に沿ってシフトします。 したがって、平面上の基本的な線形変換は、軸方向の伸縮と軸方向の変位の2つだけです。 待って、彼らは私に言うが、例えば、原点の周りの回転はどうだろうか?
回転は3つのシフトの合成として表現できることがわかります。ここでは、白いオブジェクトが最初に赤、次に緑、次に青に変換されます。
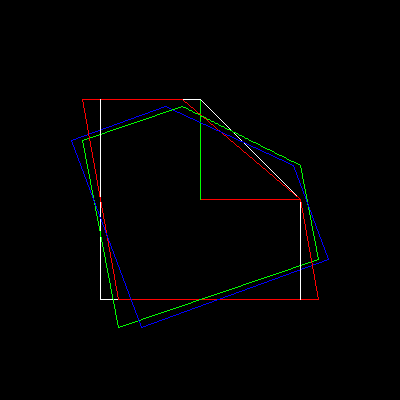
しかし、極端に行かないように、原点の周りの反時計回りの回転行列は直接書くことができます(括弧の配置を覚えていますか?):
もちろん、任意の順序で乗算できますが、行列の場合、乗算は可換ではないことを忘れないでください。
通常、シフトしてから回転(赤いオブジェクト)するのは、最初に回転してからシフト(緑のオブジェクト)するのと同じではありません。

平面上のアフィン変換
つまり、平面上の線形変換は、ストレッチとシフトの合成です。 つまり、変換のマトリックスが何であっても、原点は常に原点に移動します。 したがって、線形変換は素晴らしいですが、基本的な並列転送を想像できない場合、私たちの人生は悲しくなります。 それともできますか? しかし、それを個別に追加し、アフィン変換を線形部分と並列転送の構成として記述するとどうなりますか? このようなもの:
これはもちろん素晴らしい記録ですが、そのような2つの変換の構成がどのように見えるかを見てみましょう(実生活では何十もの変換を蓄積できる必要があることを思い出します)。
単一のコンポジションでは、すでに非常に不快に見え始めます。 この式を変換して、線形部分+平行移動という形式の1つの変換のみをオブジェクトに適用してください。 個人的に、私は本当にこれをしたくありません。
同次座標
どうする? 召喚! 変換行列に1行と1列を手で追加し、変換するベクトルのユニティに等しい3番目の座標を追加するとします。
この3x3行列とベクトルに1を加えて乗算すると、3番目のコンポーネントに単位を持つベクトルが再び得られ、他の2つはまさに望みの形になります! 魔術。
実際、この考え方は非常に単純です。平行移動は、2次元空間での線形操作ではありません。
したがって、2次元空間を3次元に浸します(3番目のコンポーネントにユニットを追加します)。 これは、2次元空間が3次元内部の平面z = 1であることを意味します。 次に、3次元空間で線形変換を行い、3次元空間全体を物理面に投影します。 これからの並列転送は線形になりませんでしたが、パイプラインはまだ単純です。
3次元空間を平面にどのように投影しますか? 非常にシンプル:
ほんの少しですが、ゼロで割ることはできません!
誰が言ったの? 冗談。 何が再び起こっているのかを理解しましょう。
- 2次元空間を3次元に浸し、平面をz = 1にします
- 3Dでやりたいことをする
- 2Dに投影する各ポイントについて、原点とこのポイントの間に線を引き、物理面z = 1との交点を探します。
この図では、物理面は紫色であり、点(x、y、z)は点(x / z、y / z)に投影されます。
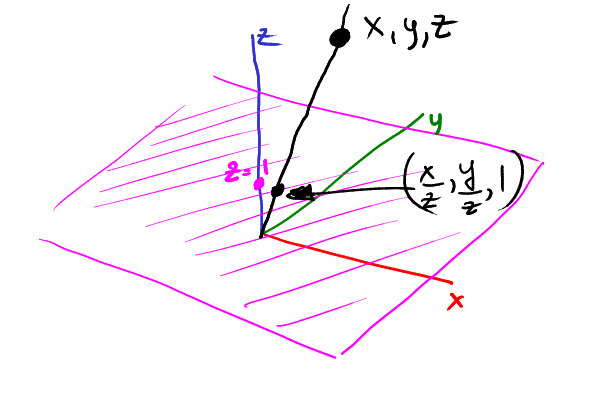
ここで、ポイント(x、y、1)を通る垂直レールを想像してみましょう。 ポイント(x、y、1)はどこに投影されますか? もちろん、(x、y):
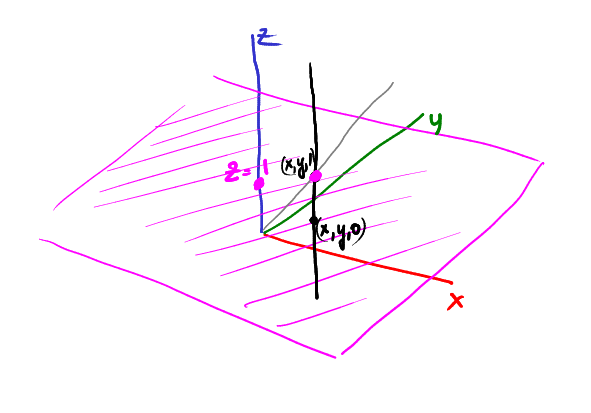
ここで、レールを下にスライドさせてみましょう。たとえば、ポイント(x、y、1/2)は(2x、2y)に投影されます。

スライドを続けます:ポイント(x、y、1/4)は(4x、4y)に投影されます:
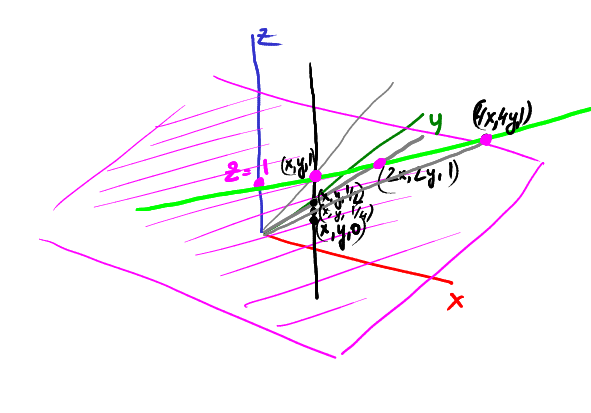
zに沿ってゼロまでスライドし続けると、投影は方向(x、y)の座標の中心からますます遠くなります。
つまり、点(x、y、0)は、方向(x、y)の無限遠点に投影されます。 これは何? そうです、これはベクトルです!
同種の座標により、ベクトルと点を区別することができます。 プログラマーがvec2 v(x、y)を記述した場合、それはベクトルですかドットですか?
言うのは難しいです。 そして、同次座標では、3番目のコンポーネントにゼロがあるものはすべてベクトルであり、他のすべてはエンドポイントです。
参照:vector + vector = vector。 ベクトル-ベクトル=ベクトル。 ポイント+ベクトル=ポイント。 素晴らしいですね
複合変換の例
私はすでに、何十もの変換を蓄積できる必要があると言ってきました。 なんで? 点(x0、y0)を中心にフラットオブジェクトを回転させる必要があるとします。 どうやってやるの? 私たちはすべてのツールを持っているので、あなたは行って式を探すか、自分でそれを行うことができます。
座標の中心を中心に回転でき、シフトできます。 他に何が必要ですか? x0、y0を座標の中心に移動し、回転させて戻ります。 景品!
3Dでは、アクションのシーケンスはもう少し長くなりますが、意味は同じままです。いくつかの基本的な変換を行うことができ、それらの助けを借りて、あらゆる種類の複雑な変換をエンコードできます。
待って、3x3マトリックスの一番下の行に触れる権利がありますか?
なんてこった! この変換を適用しましょう:
標準のテストオブジェクトに。 テストオブジェクトは白、ユニットXとベクターのプレーヤーはそれぞれ赤と緑で表示されることを思い出してください
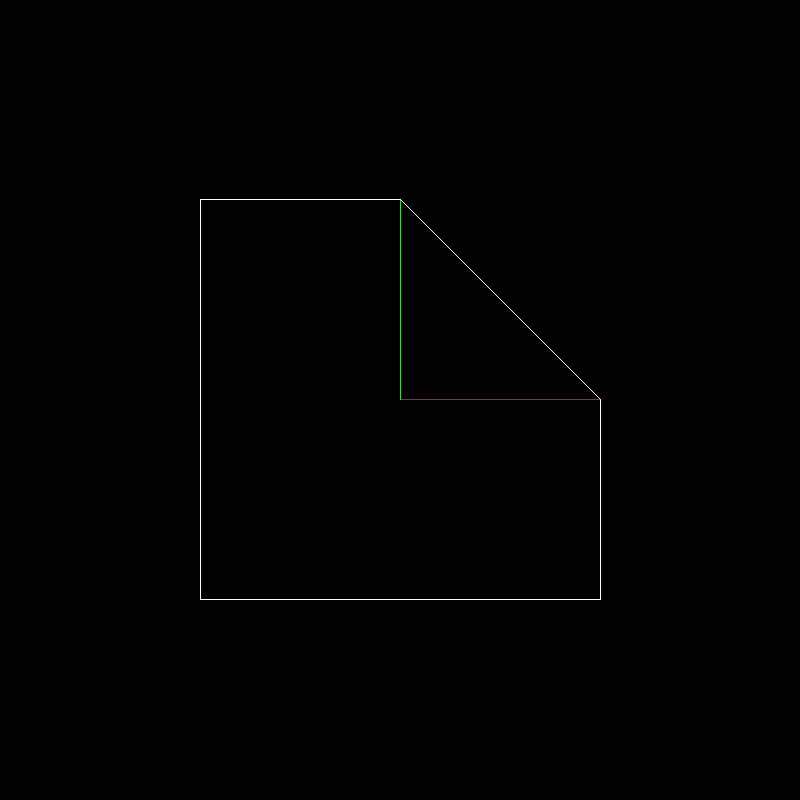
変換されたオブジェクトは次のとおりです。

そして、ここから楽しみが始まります。 プレイバッファエクササイズを覚えていますか? ここでは、ほぼ同じことを行います。
2次元のオブジェクトをラインx = 0に投影します。 次に、タスクを複雑にします。投影は中心になり、カメラはポイント(5、0)にあり、原点を確認します。 投影を見つけるには、カメラポイントとオブジェクトの各頂点を通る線(黄色の線)を描画し、直接スクリーンとの交点(白い垂直線)を見つける必要があります。
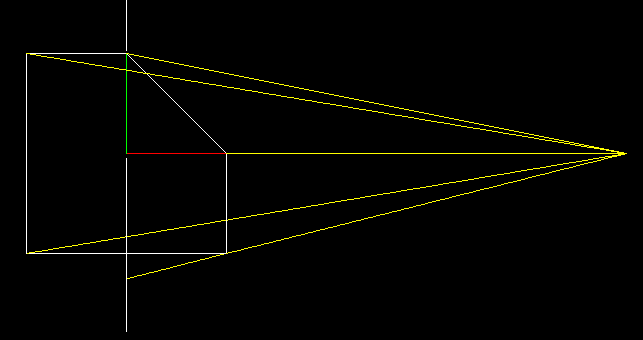
そして、元のオブジェクトを削除して、代わりに変換されたオブジェクトを描画しましょう。
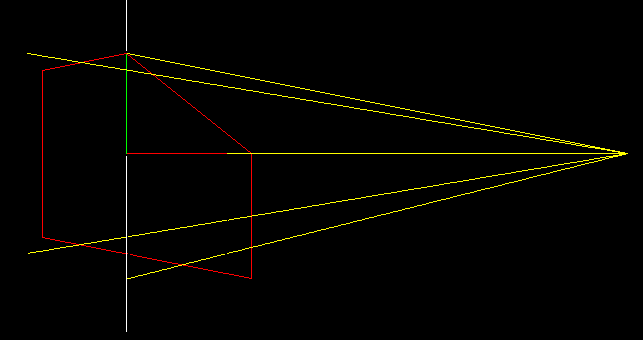
変換されたオブジェクトの通常の正射影を使用すると、まったく同じポイントが見つかります!
結局のところ、このマッピングは何をするのでしょうか? 各垂直エッジを垂直のままにしますが、同時にカメラに近いものを伸ばし、カメラから遠いものを圧縮します。 張力と圧縮の係数を正しく選択すると、単純な正射影で透視歪みの画像が得られるという効果が得られます! 次の段落では、1つのディメンションを追加し、-1 / 5ファクターがどこから来たかを示します。
次の3つの次元に移りましょう
今起こった魔法を説明しましょう。
2次元アフィン変換の場合と同様に、3次元空間でも同次座標を使用します。
ポイント(x、y、z)を取得し、4次元空間に浸し、4番目のコンポーネントに1を追加し、4次元に変換して、3 dに投影し直します。 たとえば、次の変換を行います。
3Dへの投影により、次の座標が得られます。
この結果はよく覚えていますが、数分延期します。 均一な座標や他のエキゾチックなものなしで、通常の3Dの中心投影の標準定義に戻りましょう。 点P =(x、y、z)があり、これを平面z = 0に投影したい場合、カメラは座標の中心から距離cのz軸上にあります。

三角形ABCとODCが似ていることを知っています。 つまり、次のように記述できます| AB | / | AC | = | OD | / | OC | => x /(cz)= x '/ c。
三角形CPBとCP'Dを考慮すると、y座標について同様の記録に簡単に到達できます。
したがって、これは均一な座標を介した投影の結果に非常によく似ており、1つの行列の乗算であるとみなされた場合のみです。 係数r = -1 / cの依存性を導き出しました。
材料を統合するには:今日の主な処方
前のテキスト全体を理解せずにこの式をとっただけなら、私はあなたが嫌いです。 したがって、 原点から距離cの z軸にある(重要!)カメラを使用して中央の遠近法を構築する場合、最初に3次元の点を4次元空間に浸し、1を追加します。次に、次の行列を乗算して結果を3Dに戻します:
オブジェクトを変形して、今度はプロスペクトでワイヤーレンダリングを作成するために、新しく取得した座標zを忘れるだけです。 Zバッファーを構築する場合は、もちろん、それを使用します。 コードのスナップショットはgithubで入手できます。 彼の仕事の結果は、私たちの記事の冒頭で見ることができます。