
プログラムの概念から始めましょう。 数学的な観点から見ると、プログラムは関数です。 時々これは明らかではないかもしれません。 プログラムが関数の場合、引数が何であり、何が返されるかを決定する必要があります。 bcのような単純なユーティリティの場合、すべてが明確です。引数はstdinの式であり、結果はstdoutの結果です。 より複雑なケースでは、プログラムが関数であるという結論に達することもできます。 たとえば、DBMSを考えてみましょう。この場合、プログラムは関数でもあり、引数を使用してuser-spaceに割り当てられたメモリを取得し、継続的に実行しながらそれを返します。 それはかなり次善の例かもしれませんが、理解できます。
プログラムが関数である場合、この関数を取得する手段がどのようなものになるかを検討する必要があります。 それはすべてプログラミング言語に依存し、それらはそのようなツールです。 そして、それが関数型言語、手続き型、命令型、宣言型などであるかどうかにかかわらず、それらはすべて明示的または暗黙的な構成を使用する傾向があります。 構成の概念を定義する時が来ました。 2つの関数を与えましょう
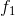 そして
そして  、それらから関数を作成できます
、それらから関数を作成できます  それらに機能を適用する
それらに機能を適用する 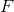 :
: ) 。 他の関数を引数として取るこのような関数Fは、 compositionと呼ばれます。 そして、構築方法
。 他の関数を引数として取るこのような関数Fは、 compositionと呼ばれます。 そして、構築方法  多くの場合がありますが、それぞれの方法は合成です。 分岐構成と重ね合わせ構成のサンプル構成をいくつか検討してください。
多くの場合がありますが、それぞれの方法は合成です。 分岐構成と重ね合わせ構成のサンプル構成をいくつか検討してください。
支店組成物。 2つの関数を与えましょう
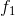 そして
そして  同様に1つの述語
同様に1つの述語  (同じ関数ですが、定義されているセットの要素ではなく、値「true」または「false」を返します)。 そのような機能があります
(同じ関数ですが、定義されているセットの要素ではなく、値「true」または「false」を返します)。 そのような機能があります  どれ
どれ 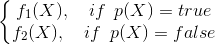 。 この場合、彼らは、関数
。 この場合、彼らは、関数  分岐操作によって取得されたため、この操作を
分岐操作によって取得されたため、この操作を  それから
それから ) 。 コンポジションを関数に適用すると、新しい関数を取得して使用できます。
。 コンポジションを関数に適用すると、新しい関数を取得して使用できます。
重ね合わせ構成 。 設定しましょう
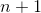 機能
機能  どこで
どこで 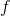 -
- 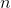 -ary関数とそのような関数があります
-ary関数とそのような関数があります 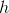 次のように定義されます
次のように定義されます ,f_2(X),...f_n(X))) 。 この場合
。 この場合 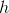 重ね合わせ演算を使用して取得されたとみなされます
重ね合わせ演算を使用して取得されたとみなされます 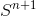 :
: ) 。
。
これらの操作のプロトタイプをプログラミング言語で検討してください。 どこかでより明確で、どこかより少ない。 C言語では、分岐操作は明らかに制御構造に隠されています
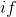 :
: if(p(X)) f1(X); else f2(X);
最初のケースでは、表現ではなくステートメントが考慮されましたが、これはプレゼンテーションに干渉しませんp(X) ? f1(X) : f2(X);
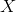 たとえば、スコープ内の変数のセット全体など。 LISPでは、この構成のプロトタイプは次のようになります。
たとえば、スコープ内の変数のセット全体など。 LISPでは、この構成のプロトタイプは次のようになります。 (if (p X) (f1 X) (f2 X))
Haskellでは、次のようになります if p X then f1 X else f2 X
どちらか
gx | px == True = f1 x | px == False = f2 x
重ね合わせの操作について話すと、多くのプログラミング言語ではさらに目立たなくなりますが、それでも遍在しています。 C言語の重ね合わせ演算により、次の置換が可能になります f(f1(X), f2(X), f3(X));
LISPでは、次のようになります (f (f1 X) (f2 X) (f3 X))
Haskellと同じ f (f1 x) (f2 x) (f3 x)
提案されたすべての機能のアリティが統一されるべきであることにすぐに注意する必要があります。そうしないと、それらへの合成メカニズムの適用が著しく困難になる可能性があります。 Xは実際には次のようなものです
 。
。
明らかに、コンポジションはプログラミング言語の構文に深く「埋もれて」おり、暗黙的にそれらに含まれています。 しかし、洗練された読者なら当然気付くことができるように、新しいものは何もありません。 Edsgar Dijkstraでさえ、彼の著書「プログラミングの規律」でこれに気付きました。
曲を使う
上記に関連して、多くの疑問が生じます。 特に、構成が明示的に使用されないのはなぜですか? 実際、組成物の使用は明確に多くの利点をもたらす可能性があります。 特に、プログラミングプロセス自体を考慮することが可能になるため、複雑なプロジェクトの開発を最適化できます。 結局のところ、プログラマーは現在どのようにプログラミングしていますか? 彼は絵を描くアーティストとしてこれを行います。 言い換えれば、デザインの決定は、彼の経験、予感、同僚のアドバイス、いくつかの個人的な美的信念に基づいて行われます。 しかし、この考え方は、プログラムでファイルに単純に入れることはできません。 つまり プログラムはありますが、それを導いた一連の思考はありません。 これが最初の質問です。 なぜ言語はそのような構文を持っているのか、なぜ言語の作成者はまさにそのような制御構造のセットを定めているのか? なぜ彼らのセットは独断的なのですか? 他の制御構造を追加する必要がある場合の対処方法。
これらの質問は、組成物の適用と生成の手段を解決するのに役立ちます。 人による任意の複雑なタスクの解決策は、分析/分解、そして合成に縮小されるため、このプロセスは構成メカニズムによって有機的にサポートされます。 結局、コンポジションは、タスクが分割されたパーツを接着する正確な接続要素になります。 まあ、人は何らかの方法でタスクを壊さなければなりません、それはまさに彼の特権であり、タスクの構文設計ではありません。 残念ながら、これまでのところ、作曲の概念に合わせて調整された単一の言語は認識されていません。
理解を深めるために、コンポジションを使用して最大公約数(GCD)を見つける例を検討してください。 電卓は、除算の残りを見つけることができます(
 )、整数除算を実行します(
)、整数除算を実行します( 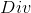 )、不等式述部を計算します(
)、不等式述部を計算します( 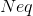 )、ゼロを生成(
)、ゼロを生成(  ) すべての関数は、ゼロのない自然数のセットで定義されます。 したがって、提案されている代数には次の関数があります。
) すべての関数は、ゼロのない自然数のセットで定義されます。 したがって、提案されている代数には次の関数があります。  = {
= { 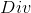 、
、  、
、  、
、 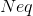 、
、 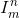 }。 読者は別の機能に気付くかもしれません-
}。 読者は別の機能に気付くかもしれません- 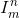 、いわゆるセレクター関数。
、いわゆるセレクター関数。 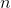 引数は変更されずに戻ります
引数は変更されずに戻ります 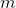 番目、それは必要です。
番目、それは必要です。 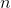 -ar関数。 さらに、サイクリング構成が利用可能です、それを呼び出しましょう
-ar関数。 さらに、サイクリング構成が利用可能です、それを呼び出しましょう 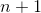
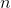 -ary関数
-ary関数  同様に
同様に 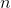 -ar述語
-ar述語  。 反復的に、各関数は次の反復の引数の1つを評価するため、
。 反復的に、各関数は次の反復の引数の1つを評価するため、 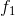 計算する
計算する 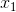 、
、  計算する
計算する  など 反復プロセスは、述部の値がtrueになるまで続きます。 ループ操作への引数は、次の順序で渡されます。
など 反復プロセスは、述部の値がtrueになるまで続きます。 ループ操作への引数は、次の順序で渡されます。 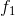 最後の反復で取得
最後の反復で取得 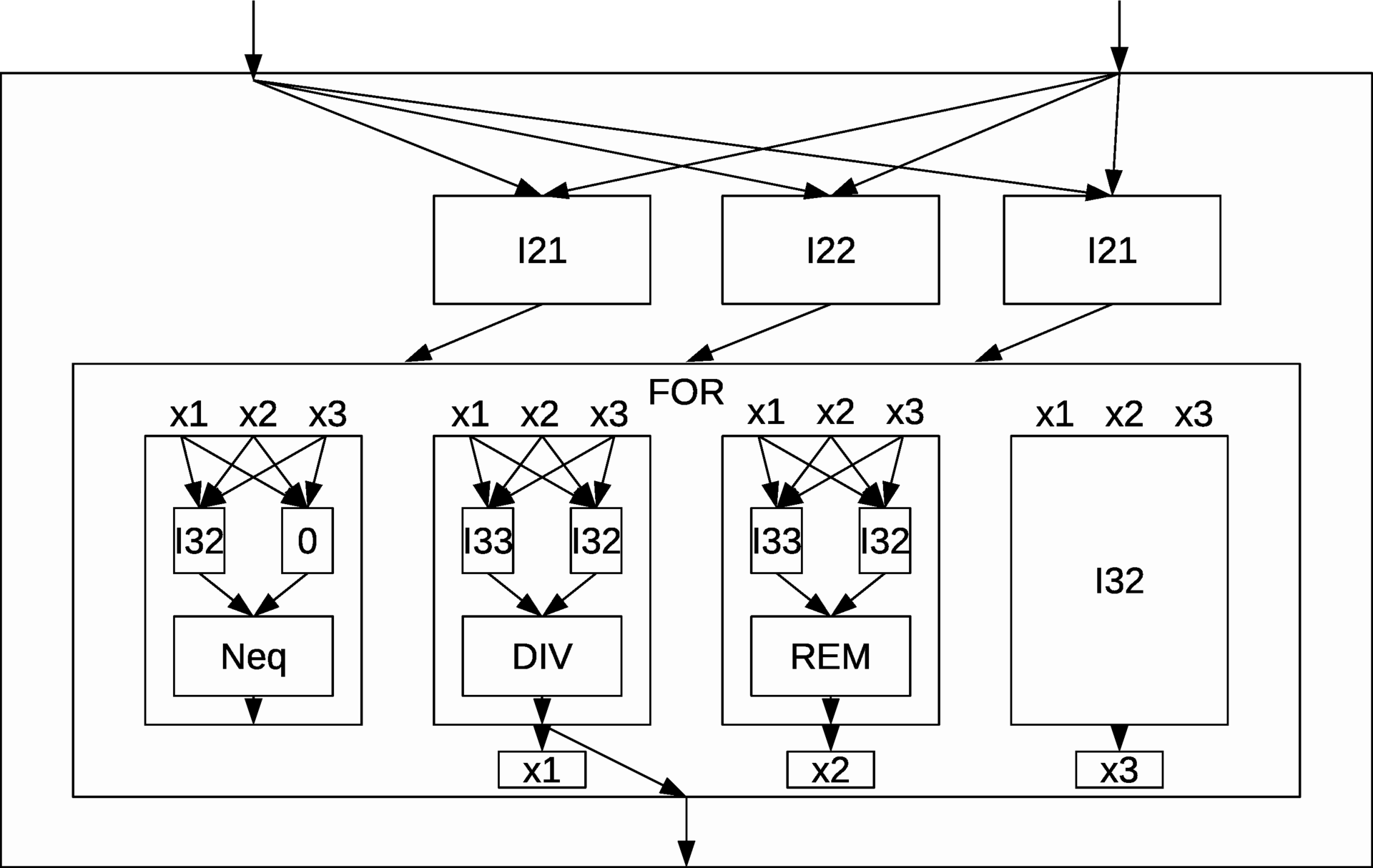
したがって、アルゴリズム自体を「数学の言語」で定式化することが可能になります。つまり、数学的な手段で研究できるため、人が書くプログラミング言語ではなく、実際には、さまざまな言語の根底にある構成を反映します。
ソリューション自体への組成的アプローチは、A.I。 Maltsev(Maltsev代数)、学者Glushkov(アルゴリズム代数)。 しかし、それらはすべて、作曲の適用レベルで機能し、作曲中の作曲セットを独断的に扱います。 構成アプローチの重要な改善点は、既存の構成からメタ構成を適用することで新しい構成を取得できることです。 このトピックは興味深いものです。誰もそれに触れることはありませんが、次回はそれについて詳しく説明します。 私はあなたを退屈させなかったと思います。
以上が私の研究の主題です。 私はすぐに、同じGCDアルゴリズムのように、または計算の割合が無視できるプロジェクトで、単純な計算に使用するための合成アプローチが提案されていないことを述べます。 コミュニティが信じていることを本当に知りたいです。 組成アプローチには未来がありますか? 作曲を練習しますか? このためのツールが必要ですか?
PS突然、作曲のテーマに触れた最近の投稿を見ました。 それらが互いに補完することを望みます。
PPS記事の修正を手伝ってくれたsekrasoftに感謝します。