内容
パート1:はじめに。
パート2:GPUハードウェアと並列通信パターン。
パート3:基本的なGPUアルゴリズム:削減、スキャン、およびヒストグラム。
パート4:基本的なGPUアルゴリズム:コンパクトなセグメントスキャン、並べ替え。 いくつかのアルゴリズムの実用化。
パート5:GPUプログラムの最適化。
パート6:逐次アルゴリズムの並列化の例。
パート7:並列プログラミング、動的並列処理の追加トピック。
免責事項
この部分は主に理論的なものであり、実際には必要ないでしょう。これらのアルゴリズムはすべて、多くのライブラリに長い間実装されています。
ステップ数(ステップ)vs操作数(作業)
多くのHabr読者は、アルゴリズムの実行時間を推定するために使用される大きなO表記法におそらく精通しているでしょう。 たとえば、 マージソートアルゴリズムの実行時間はO(n * log(n))と推定できると言われています。 実際、これは完全に正しいわけではありません。1つのプロセッサを使用する場合のこのアルゴリズムの操作時間または操作の総数はO(n * log(n))と推定できると言う方が正しいでしょう。 明確にするために、アルゴリズム実行ツリーを検討します。

したがって、 n個の要素の並べ替えられていない配列から始めます。 次に、2つの再帰呼び出しが行われ、配列の左半分と右半分がソートされます。その後、ソートされた半分がマージされ、 O(n)操作で実行されます。 ソートされた部分のサイズが1になるまで再帰呼び出しが実行されます-1つの要素の配列は常にソートされます。 これは、ツリーの高さがO(log(n))であり、 O(n)操作が各レベルで実行されることを意味します(第2レベルで、 Oで2回のマージ(n / 2) 、第3レベルで、 Oで4回のマージ( n / 4)など)。 合計-O(n *ログ(n))操作。 プロセッサが1つしかない場合(プロセッサはCPUではなく抽象的なプロセッサを指します)、これはアルゴリズムの実行時間の推定値でもあります。 ただし、 いくつかのハンドラーと一緒になんらかの方法でマージを並列に実行できると仮定します -せいぜい各レベルでO(n)操作を分割して、各ハンドラーが一定数の操作を実行するようにします-その後、各レベルがOに対して実行されます( 1)時間、およびアルゴリズム全体の実行時間の推定値はO(log(n))に等しくなります !
簡単に言えば、ステップ数はアルゴリズム実行ツリーの高さと等しくなります(同じレベルの操作が互いに独立して実行できる場合-したがって、標準形式では、マージソートアルゴリズムのステップ数はO(log(n))と等しくありません-同じレベルの操作は独立)、しかし操作の数-操作の数:)したがって、GPUでプログラミングするときは、操作の総数を増やしても、より少ないステップでアルゴリズムを使用するのが理にかなっています。
次に、3つの基本的な並列プログラミングアルゴリズムの異なる実装を検討し、ステップ数と操作数の観点からそれらを分析します。
畳み込み(削減)
畳み込み演算は、要素の配列に対して実行され、畳み込み演算子によって決定されます。 畳み込み演算子は、 バイナリおよび連想でなければなりません。つまり、2つの要素を入力として受け取り、等式a * (b * c)=(a * b) * cを満たします 。ここで、 *は演算子指定です(可換性プロパティa * b =と混同しないでください) b * a )。 要素の配列a 1 、...、a nに対する畳み込み演算は、 (...((a 1 * a 2 ) * a 3 )... * a n )として定義されます 。 畳み込み演算を実装するための逐次アルゴリズム実行ツリーの形式は次のとおりです。
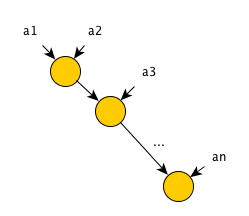
明らかに、このアルゴリズムでは、操作の数はステップの数に等しく、 n-1 = O(n)に等しくなります。
「並列化」アルゴリズムに考慮畳み込み演算子の結合性の性質を取るために十分であり、再配置ブラケット場所:(...((1 * 2)* 3)... * N)=( 1 * 2)*( a 3 * a 4 ) * ... * (a n-1 * a n ) 。 つまり、値(a 1 * a 2 ) 、 (a 3 * a 4 )などを同時に計算し、結果の値に対して畳み込み演算を実行できます。 そのようなアルゴリズムの実行ツリー:
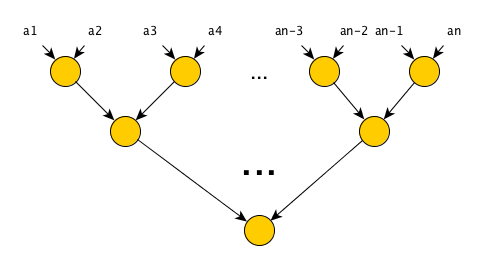
現在、ステップ数はO(log(n))に等しく、操作数はO(n)であり、これは朗報です-括弧の単純な順列により、操作数は同じままで、ステップ数が大幅に少ないアルゴリズムが得られました!
スキャン
スキャン操作も要素の配列に対して実行されますが、スキャン演算子とアイデンティティ要素によって決定されます 。 スキャン演算子は、畳み込み演算子と同じ要件を満たしている必要があります。 ユニット要素には、プロパティI * a = aが必要です 。ここで、 Iはユニット要素、 *はスキャン演算子、 aはその他の要素です。 たとえば、加算演算子の場合、乗算演算子-1の場合、単位要素は0になります。要素a 1 、...、a nの配列にスキャン操作を適用した結果は、同じ次元nの配列になります。 スキャン操作には2つのタイプがあります。
- スキャンを含む-結果は次のように計算されます: [reduce([a 1 ])、reduce([a 1 、a 2 ])、...、reduce([a 1 、...、a n ])] - iの代わりに出力配列のi番目の入力要素は、 i番目の要素自体を含む以前のすべての要素の畳み込み演算を適用した結果になります 。
- 排他的スキャン-結果は次のように計算されます: [I、reduce([a 1 ])、...、reduce([a 1 、...、a n-1 ])] -出力配列のi番目の入力要素の代わりにそれは私に番目の要素自体を除くすべての先行要素の畳み込み演算を適用した結果であろう-出力配列の最初の要素は同一要素であろうに。
スキャン操作自体はそれほど有用ではありませんが、多くの並列アルゴリズムの段階の1つです。 あなたの指先で包括的なスキャンの実装があり、排他的なスキャンが必要な場合、配列[a 1 、...、a n ]の代わりに配列[I、a 1 、...、a n-1 ]を渡すだけです。 逆の場合は、配列[a 1 、...、a n 、I]を渡し、結果の配列の最初の要素を破棄します。 したがって、両方のタイプのスキャンは互換性があります。 スキャン操作のシーケンシャル実装のツリーは、コンボリューション操作の実行ツリーと同じに見えます-ツリーの各頂点の直前に、コンボリューションの現在の結果(包括的スキャンの最初の計算の前に1、排他的スキャンのI )を出力配列の対応する位置に書き込みます。
したがって、このようなアルゴリズムのステップと操作の数はn-1 = O(n)に等しくなります。
アルゴリズムのステップ数を減らす最も簡単な方法は非常に簡単です-スキャン操作は本質的に畳み込み操作によって決定されるので、畳み込み操作の並列バージョンをn回だけ開始できないのはなぜですか? この場合のステップ数は実際に減少します-すべての畳み込みは独立して計算できるため、ステップの合計数は最大のステップ数を持つ畳み込み、つまり入力配列全体で計算される最後の畳み込みによって決まります。 合計-O(ログ(n))ステップ。 しかしながら、このようなアルゴリズム踏み込み操作量-最初の畳み込み操作は、第0(除くメモリ動作)を必要- 1、...、最後- n-1個の操作、合計- 1 + 2 + ... + N-1 = (n-1)*(n)/ 2 = O(n 2 ) 。
スキャン操作を実行するための操作アルゴリズムの数の観点から、より効率的な2を検討してください。 最初のアルゴリズムの作成者はDaniel HillisとGuy Steeleです。アルゴリズムの名前はHills&Steele scanです。 アルゴリズムは非常に単純で、python-pseudocodeの6行で記述できます。
def hillie_steele_scan(io_arr): N = len(io_arr) for step in range(int(log(N, 2))+1): dist = 2**step for i in range(N-1, dist-1, -1): io_arr[i] = io_arr[i] + io_arr[i-dist]
または、言い換えると、ステップ0から始まり、ステップlog 2 (N)(小数部を折り畳む)で終わる、各ステップステップで、インデックスiの下の各要素は、値をa [i] = a [i] + a [i-2 ステップとして更新します] (当然、 2 ステップ <= iの場合 )。 頭の中で配列に対するこのアルゴリズムの実行をトレースすると、それが正しい理由が明らかになります。ステップ0の後、各要素にはそれ自体と左側の1つの隣接要素の合計が含まれます。 ステップ1の後-あなた自身と左の3つの隣接要素の合計...ステップn-あなた自身と左の2 n + 1 -1要素の合計-ステップ数がlog 2 (N)の整数部に等しい場合、最後のステップの後に配列が得られることは明らかですスキャンを含む操作の実行に対応します。 アルゴリズムの説明から、ステップ数がlog 2 (N)+ 1 = O(log(n))であることが明らかです。 操作の数は(N-1)+(N-2)+(N-4)... +(N-2 log 2 (N) )= O(N * log(N))です。 8要素の配列とsum演算子の例を使用したアルゴリズム実行ツリーは、次のようになります。
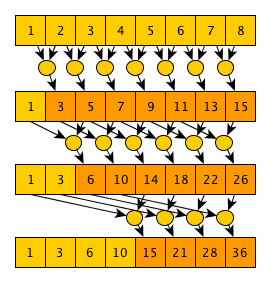
2番目のアルゴリズムの作成者はGuy Blellochで、アルゴリズムは(考えていた人)-Blellochスキャンと呼ばれます。 このアルゴリズムは排他的スキャンを実装し、前のアルゴリズムよりも複雑ですが、必要な操作が少なくなります。 アルゴリズムの主なアイデアは、並列畳み込みアルゴリズムの実装を注意深く見ると、最終値を計算する過程で、たとえば、最初のステップの後、値
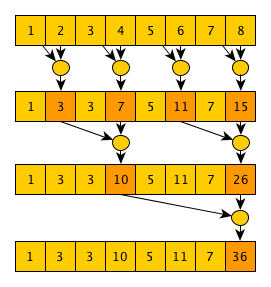
つまり、実際には通常の畳み込みアルゴリズムで、要素
2番目のフェーズは最初のフェーズのほぼ鏡像ですが、2つの値を返す「特別な」演算子が使用され、フェーズの開始時に配列の最後の値が単一要素(加算演算子の場合は0)に置き換えられます。
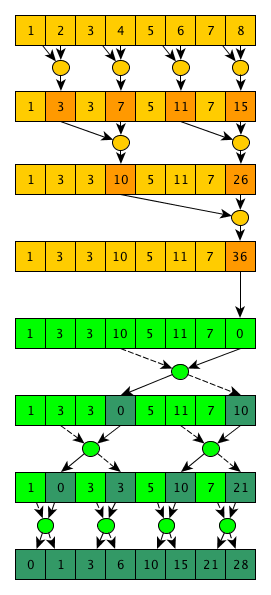
この「特別な」演算子は、左と右の2つの値を取りますが、左の出力値としては単に右の入力を返し、右の出力としてはスキャン演算子を左と右の入力値に適用した結果です。 これらの操作はすべて、計算された中間たたみ込みを最終的に正しく折りたたみ、目的の結果を得るために必要です-入力配列のスキャンを除外します。 このアルゴリズムの図から明らかなように、操作の総数はN-1 + N-1 + N-1 = O(N)であり、ステップ数は2 * log 2 (N)= O(log(N))です。 いつものように、あなたはすべての良い(この場合は改善された漸近性)に支払う必要があります-アルゴリズムは擬似コードでより複雑であるだけでなく、GPUに効率的に実装することもより困難です-アルゴリズムの最初のステップでは、並行して行うことができる多くの作業があります; 第1フェーズの終了時および第2フェーズの開始時に、各ステップで実行される作業はほとんどありません。 そして、第2フェーズの終わりに、各ステップで再び多くの作業を行います(ところで、さらに興味深い並列アルゴリズムには、このような実行パターンがあります)。 この問題の解決策の1つは、2つの異なるコアを作成することです。1つは1つのステップのみを実行し、アルゴリズムの最初と最後に使用されます。 2つ目は、いくつかのステップを連続して実行するように設計され、実行の途中で、つまりフェーズ間の移行時に使用されます。 さて、ホスト側では、現在のステップで実行する必要がある作業量に応じて、今どのカーネルを呼び出すかが決定されます。
ヒストグラム
非公式には、GPUプログラミングのコンテキスト(およびそれだけでなく)のヒストグラムは、セルの配列にわたる要素の配列の分布を指し、各セルには特定のプロパティを持つ要素のみを含めることができます。 たとえば、身長、体重など、バスケットボール選手に関するデータを持っている 身長が180 cm未満、180 cmから190 cm、および> 190 cmのバスケットボール選手の数を知りたいのです。
いつものように、ヒストグラムを計算するためのシーケンシャルアルゴリズムは非常に単純です。配列内のすべての要素を調べて、対応するセルで各要素の値を1ずつ増やします。 ステップと操作の数はO(N)です。
ヒストグラムを計算するための最も単純な並列アルゴリズムは、配列要素の上流で開始することです。各ストリームは、その要素に対してのみセル内の値を増やします。 当然、この場合、アトミック操作を使用する必要があります。 この方法の欠点は速度です。 アトミック操作は、スレッドにセルへのアクセスを同期させ、要素の数が増えると、このアルゴリズムの効率が低下します。
ヒストグラムの構築でアトミック操作の使用を回避する方法の1つは、各ストリームに個別のセルのセットを使用し、これらのローカルヒストグラムを畳み込むことです。 欠点は、スレッド数が多いと、すべてのローカルヒストグラムを格納するのに十分なメモリがない可能性があることです。
最も単純なアルゴリズムの効率を高めるもう1つのオプションは、CUDAの仕様、つまり共有メモリを持つブロックでスレッドを実行することを考慮に入れ、1つのブロック内のすべてのスレッドに対して共通のヒストグラムを作成し、同じアトミック操作を使用してカーネルの最後に追加することですグローバルへのこの棒グラフ。 また、ブロックの一般的なヒストグラムを作成するには、ブロックの一般的なメモリでアトミック操作を使用する必要がありますが、グローバルメモリでのアトミック操作よりもはるかに高速です。
おわりに
このパートでは、多くの並列アルゴリズムの基本的なプリミティブについて説明します。 これらのプリミティブのほとんどの実用的な実装については、次のパートで説明します。ここでは、例としてビット単位のソートを記述します。