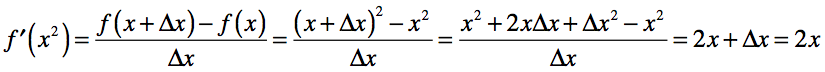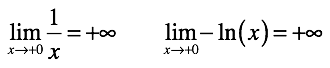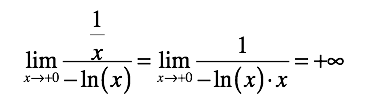ゼロで割ることが標準です。 パート1

パート1.実際、すべてがすでに私たちに分割されています！

パート2.真実は近くにある



彼らは、ゼロによる除算の結果を決定すれば、ゼロで除算できると言います。 代数を展開するだけです。 奇妙な偶然の一致により、少なくともいくつかの、より理解しやすく、簡単なものを見つけるために、そのような拡張の例は不可能です。 インターネットを修正するには、そのような拡張の方法の1つのデモ、またはこれが不可能な理由の説明が必要です。











この記事はトレンドの続きで書かれています：

• お父さん、どうしてゼロで割れないの？
• 本当にしたいのに、なぜゼロで割れないのですか？

免責事項

この記事の目的は、数学の基本的な基礎がどのように機能するかを「人間の言葉」で説明し、知識を構造化し、数学の分岐間の失われた因果関係を復元することです。 すべての推論は哲学的であり、判断は一般に受け入れられているものとは異なります（したがって、数学的厳密さのふりをしません）。 この記事は、読者が「何年も前に塔を通過した」というレベルのために設計されています。



算術、初等、一般、線形代数、数学および非標準分析、集合論、一般的なトポロジー、射影およびアフィン幾何の原理を理解することは望ましいが、必須ではありません。



実験中に、単一の無限が損なわれたわけではありません。

プロローグ

それを超えることは、新しい知識を求める自然なプロセスです。 しかし、すべての検索が新しい知識をもたらすわけではないため、メリットがあります。

1.実際、すべてがすでに私たちに分かれています！

1.1数直線のアフィン拡張

そもそも、おそらくすべての冒険者はゼロで割ることから始めます。 関数グラフを思い出してください 。







ゼロの左側と右側では、関数は「非存在」の異なる方向に進みます。 ゼロ自体には、一般に「渦」があり、何も見えません。



頭で「プール」に突入するのではなく、そこに流れ込むものとそこから流れ出すものを見てみましょう。 これを行うには、 数学的分析のメインツールである制限を使用します 。 主な「トリック」は、制限により、指定されたポイントにできるだけ近づけることができますが、「踏む」ことはできません。 「プール」の前にあるこのような「フェンス」。





オリジナル



さて、「フェンス」セット。 もう怖くない。 「プール」には2つの方法があります。 左側-急な下り、右側-急な登りに行きます。 何人が「フェンス」に行かず、近づかない。 下部と上部の「非存在」を交差させることはできません。 疑いがあります、多分私たちは輪になっていますか？ いいえ、数字は変化しているので、円ではありません。 私たちはまだ数学的分析ツールで胸をruしています。 キット内の「フェンス」の制限に加えて、正と負の無限大があります。 値は完全に抽象的であり（数値ではなく）、形式化されており、すぐに使用できます！ それは私たちに合っています。 「存在」（実数のセット）を、記号付きの2つの無限大で補完します。









数学言語：

この拡張機能を使用すると、引数を無限に設定して制限を取得し、制限を取得した結果として無限を取得できます。



異なる用語を使用して同じことを説明する数学の2つのセクションがあります。



幾何学的な観点から、 数直線のアフィン拡張が実行されます。 つまり、通常の実数のシーケンスは「圧縮」されているため、このシーケンスの境界で操作することができます。 2つの抽象的な無限大の量が境界（条件付き）として導入されます。 拡張子はaffineですが、これはギリシャから来たことを意味するものではなく、ポイント（この場合は数字）の相対的な位置がライン上で保持されることを意味します。 このことから、「より多く」と「より少ない」という関係は、それらの間の数と境界との比較の両方で保持されることになります。



一般的なトポロジの観点から、2つの理想化されたポイント（反対符号の無限大）を追加することにより、数直線の2ポイントのコンパクト化が実行されました。

1.2。数直線の射影拡張

スケジュール通りに歩く 、ゼロへのパスは2つだけです（左と右）。 各パスの最後には小さな「フェンス」があります。 奇妙な偶然の一致により、同じ「フェンス」が「存在」の最下部と最上部にありました。 パスを収束させたい場合は、「フェンス」の背後で、「存在」の一端から他端へのテレポートが必要です。 私たちはすでにそのようなテレポーターを見てきました。 問題ありません。











私たちの先祖がしたように、「存在」の両方の境界線をドッキングしてみましょう。 上記の1次元に移動しましょう。 1次元の線を2次元の平面に表示します。











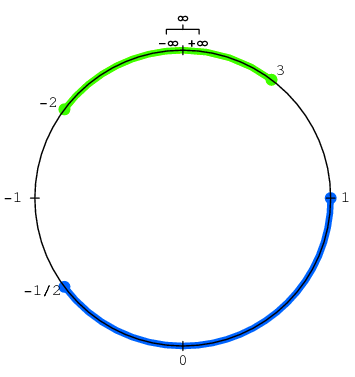
ドッキング後、2つの象徴的な無限の存在はその意味を失います。 代わりに、1つの共通の交点、符号なしの無限大を入力できます。











このドッキングは、太平洋のUTC + 12とUTC-12タイムゾーンの間にある（大部分） 日付線に非常に似ています 。 これが、今日から昨日まで、そして今日から明日までのテレポートの場所です。 非常に小さいものから非常に大きいものへのテレポートがあります。



数学言語：

実際、これは元の実数のセットで実行される独立した拡張です。 この拡張機能は、前述のアフィン拡張機能に基づいていません。



幾何学的な観点から、 数直線の射影拡張が実行されます（ wolfram.comに情報があります ）。 つまり、実際の線の両端を接続する理想的なポイントが導入されます。 拡張子はアフィンではないため、実数と無限大の比較は定義されていません。



一般的なトポロジの観点から、理想化されたポイント（符号なしの無限大）を追加することにより、1行の数直線のコンパクト化が実行されました。



複素数のフィールド上の同様の拡張は、 リーマン球であり 、数学界で広く知られています。

OK、マイナス記号を取り除きました。 ただし、ゼロでは第2種のギャップがあり 、定義上、定義可能なブレークポイントと見なすことはできません。 制限の「有限性」の要件に違反しています。 したがって、左右の限界の平等を判断することはできません。



しかし、無限へのアプローチは同じルールに従って実行されるため、左と右の限界は一致すると言うことができます。 したがって、ギャップを無限にある取り外し可能なギャップのポイントと見なすことができます。



数学言語：

無限に大きい量と小さい量でどのように動作するかを詳しく見てみましょう。 操作では、しばしば下位の小さなものを無視し、結果を記録するときにそれらを単に破棄します。

デリバティブを見つけるときの同様の状況

「小さなもの」を捨てると、情報が失われます！ これは、制限を設定することで明確にわかります。 引数が右側でゼロになる傾向があるため、正の無限大になる傾向がある2つの関数を考えます。

ただし、制限を取った結果の同じ記録は、それらの平等を示していません。 無限大のデータは次数が異なり、これは、ある関数から別の関数への有限な制限がないことによって確認されます。

非標準分析では、このような単純化は受け入れられません。 実数のフィールドは、 超実数を導入することにより拡張されます 。 微小なものは通常の意味の形で表示されます-ゼロですが、投げ出された「小さなもの」全体が付属物に保存されます。 無限に大きな潜在的無限大 （2つまたは1つ-問題ではない）の場合、多くの実際の無限大に分割されます。 一方で、私たちは複雑になります（吸収/無視の可能性を失います）。 一方、私たちは、無限の量と無限の量を比較する能力を獲得しています。 そしてこれは、無限大を数として考えることができることを意味します。



機能用 ゼロの左側と右側の実際の無限大は等しい（モジュロ、つまり符号を考慮しない）

• 両側で、ゼロから無限大までのパス（移動する要素の数）は同じです。
• 近似アルゴリズム（分数式）は同じです。
• アルゴリズムのマイナス記号は、無限に近づく速度や加速に影響しません。

これらの基準は条件付きであり、非標準分析の正式な定義に与えられていないことに注意してください。



さらなる議論のために、実際の無限という概念はもう必要ありません。 私たちは馴染みの世界に戻り、無限の可能性を暗示する無限の概念で動作します。

まあ、制限は同じです。 今では、すべてがそれらの間のギャップを埋める準備ができているようです。









数直線の射影拡張を使用した数学モデルでは、ゼロによる除算が定義されています。









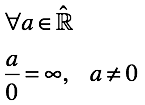
問題は解決したようです。 しかし、急がないで、これがどのような結果をもたらしたか見てみましょう。 除算に加えて、次の操作がシステムで定義されています（無限大は符号なしであることを思い出してください）。









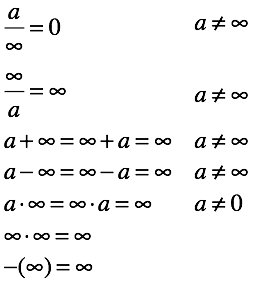
それらのほとんどすべてに追加の条件があり、これは驚くべきことです。 しかし、急がないで、 未定義の操作のリストを見てみましょう：







分布則がどのように動作するかを見てみましょう。 特定の値をそれに代入し、必要な操作を実行します。







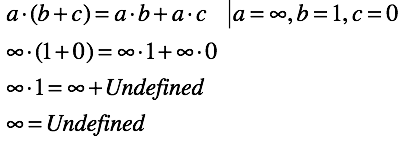
その結果、一部のIDは以前のように動作しなくなります。 しかし、それらは跡形もなく消えませんでした。 分布法則は、右から左にのみ機能します（つまり、等式の右側が定義されている場合）。 これは、否定的な結果の最も明るい例の1つです。 他のアイデンティティは、 多かれ少なかれ安定した形のままでした。



要約すると：

1. アイデンティティの習慣的な行動が変わりました。 それらを操作するには、新しい追加条件を忘れてはなりません。
2. ゼロの習慣的な動作は歪められます。 私たちは推論に慣れています。あなたが何かをゼロ回取ると、ゼロになります。 ただし、この代数システムでは、ゼロと無限大の積は定義されていません。 したがって、変数を含む代数式、たとえばそのようなレコードが発生する 一方的に単純化することはできません。
3. 馴染みのある比較の可能性はなくなります。 多かれ少なかれの比較は、スペースの一部でのみ定義されます。 たとえば、実数と無限大の比較は定義されていません。
4. 結果として得られる代数構造は、一般代数に関しては場ではありません。 流通法に違反しています（上記参照）。 また、無限大の逆要素はありません（この要素と無限大の積は統一性を与えるはずです）。 後者は、無限大を無限大で除算する不確実性の結果と考えることができます。 それでも、これは非常に単純化されていることを理解する必要があります。 逆要素の厳密な定義は、除算演算とは関係ありません。

乾燥残留物中。 古いアプローチは機能しなくなりました。 「if」、「for all but」などのヒープ形式のシステムの複雑さが増しています。 不確実性は1/0と0/0の2つだけでした（電源操作は考慮しませんでした）。5つありました。 1つの不確実性の開示により、さらに多くの不確実性が生じています。

1.2ホイール

符号なしの無限の導入で、すべてが止まりませんでした。 不確実性から抜け出すためには、第二の風が必要です。



そのため、多数の実数と2つの不確実性1/0および0/0があります。 最初を排除するために、数直線の射影拡張を実行しました（つまり、符号なしの無限大を導入しました）。 フォーム0/0の2番目の不確実性に対処してみましょう。 同じことをします。 2番目の不確実性を表す新しい要素で数値のセットを補完します。







除算演算の定義は乗算に基づいています。 これは私たちには合いません。 オペレーション同士のリンクを解除しますが、実数については通常の動作を維持します。 符号「/」で示される単項除算演算を定義します。









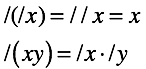
操作を定義します。









この構造は、ホイールと呼ばれます。 この用語は、数直線と点0/0の射影延長の位相的画像との類似性のために取られました。







すべてが良さそうに見えますが、悪魔は詳細にあります：

• ∞またはingにゼロを掛けてもゼロにはなりません。 これは、という事実につながります 一般的な場合。
• ∞およびForの場合、両方の二項演算に逆要素はありません。 つまり、 一般的な場合の乗算。 結果として、空間全体をカバーするバイナリ除算演算を導入する方法はありません。
• 対称加算の状況、 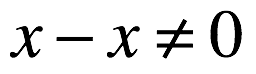一般的な場合。

すべての機能を修正するために、要素のセットを拡張することに加えて、分布法則を記述する1つではなく2つのIDの形でボーナスが適用されます。









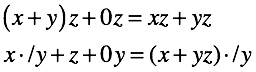
数学言語：

一般代数の観点から、我々は体に作用した 。 そして、ご存知のように、フィールドでは、2つの演算（加算と乗算）のみが定義されています。 除算の概念は、逆、さらに深い場合は単位要素を通じて導出されます。 行われた変更により、加算演算（中立要素としてゼロを使用）と乗算演算（中立要素としてユニティを使用）の両方で、代数システムがモノイドに変わります。



発見者は、シンボル∞および⊥を常に使用するとは限りません。 代わりに、/ 0および0/0の形式でエントリを見つけることができます。

世界はもはやそれほど美しくないのでしょうか？ それでも、急がないでください。 分布法の新しいアイデンティティが拡張セットに対処できるかどうかを確認します 。









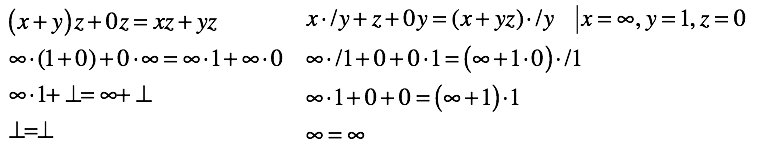
今回は結果がずっと良くなっています。



要約すると：

1. すべての操作は明確に定義されており、「船外に落ちる」方法はありません。
2. 初等代数は車輪の特別な場合です。 アドオン∞とdiscardを破棄すると（つまり、再び そして 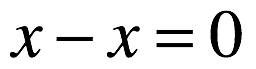）、すべての式はおなじみのものに縮退します。
3. 射影的な拡張子を持つ「定義されていない」すべてのものは、 。 このオブジェクトは、「定義されていない」だけでなく、遭遇するすべてを吸収します。 射影拡大中に不確実性が現れるすべてのギャップは、このオブジェクトによって塞がれました。

乾燥した残留物。 代数はうまく機能します。 しかし、「定義されていない」という概念は基礎としてとられ、彼らはそれを既存のものと見なし、それを操作し始めました。 ある日誰かがすべてが悪いと言うでしょう、そしてあなたはこの「未定義」をさらに「未定義」に分割する必要がありますが、より小さくする必要があります。

このようなものは、 クォータニオンの追加の（jおよびk）虚数単位を仮定しています。



除算を行う他の代数システムがあることに注意してください。 たとえば、「meadows」（一般的な牧草地）。 新しい要素を導入してスペースを拡張しないため、少し簡単です。 目標は、加算および乗算演算の変換、およびバイナリ除算の拒否によって、車輪の両方で達成されます。



「未知のものを動かす」能力は数学の標準です。 しかし、これらのラッパーはすべて、主な質問に対する答えを提供するものではありません。内部には何がありますか？