
ただし、よく知られた堅牢なアルゴリズムの導入は万能薬ではありません。 このアルゴリズムの既製の実装を採用している場合でも、すべての要件などに従って秘密鍵を生成すると、いずれにしても非常に効果的な攻撃にさらされる可能性が残ります。 経験豊富な攻撃者は十分に小さいので、暗号化を回避するための少しの情報は暗号システムとはまったく関係がないように思えます。
私のメッセージは、暗号化ツールの独立した使用を放棄したり、暗号化について考えるたびに毎時1000ドルの給与でコンサルタントを雇うよう説得することではありません。
部分的には、決してリラックスしてはならないことを意味します。攻撃者がシステムに関する詳細情報を取得するために使用できる方法を常に注視する必要があります。また、一部には、Padding Oracle Attackがこのすべてのクールなデモです。 それでは始めましょう。
CBCモード
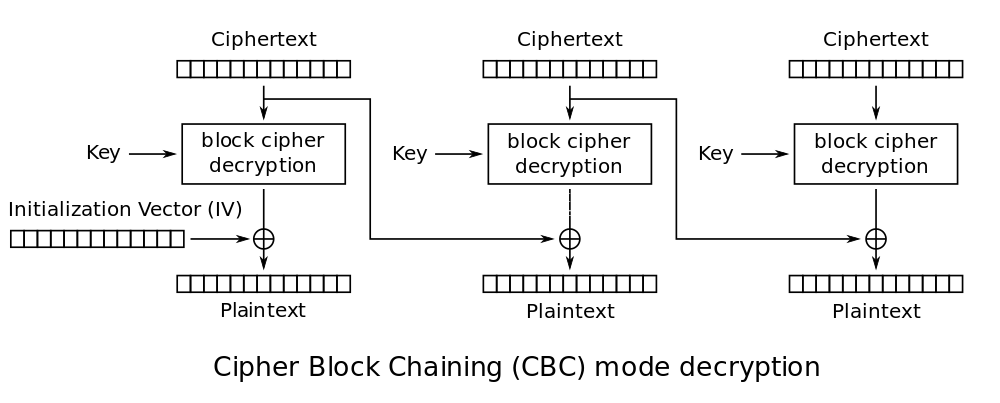
CBC、または暗号ブロックブロッキングモードは、フィードバックメカニズムを使用する対称ブロック暗号化モードの1つです。 これは、暗号化中に、プレーンテキストの次のブロックがブロック暗号化アルゴリズムを通過し、前のブロックの暗号化結果を使用してさらに変更されることを意味します。
したがって、文を暗号化する場合:
これは、慎重に選択された長さの文です。
16バイトの各ブロックの暗号化結果が得られ、プレーンテキストの最後のブロックは特別な方法で補足されます(詳細は後で説明します)。
CBCでは、暗号化アルゴリズムに入る前に、プレーンテキストの各ブロックがビット単位でモジュロ2(xor)を前の暗号文ブロックに追加されます。 このブロックの相互依存性は、各暗号文ブロックがこれまでに処理された各平文ブロックに依存することを意味します。 さらに、平文の任意のバイトが変更されると、暗号文の後続のすべてのバイトが変更されます(なだれ効果)。 ウィキペディアによると、CBCは「Neil FergusonとBruce Schneierが推奨する2つの対称ブロック暗号化モードの1つ」です。
ブロック追加の仕組み(重要!)
暗号文ブロックのパディングの推奨される方法はPKCS7です。 その中で、埋め込まれた各バイトの値は、埋め込まれたバイトの数に等しく設定されます。 したがって、12文字のブロックがある場合、16バイトの標準ブロックサイズまで4バイト[ 04、04、04、04]でパディングされます。 ブロックのサイズが15バイトの場合、1バイト[01]が埋め込まれます。 ブロックのサイズが正確に16バイトの場合、 [16] * 16で構成される新しいブロックを追加します。 (詳細-https://en.wikipedia.org/wiki/Padding_ ( cryptography ) #PKCS7 )
この方法によれば、復号化されたプレーンテキストの最後のブロックは、たとえば[...、13、06、05]で終了できません。 これは、そのような暗号文に変換できる有効な平文がないため、元の暗号文も正しくないことを意味します。
パディングOracle攻撃
暗号文の解読がプレーンテキストで取得され、攻撃者がCBCモードで暗号化に対する攻撃を成功させるのに十分な正しい追加が行われたかどうかの事実を知ることがわかります。 暗号文を何らかのサービスに送信でき、追加が正しいかどうか情報を返す場合、任意の暗号文を開くことができます。
したがって、暗号化を停止するのに十分なエラーは、送信した暗号文が正しい追加で復号化された場合にコード200を返し、そうでない場合にコード500を返すAPIである可能性があります。
これはありそうな状況ではありません。 たとえば、Ruby OpenSSLはこの問題を起こしやすい傾向があります。 公式ドキュメント( http://www.ruby-doc.org/stdlib-1.9.3/libdoc/openssl/rdoc/OpenSSL/Cipher.html#documentation )のサンプルコードを使用するだけで十分です。
decipher = OpenSSL::Cipher::AES.new(128, :CBC) decipher.decrypt decipher.key = "the most secret!" decipher.iv = "also very secret" plain = decipher.update("thewrongpadding!") + decipher.final
このコードは、 OpenSSL :: Cipher :: CipherError:bad decryptをスローします 。これは、インターセプトされない場合、 500エラー応答を返します。
暗号文を盗んだとします。 暗号文を送信し、それらが正しい追加でメッセージに復号化されるかどうかを判断できる場合、盗まれた暗号文を完全に復号化するためにこれをどのように使用できますか?
中間状態
繰り返しになりますが、CBCモードでは、暗号化に入る前に、プレーンテキストの各ブロックが前の暗号化テキストブロックとビット単位のモジュロ2(XOR)で追加されます。 暗号化を解除するとき、各暗号文は復号化プログラムを通過し、前の暗号文ブロックとXORを実行してプレーンテキストを生成します。
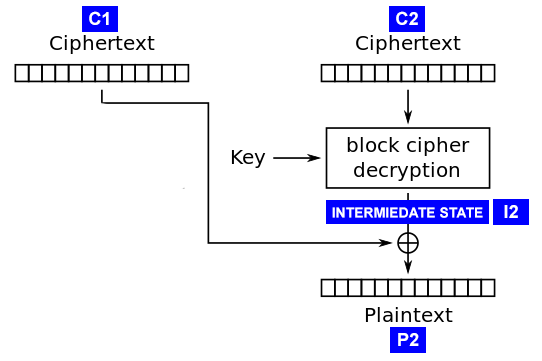
攻撃は、暗号文ブロックごとに復号化手順の「中間状態」(図を参照)を計算することにより機能します。 これは、ブロックアルゴリズムによる復号化後の暗号文ブロックの状態ですが、前の暗号文ブロックとのXORプロシージャの前です。 この状態は、ブロック暗号を経由するのではなく、クリアテキストの下から上昇します。 また、暗号化キーやブロック暗号化アルゴリズムについてもまったく心配しません。
なぜこの中間状態がそれほど重要なのですか? 注:
I2 = C1 ^ P2 P2 = C1 ^ I2
私たちはすでにC1を知っています これは私たちが持っている暗号文の一部です。 したがって、I2が見つかった場合、P2を簡単に見つけてメッセージを解読できます。

暗号文の操作
システムの入力に任意の暗号文を提供できることを思い出してください。サーバーは、復号化後に正しい追加が得られるかどうかを教えてくれます。 この事実を利用するために、 C1 '+ C2を入力に送ります。ここで、 C1'は特別に形成した暗号文ブロックで、 C2は解読したいブロックです。 C1 '+ C2とは、単純な連結(つまり、ブロックの「接着」)を意味します。 復号化の結果をP'2として示します。
まず、 C1 '[1..15]をランダムバイトで埋め、 C1' [16]をゼロ( 0x00 )で埋めます 。 サーバーにC1 '+ C2を渡します。 サーバーがアドオンが正しいと答えた場合、 P2 '[16]が0x01であることを(高い確率で)確認できます(アドオンが正しいため)。 サーバーがエラーで応答する場合は、 C1 '[16]を0x01に設定してから0x02などに設定してメッセージを送信します。 必要な答えが得られるまで。
(翻訳者のメモ。もちろん、次の2つの正解が得られたときに状況が発生する可能性があります。
1)追加01
2)02.02または03.03.03を補足する...
このような状況が発生した場合は、最後から2番目のバイトC1を変更して、操作を繰り返してください。
最悪のシナリオでは、3回の試行が必要になりますが、これはほとんどありません。
)
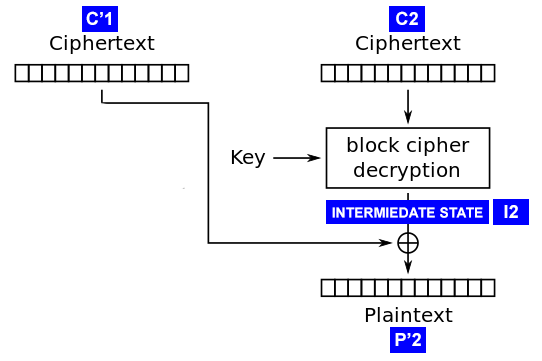
ここで、サーバーがC1 '[16] = 94の 200応答を返したとします。
I2 = C1' ^ P2' I2[16] = C1'[16] ^ P2'[16] = 94 ^ 01 = 95
やった! 中間状態の最終バイトを取得しました。 なぜなら C2は実際の暗号文から取得され、 I2も実際の暗号文と同じです。 したがって、実際のプレーンテキストの最後のバイトを解読できます。
P2[16] = C1[16] ^ I2[16] = C1[16] ^ 95
C1 '[16] = C1 [16]をフィードし、実際のプレーンテキストの最後のバイトを取得します。 この時点では、プレースホルダーが見つかっただけなので、何か面白いものが見つかるまで、プロセスをさらに数回繰り返す必要があります。
続ける
正しい補数が得られるまでC1 'をスクロールして、最後のバイトを見つけました。 この場合、 P'2の最後のバイトは0x01であると結論付けることができます。 次に、 P2 '[16]およびC1' [16]を使用して 、 I2 [16]を見つけます。 このプロセスを続けて、 I2の残りのバイトを見つけ、暗号文ブロック全体を解読します。
C1 '[1..14]をランダムバイトで埋め 、 C1' [15]を0x00に設定し、 C1 '[16]を設定してP2' [16] == 0x02を取得します。
C'1[16] = P'2[16] ^ I2[16] = 02 ^ 95 = 93
これで、 P2 'が0x02で終了することが確実になるため、 P2'が正しい補数を持つ唯一のオプションは、 P2 [16] == 0x02の場合です。 サーバーが200コードを発行するまでC1 '[15]をスクロールします。 これがC1 '[15] == 106で発生したと仮定します。 すでに知っていることを再度行います。
I2 = C1' ^ P2' I2[15] = C1'[15] ^ P2'[15] = 106 ^ 02 = 104
そして出来上がり! I2の最後から2番目のバイトを知っています。 したがって、以前に行ったように、 P2の最後から2番目のバイトを見つけることができます。
P2[15] = C1[15] ^ I2[15] = C1[15] ^ 104
C2の 16バイトすべてについても同様です。
その他のブロック
暗号文ブロックの形状は、それらと前のブロックのみに依存します。 したがって、上記のアルゴリズムを暗号文の各ブロックに(最初のブロックとは別に)適用できます。 最初のブロックは初期化ベクトル( IV )を使用して暗号化され、 IV自体は暗号化手順中にランダムに選択されます。 IVを認識するまで、最初のブロックを解読することはできません。IVの明白な値[0,0,0、...]の愚かな列挙を除き、ここで考えられることはありません。合理的な平文。 そして、最初の16バイトが「 Dear Eugene! 」のようなものになることを期待してそうしてください。
これがすべてPadding Oracle Attackです。
それが、暗号に関連するすべてが怖い理由です。
暗号化プリミティブは独立して実装すべきではなく、すでに発明されたものの上にシステムを構築していることを知っています。 専門家によって開発された強力な暗号の背後に隠れると、リラックスした気分になります。 そして、私たちは鍵を秘密にし、どこにでも開いたテキストを残さない一方で、私たちは無敵だと感じます。
しかし、今見たように、最小のサードパーティチャネルである情報のドロップは、システムを完全に脆弱にするのに十分です。 私たちの想像上の開発者は、既存のライブラリから永続的なアルゴリズムを使用し、必要な長さのキーを生成し、一時的な値( nonce )を再利用するような愚かなことはしませんでした。 彼の唯一の間違いは、非自明な例外をキャッチしなかったことであり、それにより、暗号文が解読されて正しいものになったかどうかを理解する機会が得られました。
もちろん、例外をキャッチし、1つのIPアドレスからのリクエスト数を制限し、疑わしいリクエストを監視することで、特にこの攻撃を防ぐことができますが、これはポイントではありません。 攻撃者は常に洗練されており、実装のわずかな欠陥さえ使用します。 信頼できるソースから取得した場合でも、暗号化には注意してください。
ありがとう
Matasano Crypto Challenges( http://matasano.com/articles/crypto-challenges/ )。暗号化に興味を持ちました。 私はそれを強くお勧めします!
_____
ロバート・ヒートンの記事の著者の許可を得て行われた翻訳。
ソース: http : //robertheaton.com/2013/07/29/padding-oracle-attack/
より興味深い関連リンク:
https://class.coursera.org/crypto-preview/lecture/38