
良い一日、親愛なるhabrasociety。
今日は、数学的なパラドックスのような魅力的なトピックに触れたいと思います。 ハブに関するこのトピックに関するいくつかの素晴らしい記事がすでに公開されています(1、2、3、4、5)が、数学ではこの選択による興味深いパラドックスは尽きることがありません。
したがって、ここではまだ適切な報道を受けていない他の面白いパラドックス(および「完全ではない」パラドックスの一部)を検討しようとします。
ヒープのパラドックスとBalげたパラドックス
これらのパラドックスは古代から知られています。 まず、「ヒープ」の概念の不確実性に関連するヒープパラドックスを定式化し、検討します。

「グレインを1つのグレインに追加すると、ヒープはどの時点で形成されますか?」
または逆の言葉遣い:
「100万粒のヒープから1粒を除去し、いつからヒープでなくなるのか?」
パラドックスの定式化は、1つの穀物がヒープを形成しないという明白な前提と、束ではない集団への1つの穀物の追加がヒープの形成に不可欠ではないという誘導的前提に基づいています。 これらの仮定から、任意の多数の穀物の集合体がヒープを形成することはありません。これは、穀物のヒープの存在の概念と矛盾します。 明らかに、これらの考慮事項は誤った結論につながります。
しかし、ごく最近まで、ここでどのような推論を使用するのかが明確ではありませんでした。 Lofti Zadehによるファジィ集合の理論とファジィ論理の出現によってのみ、ファジィ論理の古典的なオブジェクトである「束であること」という曖昧な概念があるため、ファジィ推論がここで適切であることが明らかになりました。 ファジーロジック内のこれらのオブジェクトは、何らかのファジーセットによって特徴付けられる不正確な値を持つものとして解釈されます。
そのような推論によれば、各ステップでの結論は同じままですが、その正当性の帰属は各ステップで減少します。 この所属が50%を下回ると、反対の結論がより正確になります。
同様の推論を「ハゲ」パラドックスに適用できます。
「頭の毛が一度に1本落ちる場合、人はいつからはげますか?」
嘘つきのパラドックス

絵の中の声明が真である場合、その内容に基づいて、それは偽であることが真実です。 しかし、それが偽であれば、それが主張するものは偽です。 それは、図の中の文が偽であることは真実ではないことを意味し、それはこの文が真実であることを意味します。
嘘つきのパラドックスは、口語的な発話と形式的な論理の間の矛盾を示し、真と偽の両方の声明を紹介します。 正式な論理の枠組みの中で、この声明は証明可能でも議論の余地もありません。したがって、このパラドックスに対する解決策はありませんが、それを排除するためのさまざまなオプションがあります。
このため、前のセクションで使用した推論を適用できます。これは、ステートメントが0.5で真であると仮定し、0.5で偽である、つまり、すべてのフレーズが完全に偽または完全に真であるとは限りません絵の中にあるが、何らかの方法で-真実を伝える”
トリプルロジックを使用しても同じ結論に達することができます。 「真実」、「偽」、「無期限」の3つの真実があります。 「無期限」とは、真実と虚偽の中間的な意味を意味します。 真実のこの程度に、嘘つきのパラドックスを含めてください。
すでに述べたように、これは嘘つきのパラドックスの解決策ではなく、このパラドックスが発話の古典的な2値論理で生じる理由の単なる説明です。 彼らは、この場合、すべてのステートメントを真と偽に厳密に分割することは逆説につながるため、適用できないことを証言しています。
現時点では、多くの人がこの見解を固守しており、この声明はまったく論理的な声明ではなく、形式論理の古典的な方法を適用することは無意味です。
テセウスのパラドックス
このパラドックスは次のように定式化できます。

「元のオブジェクトのすべてのコンポーネントが置き換えられた場合、オブジェクトは同じオブジェクトのままですか?」
このパラドックスに対するいくつかの解決策が提案されています。 アリストテレスの哲学派によると、オブジェクトを説明するいくつかの理由があります:物の形、物質、本質(アリストテレスの教えによれば、それは最も重要な特性です)。 これから進んで、船は本質を変えず、摩耗した材料だけが変わったので、船は同じままでした。
次の決定では、「同じ」議論に定量的および定性的特性を与えることが提案されました。 この場合、ボードを変更した後、テセウスの船は量的に同じであり、質的には別の船になります。
最近、テセウスのパラドックスを解決するために、3次元の船も4次元時間の長さを持つ4次元解釈を使用することが提案されました。 結果として得られる時系列にわたる4次元の船は、それ自体と量的に同じです。 ただし、個々の「タイムスライス」は、質的に異なる場合があります。
アビリーンの逆説

このパラドックスは、各個人が自分の目標がグループの目標に反していると考え、したがって気にしないという事実のために、人々のグループがグループのメンバーの可能な選択と矛盾する決定を下すことができるということです。
パラドックスは、アビリーンパラドックスと他の管理に関する瞑想でジェリーハーベイによって説明されました。 この名前は、この記事で説明されている次の逸話に基づいてパラドックスに付けられています。
あるテキサスの暑い夜、ある家族がポーチでドミノをし、義父が昼食のためにアビリーンに行くことを申し出た。 妻は言った:「それはいいですね。」 夫は、旅行が長く暑いと約束したという事実にもかかわらず、他の人に適応する必要があると考え、こう言いました。 お母さんが拒否しないことを願っています。」 私の義理の母は答えました:「もちろん、行こう! 私はアビリーンに長い間行っていません。」
道は暑く、ほこりっぽく、長い。 彼らがようやくカフェテリアに到着したとき、食べ物は無味でした。 4時間後、彼らは疲れきって家に帰った。
そのうちの一人は不誠実に言った:「旅行が良かったのは本当ですか?」 私の義理の母はこれに、実際、彼女は家にいるほうがいいと言いましたが、他の3人は熱意に満ちていたので、彼女は行くでしょう。 夫は言った:「私はどこにも行かないことを嬉しく思います、私は残りの喜びを与えるためだけに行きました。」 妻は言った:「そして、私は他の人の喜びを頼りに行った。 自発的にこの旅行に行くには夢中にならなければなりませんでした。」 義父は、残りは退屈だと思ったからと言って、これを提案したと答えた。
そして、彼らは誰も望んでいない旅行に行ったという事実にfact然として座っていました。 彼らのそれぞれは、その日をむしろ穏やかに楽しむでしょう。
このパラドックスはさまざまな社会科学によって簡単に説明されており、人は自分のグループの行動に反することはめったにしないことが確認されています。 私は、多くの人がこのパラドックスに出会ったことがあると思います。
シンプソンのパラドックスとウィルロジャースの現象
これらのパラドックスは「見かけ上」、つまり直感的なレベルで発生する可能性があることに注意してください。ただし、計算を行うと、パラドックスが発生しないことを簡単に確認できます。
シンプソンのパラドックスを説明するために、有名な数学の普及者であるMartin Gardnerが説明した例を考えてみましょう。
石が4セットあるとします。 セットNo. 1の黒い石を引き出す確率は、セットNo. 2よりも高くなります。また、セットNo. 3から黒い石を引き出す確率は、セットNo. 4よりも大きくなります。セットNo. 1とセットNo. 3を組み合わせますセット番号2-セット番号4(セットII)。 直感的に、セットIから黒い石を引く確率はセットIIよりも高くなると予想できます。 ただし、一般的な場合、このようなステートメントは偽です。
シンプソンのパラドックスが満たされる例:
| 黒いボール | 白いボール | 黒い石を引き出すチャンス | |
|---|---|---|---|
| セット番号1 | 6 | 7 | 6/13≈0.4615 |
| セット番号2 | 4 | 5 | 4/9≈0.4444 |
| セット番号3 | 6 | 3 | 6/9≈0.6667 |
| セット番号4 | 9 | 5 | 9/14≈0.6429 |
次に、黒い石をより高い確率で引き出すことができるセットNo. 1とNo. 3と、黒い石を低い確率で引き出すことができるNo. 2とNo. 4を混合します。
| 黒いボール | 白いボール | 黒い石を引き出すチャンス | |
|---|---|---|---|
| セットI | 12 | 10 | 12/22≈0.5454 |
| セットII | 13 | 10 | 13/23≈0.5652 |
混合後の表からわかるように、セットIIから黒い石を引き出す確率はセットIからよりも高かった。
数学的には、セットの全体的な可能性は両方の色に対する黒い石の数の比率に依存するため、ここにはパラドックスはありません。この場合、4つのセットには9つの黒い石があり、最初の7つには7つの白い石があり、それが最終的なレイアウトに最も影響を与えました。
シンプソンのパラドックスとウィルロジャースの現象に近い。 実際、彼らは同じ現象を異なる用語で記述しています。
私は何度もこのようなフレーズに出くわしたと思います:
「オークがオクラホマを出てカリフォルニアに移動したとき、両州の平均知能が向上しました。」
このフレーズはウィルロジャースに起因するものであり、この現象に敬意を表してこの現象が名付けられました。
数学の観点からは、ここにも矛盾はありません。 これを検証するには、最初のセットが{1、2}で、2番目のセットが{90,100}である2つのセットを考慮するだけで十分です。数値90が2番目のセットから最初のセットに転送される場合、最初のセットと2番目のセットの両方の要素の算術平均は増加します。
細胞の消失
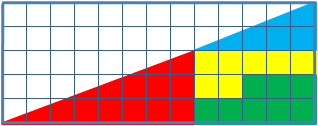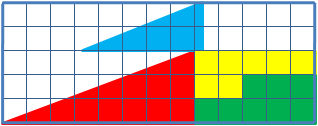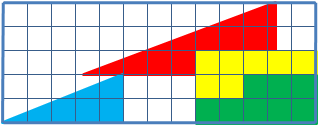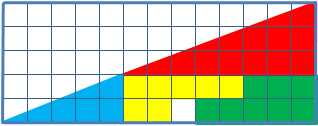
洗練された兆候を伴う図の再配置のための幅広いクラスのタスク:最初は、マスクされたエラーがその状態に導入されました。 ある程度、これらのタスクは数学よりも目の錯覚に近いものです。
たとえば、1つの同様の問題を考えてみましょう。4つの部分で構成される13×5セルの長方形の三角形を考えます。 パーツの再配置後、初期の比率を視覚的に維持しながら、パーツによって占有されていない追加のセルが表示されます。
数学的には、パラドックスはなく、この地域の神秘的な消失はありません。 実際、視覚的に観察される三角形はそのようなものではなく、両方の疑似三角形の斜辺は実際には破線です(最初の三角形では内側にねじれがあり、2番目では外側にねじれがあります)。 互いの上に三角形を置くと、「欠けている」領域を含む「斜辺」の間に平行四辺形が形成されます。
結論の代わりに
残念なことに、1つの記事の枠組み内ですべての興味深い数学的パラドックス(および「完全ではない」パラドックス)を検討することは不可能です。 しかし、この記事があなたを無関心なものにしないことを願っています。読み物を無駄にしないと決めたなら、私はとてもうれしいです。