Fortran 90方言で記述しますが、GNU拡張（同じ倍精度の数値）を使用します。
少しのフラクタル理論
フラクタル （ fractus-押しつぶされた、壊れた、壊れた）-狭い意味で、自己相似性の特性を持つ複雑な幾何学的図形、つまり、それぞれが全体として全体の図形に似ているいくつかの部分で構成されています。
フラクタルの大規模なグループがあります-代数的フラクタル。 この名前は、このようなフラクタルを構築する原理に基づいています。 それらを構築するには、再帰関数を使用します。 たとえば、代数フラクタルは次のとおりです。ジュリアセット、マンデルブロセット、ニュートンプール（フラクタル）。
代数的フラクタルの構築
構築方法の1つは、反復計算です。
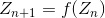どこで 
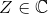、そして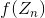 
いくつかの機能。 この関数の計算は、特定の条件が満たされるまで続きます。 この条件が満たされると、ドットが表示されます。
複素平面の異なる点に対する関数の動作は、異なる動作を持つことができます。
- 無限に向かう
- 0になる傾向
- いくつかの固定値を受け入れ、それらを超えません。
- 混behaviorとした行動。 傾向がない
代数的フラクタルを構築するための最も単純な（理解と実装の両方のための）アルゴリズムの1つは、「 エスケープ時間アルゴリズム 」として知られています 。 つまり、複素平面の各点の数を繰り返し計算します。
それが証明されています
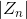よりベイルアウトであることが判明し、シーケンス 
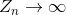。 比較 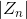救済を使用すると、セットの外側にあるポイントを見つけることができます。 セットの外側にあるポイントの場合、シーケンス 
無限になりませんので、 救済に達することはありません。
2つの単純なフラクタル、ジュリアセットとマンデルブロセットを検討します。 それらは同じ関数に従って計算されますが、定数のみが異なります。ジュリアの場合は定数定数であり、マンデルブロブの場合、定数は複素平面上の点に依存します。
ジュリアセットの構築
プログラムの開始と終了は簡単で簡単です。
program frac end
次に、いくつかの定数を導入する必要があります。
INTEGER, PARAMETER :: iterations = 2048 ! . , REAL(8), PARAMETER :: mag_ratio = 1.0_8 ! REAL(8), PARAMETER :: x0 = 0.0_8 ! REAL(8), PARAMETER :: y0 = 0.0_8 ! INTEGER, PARAMETER :: resox = 1024 ! INTEGER, PARAMETER :: resoy = resox REAL(8), PARAMETER :: xshift = (-1.5_8 / mag_ratio) + x0 ! REAL(8), PARAMETER :: yshift = (-1.5_8 / mag_ratio) + y0 ! REAL(8), PARAMETER :: CXmin = -1.5_8 / mag_ratio ! REAL(8), PARAMETER :: CXmax = 1.5_8 / mag_ratio ! resox x resoy REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox ! REAL(8), PARAMETER :: CYmin = -1.5_8 / mag_ratio REAL(8), PARAMETER :: CYmax = 1.5_8 / mag_ratio REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy COMPLEX(8), PARAMETER :: c = DCMPLX(0.285_8, 0.01_8) !
そして、ここで何かを説明する必要があります。 REALおよびCOMPLEXは、単精度浮動小数点数と2つのREALで構成される複素数です。 REAL（8）は倍精度数であり、 COMPLEX（8）はそれぞれ2つのREAL（8）で構成される複素数です。 文字Dも標準関数に追加され（ ABSの場合と同様）、倍精度数の使用を示します。
次に、いくつかの変数を導入する必要があります。
CHARACTER, DIMENSION(:), ALLOCATABLE :: matrix ! COMPLEX(8) :: z INTEGER :: x, y, iter REAL(8) :: iter2 ! ALLOCATE(matrix(0 : resox * resoy * 3))
ALLOCATABLEを使用する必要があります！ なぜなら そうでなければ：
CHARACTER, DIMENSION(0:resox * resoy * 3) :: matrix !
スタックに割り当てたメモリ。これは、複数のスレッドで使用する場合は受け入れられません。 したがって、ヒープにメモリを割り当てます。
だから私は二次元配列を使わない ヒープに割り当てられると、配列はより多くのスペースを占有し、ファイルに書き込むのがより難しくなります。
次に、OpenMPによって生成されるスレッドの数を指定する必要があります。
call omp_set_num_threads(16)
そして、計算は直接始まります。 Fortranでは、OpenMPのディレクティブはコメントを介して指定されます（C / C ++では、このための特別なマクロ#pragmaがあります）。
!$OMP PARALLEL DO PRIVATE(iter, iter2, z) do x = 0, resox-1 do y = 0, resoy-1 iter = 0 ! z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) ! Z do while ((iter .le. iterations) .and. (CDABS(z) .le. 4.0_8)) ! bailout 2, 4, .. z = z**2 + c iter = iter + 1 end do iter2 = DFLOAT(iter) - DLOG(DLOG(CDABS(z))) / DLOG(2.0_8) ! iter-log2(ln(|Z|)) matrix((x + y * resox) * 3 + 0) = CHAR(NINT(DMOD(iter2 * 7.0_8, 256.0_8))) ! matrix((x + y * resox) * 3 + 1) = CHAR(NINT(DMOD(iter2 * 14.0_8, 256.0_8))) matrix((x + y * resox) * 3 + 2) = CHAR(NINT(DMOD(iter2 * 2.0_8, 256.0_8))) end do end do !$OMP END PARALLEL DO
最も時間のかかる部分は終わりました。 さらに、情報を知覚に便利な形式、つまり画像で表示することも残っています。 PNM形式を使用します。 これが最も簡単な画像形式です。
PNMはいくつかのセクションで構成されています。
P6 # 1024 1024 255
最初の行は、ピクセル情報を記録するための形式を示しています。
- P1 / P4-白黒画像
- P2 / P5-グレー画像
- P3 / P6-カラー画像
最初のPは、ピクセルの色がASCII文字で書き込まれるオプションであり、2番目のPは、ピクセルの色をバイナリ形式で記録することを可能にします（ディスクスペースを大幅に節約します）。
次の行はコメントで、画像の解像度とピクセルあたりの色数です。 色数の後に、ピクセルに関する情報が直接表示されます。
画像をファイルに書き始めます。
open(unit=8, status = 'replace', file = trim("test.pnm")) write(8, '(a)') "P6" !(a) write(8, '(a)') "" write(8, '(I0, a, I0)') resox, ' ', resoy write(8, '(I0)') 255 write(8, *) matrix close(8) DEALLOCATE(matrix)
プログラムを終了しても、OSは使用中のメモリをシステムに返すため、良識のためにDEALLOCATEを実行します。
プログラムをビルドするには、GNUコンパイラ-gfortranを使用できます。
gfortran -std=gnu frac.f90 -o frac.run -fopenmp
次の画像が表示されます。
1024x1024 
マンデルブロ集合を生成する方法
これは簡単で、 cを置き換えていくつかの定数を変更するだけです。 この場合、定数cを削除し、変数cを追加します。
COMPLEX(8) :: z, c
z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) ! Z c = z
また、古い定数も変更します。
INTEGER, PARAMETER :: MAIN_RES = 1024 INTEGER, PARAMETER :: resox = (MAIN_RES / 3) * 3 INTEGER, PARAMETER :: resoy = (resox * 2) / 3 REAL(8), PARAMETER :: xshift = (-2.0_8 / mag_ratio) + x0 REAL(8), PARAMETER :: yshift = (-1.0_8 / mag_ratio) + y0 REAL(8), PARAMETER :: CXmin = -2.0_8 / mag_ratio REAL(8), PARAMETER :: CXmax = 1.0_8 / mag_ratio REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox REAL(8), PARAMETER :: CYmin = -1.0_8 / mag_ratio REAL(8), PARAMETER :: CYmax = 1.0_8 / mag_ratio REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy
次の画像が表示されます。
1023x682 
更新した
Adaで働いた後、1つのエラーが見つかりました-Modを使用しました。 この機能は私にとって松葉杖の役割を果たしました。 0〜255の値を取るカラーチャンネルがあります。値が最大値を超えないようにModを実行したことがわかりました。 画像を見るとわかるように、これにより色が急激に変化します。
この式を使用してこれを修正します。
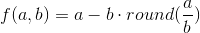。 線形空間での線形補間のバリエーションが判明します。
使いやすくするために、次の関数を作成します。
function myround(a) result(ret) REAL(8), intent(in) :: a INTEGER :: ret ! b 255, INTEGER . ret = ABS(INT(a - 255.0_8 * NINT(a / 255.0_8))) !NINT() round() C, .. end function myround program frac INTEGER :: myround
そして、色の割り当てをドットに置き換えます：
matrix((x + y * resox) * 3 + 0) = CHAR(myround(iter2 * 7.0_8)) matrix((x + y * resox) * 3 + 1) = CHAR(myround(iter2 * 14.0_8)) matrix((x + y * resox) * 3 + 2) = CHAR(myround(iter2 * 2.0_8))
次の画像が取得されます。
1024x1024 
upd2
なぜなら FortranおよびAdaでは、EOLが自動的に選択されますが、Unix以外のPNMシステムでは間違っていることがわかります。 これを回避するには、次の自転車を使用する必要があります。
write(8, '(a, a, $)') "P6", char(10) write(8, '(a,$)') char(10) write(8, '(I0, a, I0, a, $)') resox, ' ', resoy, char(10) write(8, '(I0, a, $)') 255, char(10) write(8, *) matrix
中古文学
en.wikipedia.org/wiki/Fractal
en.wikipedia.org/wiki/Julia_set
en.wikipedia.org/wiki/Mandelbrot_set
en.wikipedia.org/wiki/OpenMP
openmp.org/wp/openmp-specifications
gcc.gnu.org/onlinedocs/gfortran