😤 🍇 🍥 永続キュー 😺 ☪️ 😂

最近の出版物「暗黙のキーによる永続的なデカルトツリー」に触発されて、永続キューの実装について書くことにしました。通常のキューは些細な構造であるため、その永続バージョンは非常に単純であるはずであると考えた人たちは、彼らは間違っていて、結果として生じる実装は、少なくとも上記のツリーの場合ほど簡単ではありません。

問題の声明

もちろん、いわゆる完全永続性を実装します。これは、中間バージョンが読み取り専用モードだけでなく、いつでも要素を追加および抽出できることを意味します。さらに、もちろん、非永続的なオプション、つまりO（n）の場合と同じ動作時間と追加のメモリの漸近的な動作が必要です。ここで、nはキューで実行される操作の総数です。ところで、要件をO（n log n）に緩和すると、キューは暗黙的なキーを持つ永続的なデカルトツリーを使用して簡単にエミュレートされます。

次の簡単なインターフェースを使用して、データ構造を操作します。キューの結果のバージョンには、負でない整数で番号が付けられます。最初は、番号0の空のキューのみです。キューのNバージョン（元の空を含む）に、0からの番号が付けられていますN-1に変更すると、次の4つのクエリを完了することができます。

empty（query_id）-指定された番号のキューが空かどうかを確認します。
front（query_id）-キューの最初の要素を返しますが、キュー自体はまったく変更されず、新しいキューは作成されません。キューが空でない場合、操作は有効です。
push（query_id、new_element）-元の新しい要素の末尾に追加することで取得した、番号Nの下に新しいキューを作成します。古いバージョンはquery_idで引き続き使用できます。
pop（query_id）-元から最初の要素を抽出することで取得した、番号Nで新しいキューを作成します。元のキューは古い番号で引き続き利用できます。元のキューが空だった場合、新しいキューも空になります。

スタックを使用したキューのシミュレーション

すべての問題に対して、簡単で、速く、間違った解決策があります。

-オンライン裁判官の第一法則

ご存知のように、永続スタックは非常に単純なデータ構造であり、その漸近的な動作が必要です。さらに、2つのスタックを使用してキューをシミュレートできることもわかっています。明らかなアイデアがあります。これらの2つのスタックを永続化して、問題を解決します。残念ながら、このような単純なアプローチは機能しません。問題は、このシミュレーションでは、すべての操作に漸近線O（1）があるわけではないということです：pop'e中に要素を取得するスタックが空になった場合、別のスタックからすべての要素を転送します。通常のキューの場合、各要素は1回だけシフトされるため、漸近的な振る舞いの合計はO（n）のままですが、永続的な場合、各要素は多くのキューに属し、それに応じて数回シフトされます。たとえば、qをこのスタックが空のキューの番号とし、受信したキューのpush（q、1）およびpush（q、2）の後、このスタックは空のままになり、キューの各要素がシフトされますq 2回。配置された要素の共同使用を整理することは、それらをシフトすることによって得られるスタックの最下位の要素が異なる（それぞれ1および2）ため、各要素がその下の要素へのポインタを格納するように配置されるため、不可能です。したがって、いずれの場合も、対応する最後を示す最後から2番目の要素のコピーが2つ必要になります。したがって、チェーン内の目的の最後から2番目を示すために最後から2番目のコピーが必要になります。。

それでも、そのような考えに基づいたアルゴリズムがあり（2つのスタックを使用してキューをシミュレート）、pop'eから取得したスタックが空にならないことを保証し、6つのスタックを使用してこれを保証します。私のアルゴリズムはこのアイデアを明示的に使用していませんが、一般的な点についてはもちろんあなたはそれを見つけることができます。

アルゴリズムの説明

永続スタックを実装するときと同じ構造を使用してみましょう：追加された要素をツリー（より正確には、ツリー-フォレストのセット）の形で保存します。各頂点には、追加された要素とキューの前の要素（より正確には、対応する要素）へのポインターがあります前の要素はツリーの最上部です）。キュー要素の将来について言えば、要素に対応する頂点を意味することがよくあります。

この場合の空でないキューは、キューの最初と最後の要素へのポインターのペアで表すことができ、最初の要素に対応する頂点は、必ず最後に対応する頂点の祖先になります（1つの要素のキューの場合は、一致します）。そのような構造とその中のキューの表示の例：

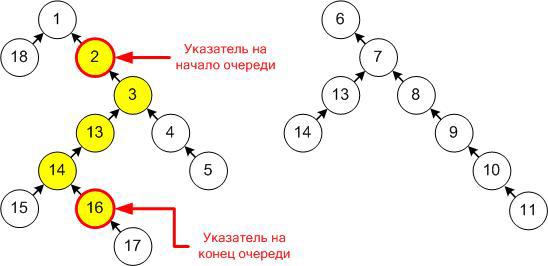
プッシュ操作は単に新しい頂点を作成し、元のキューの最後の要素の親として設定します（または空のルートに追加された場合は新しいルートになります）。ポップ操作はフォレストにまったく触れず、単に最初の要素にポインターを移動します。したがって、作成後、頂点は作業が終了するまで変更されないため、新しい操作が既存のキューを台無しにすることを心配する必要はありません。

このアプローチの唯一の問題は、ポップ操作の実装です（他の3つは簡単です）。最初の要素にポインターを移動する頂点を決定する方法は明確ではありません。複数のピースが存在する可能性があり、それらのすべてが格納されている場合でも、それらのどれがキューの次の要素に対応するかは完全に不明です。したがって、3つ以上の要素が存在する各キューに対して、単純に接続されたリストの要素へのポインターを追加で保存します。ポインターによるリスト要素には、キューの2番目の要素へのポインターと、リスト内でその下にある要素、3番目へのポインターが含まれます。 4番目など。初期キューへのこのようなポインターがあると、ポップを実行するときに、キューの新しいヘッドを簡単に特定できるようになります。結果のキューのリスト項目へのポインターは、このリストの次の要素へのポインターにすぎません。

ただし、2つのスタックによるキューのエミュレーションが機能しない理由と同様の理由で、リストの下の各キューの中間頂点が完全にすべてであることを保証するために、成功しません。次に、それらの最初、そしてこのリストが小さくなり始めたら、新しいリストを作成し、ステップごとに移動します（つまり、プッシュまたはポップ操作ごとに構築中のリストを1要素ずつ増やします）。私たちの木のピークの親にしかし、古いリストが完了した時点に維持しようと、我々はすでに新しいアラートを持っていました。

より正式には、キューごとに、開始と終了へのポインタと完成したリストの要素へのポインタに加えて、構築中のリストの要素へのポインタも保存し（何も作成しない場合は0になります）、新しい値を計算します次の単純なアルゴリズムを使用したキュー（元のpush'aまたはpop'aへの適用後に受信）：

最初のキューのこのポインターが0に等しい場合、新しいリストの作成を開始する時間であるかどうかを確認します（このような確認の基準は以下で説明します）
- 時間が経過したら、リスト内の次の項目へのヌルポインターを使用してリストアイテムを作成し（これにより、作成されたアイテムが作成済みリストの最後になります）、ポインターをキューの最後から2番目の要素（最後のアイテムの親）の先頭に配置し、
- まだ時間がない場合は、ポインターをゼロのままにします。
ゼロ以外のソースポインターの場合、リストを1要素上に展開します。リスト内の次の頂点としてソースを指し、このソース要素に対応する親を指す新しい要素を作成します。

同時に、最初のキューに保存されているソースリスト要素自体またはそれへのポインターを変更せず、一般に、すべてのデータ（ツリートップ、リストアイテム、キューに保存されているデータ）は不変です（つまり、作成後）意味が変わることはありません）。すべてがどのように機能し、push'eまたはpop'eで何が起こるかを示す図が図に表示されています（理解しやすくするために、どんなに頑張っても機能しませんでした）。

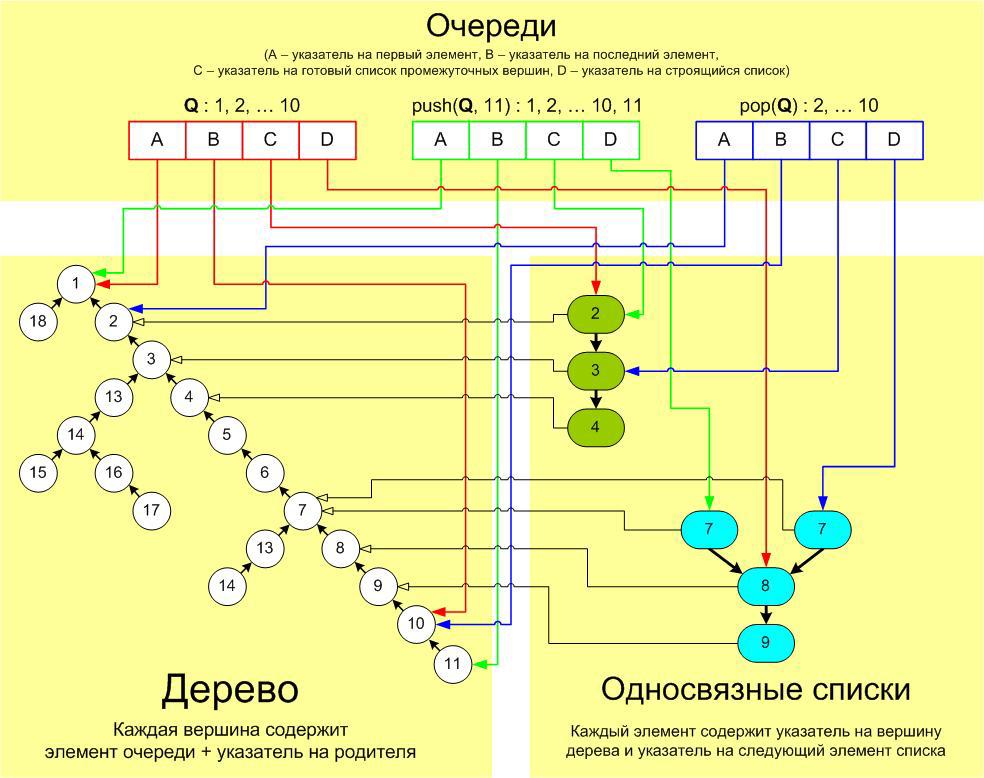
したがって、リストの完了時に最初の中間要素に到達すると、このキューの構築が完了します（他のいくつかのキューはこのリストを完了し続ける可能性がありますが、古い要素は決して変わらないため、これは決して害を与えません）。この場合、古いリストの要素へのポインタの代わりに、新しいリストの要素へのポインタを記述し、構築されたリストへのポインタをゼロに割り当てます。

アルゴリズムの説明から、各リクエスト中にツリーの新しい頂点を1つと新しいリストアイテムを1つだけ作成し、O（1）時間、つまり求めた漸近的な動作を費やし、正しいことを議論するだけであることがわかります基準。

建設開始時のチェック基準

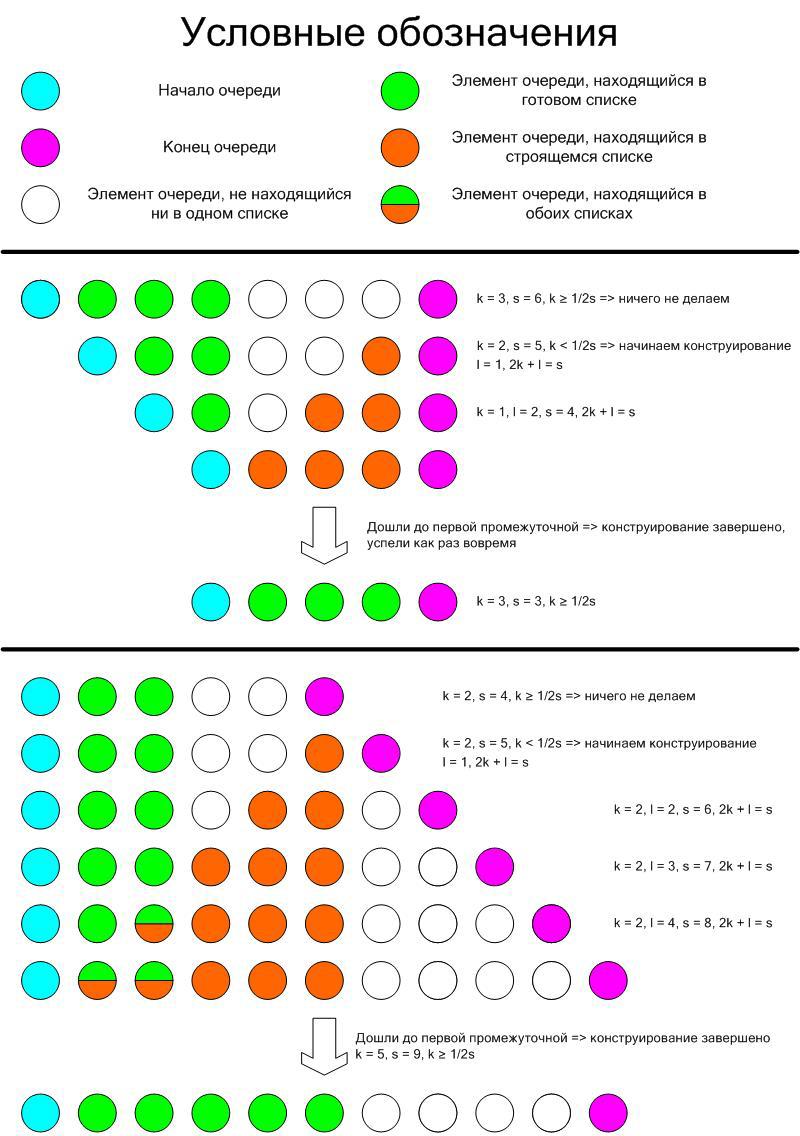
リストのサイズが中間頂点（つまり、最初と最後のない頂点）の数の1/2以上である間は、何もせず、リストが小さくなるとすぐに新しいリストの作成を開始します。中間の頂点がない場合、不等式0≥0があり、何もしないことに注意してください。つまり、特別な場合、これは必要ありません。このアプローチでは、古いリストが終了し、新しいリストがまだ準備されていない状況で自分自身を見つけることができないことを証明します。

まず、次の不変式を証明します。新しいリストを作成する場合、各ステップで2k + l = s、kは古いリストの要素数、lは作成されたリスト（このステップで作成が完了した後）にあり、sは中間リストの総数です要素。数学的帰納法で証明します。構築を開始したばかりの最初のステップを考えます（l = 1）。ただし、新しいキュー2k-s <0（基準）では、元の2k _old -s old≥0であることに注意してください。これがどのように発生するかを見てみましょう。 + 1、ポップの場合、k = k _old -1およびs = s _old -1.ご覧のとおり、どちらの場合でも2k-sは2k _old -sだけ1 _古いです。両方の違いは整数です。、2番目の要素は0、1番目の要素は-1です。したがって、2k + 1 = sであり、lは1です。誘導ベースが証明されています。移行を証明しましょう：いくつかの構築ステップで2k _old + l _old = s _oldにします。次に、l = l _old + 1（1要素でリストを完成）、push'aの場合：k = k _old 、s = s _old + 1、pop'aの場合：k = k _old -1、s = s _old -1.どちらの場合も、平等が成立します。つまり、ステートメントが証明されます。

ポップ操作を実行していて、必要なリストがソースキューで空であると仮定します（プッシュする場合、このリストは一切使用しません）。次に、次の2つのいずれかがあります。

または、最初のキューについては、新しいリストの作成を開始しなかったため、このキューには2k≥sがあり、

k = 0 => s =0。これは、サイズ0、1、または2のキューであり、pop'aを完了するための最後の要素が十分であることを意味します。
不変2k + l = s、k = 0 => l = s≠0 =>のおかげで、開始されてからl≠0になり、構築されたリストは空ではなく、すべての中間要素を含んでいました。空でないリストを取得します。

構築が完了したときに、構築の欠如の条件が満たされていること、つまり、結果のリストの長さが中間頂点の総数の1/2以上であること、つまり、完了時に2l≥s、または同等にl≥s -l。しかし、s-lとは何ですか？これは、リストにない中間頂点の数です。これは、構築プロセス中に発生したプッシュ操作の数に等しいことを理解するのは簡単です。ただし、このような各操作では、リスト内の要素の数も1ずつ増加します（前の手順で、作成されたリストの要素がキューの3番目の要素に対応してポップし、新しいキューの場合、リスト要素は最初の中間要素に対応するようになります。、ただし、これは構築の最後のステップでのみ可能で、ポップ操作でのみ可能です。したがって、l≥そのようなプッシュの数（厳密にそれ以上であることを理解することは難しくありません）。これを証明する必要がありました。

明確にするために、次の2つの極端なケースで何が起こるかを示します。常にポップするときと、常にプッシュするときです。

C ++実装

最後に、上記のデータ構造をC ++で実装します（実装ではC ++ 11の革新を使用します）。このコードをプロトタイプとして使用する価値はあります。できるだけシンプルで短く、他のすべてを犠牲にしてそれを満足させるようにしようとしました。

persistent_queue.h

#ifndef PERSISTENT_QUEUE_H #define PERSISTENT_QUEUE_H #include <cstdlib> #include <vector> using Element_type = int; class Persistent_queue { public: Persistent_queue(); ~Persistent_queue(); Persistent_queue(const Persistent_queue&) = delete; Persistent_queue& operator =(const Persistent_queue&) = delete; using Queue_id = size_t; static const Queue_id start_queue_id = 0; Queue_id push(Queue_id queue_id, const Element_type& value); Queue_id pop(Queue_id queue_id); const Element_type& front(Queue_id queue_id); size_t size(Queue_id queue_id); bool empty(Queue_id queue_id); private: struct TreeNode; struct QueueIntermediateTreeNodeList; struct Queue { const TreeNode* const first; const TreeNode* const last; const size_t size; const QueueIntermediateTreeNodeList* const known_intermediate_list; const QueueIntermediateTreeNodeList* const constructing_intermediate_list; const bool own_last; const bool own_known_intermediate_list; Queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list); ~Queue() = default; Queue(Queue&& source) = default; // needed for vector reallocation Queue(const Queue&) = delete; Queue& operator =(const Queue&) = delete; }; std::vector<Queue> queues_; Queue_id register_new_queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list); void manage_intermediate_lists(const QueueIntermediateTreeNodeList*& known_intermediate_list, const QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const TreeNode* const first, const TreeNode* const last, const size_t size); }; #endif // PERSISTENT_QUEUE_H

persistent_queue.cpp

 #include "persistent_queue.h" #include <cassert> struct Persistent_queue::TreeNode { const TreeNode* const parent; const Element_type element; TreeNode(const TreeNode* const parent, const Element_type& value) : parent(parent), element(value) {} ~TreeNode() = default; TreeNode(const TreeNode&) = delete; TreeNode& operator =(const TreeNode&) = delete; }; struct Persistent_queue::QueueIntermediateTreeNodeList { const Persistent_queue::TreeNode* const front; const QueueIntermediateTreeNodeList* const next; const size_t size; QueueIntermediateTreeNodeList(const Persistent_queue::TreeNode* const front, const QueueIntermediateTreeNodeList* const tail_list) : front(front), next(tail_list), size{tail_list ? tail_list->size + 1 : 1} { assert(front); } ~QueueIntermediateTreeNodeList() = default; QueueIntermediateTreeNodeList(const QueueIntermediateTreeNodeList&) = delete; QueueIntermediateTreeNodeList& operator =(const QueueIntermediateTreeNodeList&) = delete; }; Persistent_queue::Queue::Queue( const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size, const Persistent_queue::QueueIntermediateTreeNodeList* const known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list ) : first(first), last(last), size(size), known_intermediate_list(known_intermediate_list) , constructing_intermediate_list(constructing_intermediate_list) , own_last(own_last), own_known_intermediate_list(own_known_intermediate_list) { // Some asserts if (size == 0) { assert(first == nullptr); assert(last == nullptr); } else { assert(first); assert(last); if (size > 1) assert(last->parent); } if (size <= 2) { assert(known_intermediate_list == nullptr); assert(constructing_intermediate_list == nullptr); if (size == 1) assert(first == last); if (size == 2) assert(first == last->parent); } else { assert(known_intermediate_list); assert(first == known_intermediate_list->front->parent); } } size_t Persistent_queue::size(const Persistent_queue::Queue_id queue_id) { return queues_.at(queue_id).size; } bool Persistent_queue::empty(const Queue_id queue_id) { return size(queue_id) == 0; } const Element_type& Persistent_queue::front(const Persistent_queue::Queue_id queue_id) { assert(!empty(queue_id)); return queues_.at(queue_id).first->element; } Persistent_queue::Queue_id Persistent_queue::register_new_queue(const TreeNode* const first, const TreeNode* const last, const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list, const QueueIntermediateTreeNodeList* const constructing_intermediate_list, const bool own_last, const bool own_known_intermediate_list) { queues_.emplace_back(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); return queues_.size() - 1; } Persistent_queue::Persistent_queue() { register_new_queue(nullptr, nullptr, 0, nullptr, nullptr, false, false); } Persistent_queue::~Persistent_queue() { for (const auto& q : queues_) { if (q.own_last) delete q.last; if (q.own_known_intermediate_list) delete q.known_intermediate_list; delete q.constructing_intermediate_list; } } Persistent_queue::Queue_id Persistent_queue::push(const Persistent_queue::Queue_id queue_id, const Element_type& value) { const auto& queue_for_push = queues_.at(queue_id); const size_t size = queue_for_push.size + 1; const bool own_last = true; const TreeNode* first; const TreeNode* last; if (queue_for_push.size == 0) { first = last = new TreeNode(nullptr, value); } else { first = queue_for_push.first; last = new TreeNode(queue_for_push.last, value); } bool own_known_intermediate_list; const QueueIntermediateTreeNodeList* known_intermediate_list = queue_for_push.known_intermediate_list; const QueueIntermediateTreeNodeList* constructing_intermediate_list = queue_for_push.constructing_intermediate_list; manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list, own_known_intermediate_list, first, last, size); return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); } Persistent_queue::Queue_id Persistent_queue::pop(const Persistent_queue::Queue_id queue_id) { const auto& queue_for_pop = queues_.at(queue_id); const bool own_last = false; const TreeNode* first; const TreeNode* last; size_t size; const QueueIntermediateTreeNodeList* known_intermediate_list; if (queue_for_pop.size <= 1) { first = last = nullptr; size = 0; known_intermediate_list = nullptr; } else { last = queue_for_pop.last; size = queue_for_pop.size - 1; if (queue_for_pop.size == 2) { first = queue_for_pop.last; known_intermediate_list = nullptr; } else { assert(queue_for_pop.known_intermediate_list != nullptr); first = queue_for_pop.known_intermediate_list->front; known_intermediate_list = queue_for_pop.known_intermediate_list->next; } } bool own_known_intermediate_list; const QueueIntermediateTreeNodeList* constructing_intermediate_list = queue_for_pop.constructing_intermediate_list; manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list, own_known_intermediate_list, first, last, size); return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list, own_last, own_known_intermediate_list); } void Persistent_queue::manage_intermediate_lists( const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size) { own_known_intermediate_list = false; const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0); size_t known_intermediate_list_size = (known_intermediate_list ? known_intermediate_list->size : 0); if (2*known_intermediate_list_size < intermediate_nodes_count) { auto try_to_replace_known_to_constructing = [&](){ if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) { known_intermediate_list = constructing_intermediate_list; known_intermediate_list_size = constructing_intermediate_list->size; constructing_intermediate_list = nullptr; return true; } return false; }; if (!try_to_replace_known_to_constructing()) { const auto adding_node = (constructing_intermediate_list ? constructing_intermediate_list->front->parent : last->parent); constructing_intermediate_list = new QueueIntermediateTreeNodeList( adding_node, constructing_intermediate_list); if (try_to_replace_known_to_constructing()) own_known_intermediate_list = true; } } // Check invariants if (2*known_intermediate_list_size >= intermediate_nodes_count) assert(constructing_intermediate_list == nullptr); const size_t constructing_intermediate_list_size = (constructing_intermediate_list ? constructing_intermediate_list->size : 0); const auto invariant_sum = 2*known_intermediate_list_size + constructing_intermediate_list_size; assert(invariant_sum >= intermediate_nodes_count); if (constructing_intermediate_list) assert(invariant_sum == intermediate_nodes_count); }

TreeNode、Queue、およびQueueIntermediateTreeNodeListタイプは、アルゴリズムのツリーの最上部、キュー、および単純に接続されたリストの要素に対応します。 Queueのブール変数は、クラスのデストラクタでメモリを正しく解放するために使用されます：ツリーの頂点とリストアイテムは、それらを作成したキューによって削除されます（上記のように、各リクエストで頂点は1つだけ、リストアイテムは1つだけ作成されます）。ツリーの最上部は、プッシュ操作中にのみ作成され、それへのポインタはそれぞれ最後に書き込まれます。own_lastは、新しい頂点と古い頂点のどちらが最後に書き込まれるかを示します。作成中に作成されたリストアイテムは、ほとんどの場合、constructing_intermediate_listに書き込まれます。ただし、作成され、同じステップでの作成が完了した場合は例外です。そのような場合。

2番目の明白でない可能性のあるポイントは、プライベートメンバー関数manage_intermediate_listsで、次のようになります。

 void Persistent_queue::manage_intermediate_lists( const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list, const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list, bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last, const size_t size) { own_known_intermediate_list = false; const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0); size_t known_intermediate_list_size = (known_intermediate_list ? known_intermediate_list->size : 0); if (2*known_intermediate_list_size < intermediate_nodes_count) { auto try_to_replace_known_to_constructing = [&](){ if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) { known_intermediate_list = constructing_intermediate_list; known_intermediate_list_size = constructing_intermediate_list->size; constructing_intermediate_list = nullptr; return true; } return false; }; if (!try_to_replace_known_to_constructing()) { const auto adding_node = (constructing_intermediate_list ? constructing_intermediate_list->front->parent : last->parent); constructing_intermediate_list = new QueueIntermediateTreeNodeList( adding_node, constructing_intermediate_list); if (try_to_replace_known_to_constructing()) own_known_intermediate_list = true; } } // Check invariants }

この関数は、構築中のリストへのポインターを操作するための上記のアルゴリズムを実装します（最初の3つのパラメーターは非定数リンクを介して渡されます。最初の2つのパラメーターについては、呼び出しの前に必要な値によって変数が初期化されると想定されています）。古い要素が最初の中間体になっている場合、リストを完成する前に確認することが重要です。すでに述べたように、ポップの場合、このオプションは可能です。誰かが建設の開始基準を常にチェックしていることに気付いたのかもしれません。

 if (2*known_intermediate_list_size < intermediate_nodes_count) {

建設がすでに進行中の場合は、個別に強調せずに。事実は、設計プロセス全体を通して基準が真のままであるということです。これは明らかに、設計不変式：2k + l = s、l> 0 => 2k <sから得られます。

可能な最適化

まず、図でわかるように、構築が進行中の同じキューで複数の異なる操作が実行されると（図ではこれらはポップ（Q）およびプッシュ（Q、11）操作です）、いくつかの要素はまったく同じですリスト（ツリーの同じ次の要素と同じ頂点を指します-ダイアグラムには、番号7の2つの青い円があります）。たとえば、完了時に、誰かがすでに自分の前でそれを行っているかどうかを示す構造を使用して、そのような要素を1つに「接着」しようとすることができます（そのような構造として、通常のベクトルまたは二重にリンクされたリストを使用できます）。明らかに、このような最適化は、高度に分岐したツリーの場合にうまく機能します（多くのメモリを節約します）。

第二に、別の重複があります：完成したリストと作成中のリストの要素がツリーの同じ頂点を指している場合（この写真では緑とオレンジの要素について話している）。もちろん、このような重複を完全に回避することはできません。リストの開始と継続が同じである可能性が高いためですが、作成中のリストの最初が完成したリストの最後（キューの先頭ではなく）に達すると、単に「接着」することができますこれにより、少しのメモリが節約されます。残りのリスト（もちろん、この準備に対応）については、複製する必要があります。したがって、この最適化は、木に長い直線の枝がたくさんある場合に最もよく現れます。

最後に、第三に、定数で遊んでみることができます。たとえば、1つの要素ではなく1つのステップで完了することができますが、2ずつでは、k <1/3秒で構築を開始するだけで十分です。おそらく何らかの形で役立つでしょう。

それを読んだすべての人に感謝します。

永続キュー