
実際、プログラムを実行する前に、Pythonインタープリターはすべての部分を特別なバイトコードにコンパイルします。 SkidanovAlexハブユーザーによって記述された方法を使用して、このデコレーターは結果の関数バイトコードを分析し、そこで使用されるアルゴリズムを最適化しようとします。 さらに、この最適化はプログラムを特定の回数ではなく漸近的に加速できることがわかります。 したがって、ループ内の反復回数が多いほど、最適化された関数は元の関数に比べて加速される回数が増えます。
この記事では、デコレーターがこのような最適化をいつどのように管理するかについて説明します。 このデコレータを含むcpmoptimizeライブラリを自分でダウンロードしてテストすることもできます。
理論
2年前、 SkidanovAlexは、次の操作をサポートする制限された言語インタープリターを説明する興味深い記事を公開しました。
# x = y x = 1 # x += y x += 2 x -= y x -= 3 # x *= 4 # loop 100000 ... end
言語の変数の値は数値である必要があり、そのサイズは制限されていません( 長い演算がサポートされています)。 実際、変数はPythonの整数として保存され、数値がハードウェアでサポートされている4バイトまたは8バイトタイプの境界を超えると、長い算術モードに切り替わります。
長い演算が使用されない場合を考えてください。 その場合、操作の実行時間は変数の値に依存しません。つまり、ループではすべての反復が同時に実行されます。 このようなコードを従来のインタープリターのように「額」で実行すると、サイクルは時間内に完了します
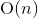 ここで、 nは反復回数です。 つまり、 n回の反復のコードが時間tで機能する場合、次のコードは
ここで、 nは反復回数です。 つまり、 n回の反復のコードが時間tで機能する場合、次のコードは 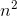 繰り返しは時間とともに機能します
繰り返しは時間とともに機能します 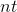 ( 計算の複雑さを参照)。
( 計算の複雑さを参照)。
元の記事のインタープリターは、特定のマトリックス形式の変数を使用して各言語でサポートされている操作を示し、変数の元の値を持つベクトルに乗算します。 乗算の結果として、変数の新しい値を持つベクトルを取得します。
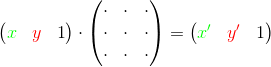
したがって、一連の操作を実行するには、ベクトルに次の操作に対応する行列を行列で乗算する必要があります。 別の方法-結合性を使用して、行列を最初に互いに乗算し、次に結果の積によって元のベクトルを乗算することができます。

ループを完了するには、 n-ループ内の反復回数、およびマトリックスB-ループの本体からの操作に対応するマトリックスの連続積を計算する必要があります。 次に、元のベクトルに行列Bを n回掛ける必要があります。 別の方法-最初に行列Bをn乗し、次にベクトルに結果を乗じることができます:
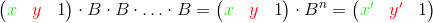
バイナリべき乗アルゴリズムを使用すると、サイクルをはるかに短い時間で完了することができます
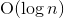 。 したがって、 n回の反復のコードが時間tで機能する場合、
。 したがって、 n回の反復のコードが時間tで機能する場合、 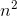 繰り返しは時間とともに機能します
繰り返しは時間とともに機能します 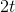 (前のケースのように、2倍だけ遅く、 n倍遅くはありません)。
(前のケースのように、2倍だけ遅く、 n倍遅くはありません)。
その結果、上で書かれたように、サイクルnの反復回数が大きくなるほど、最適化された関数が加速する回数が増えます。 したがって、最適化の効果は、 nが大きい場合に特に顕著になります。
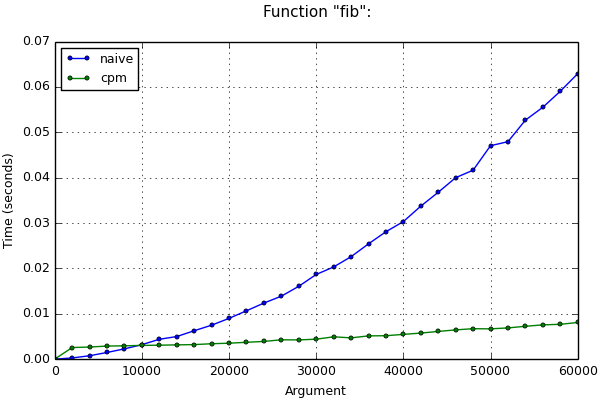
長い算術演算がまだ使用されている場合、上記の時間推定は正しくない場合があります。 たとえば、 n番目のフィボナッチ数を計算するとき、反復から反復までの変数の値はますます大きくなり、それらを使用した操作は遅くなります。 この場合、プログラムの実行時間の漸近的な推定を行うことはより困難です(各反復で変数の数値の長さと、数値の乗算に使用される方法を考慮する必要があります)。ここでは説明しません。 それでも、この最適化手法を適用すると、この場合でも漸近的な動作が改善されます。 これは、チャートにはっきりと表示されます。
アイデア
数十年前にプログラマーがプログラム内の変数に4を掛ける必要がある場合、彼は乗算演算を使用しませんが、同等の高速処理-左に2ビットシフトします。現在、コンパイラー自体がこのような最適化を行うことができます。 開発時間を短縮するための努力の中で、高レベルの抽象化を備えた言語、新しい便利なテクノロジー、およびライブラリーが登場しました。 プログラムを書くとき、開発者はほとんどの時間をコンピューターにプログラムが何をすべきかを説明し(数字に4を掛ける)、効果的な方法ではありません(ビットシフトを使用)。 したがって、効率的なコードを作成するタスクは、コンパイラーとインタープリターに部分的に転送されます。
コンパイラは、さまざまな操作をより効率的な操作に置き換えたり、式の値を予測したり、コードの一部を削除または交換したりできるようになりました。 しかし、コンパイラはまだ、人が書いた計算アルゴリズムを漸近的により効率的なアルゴリズムに置き換えていません。
元の記事で説明した方法の実装は、実際のプログラムで使用するには問題があります。このためには、コードの一部を特別な言語で書き換える必要があり、このコードとやり取りするには、インタープリターでサードパーティのスクリプトを実行する必要があります。 ただし、この記事の著者は、コンパイラーの最適化において実際に彼のベストプラクティスを使用することを提案しています。 Pythonプログラムを最適化するために、実際のプロジェクトでの使用に本当に適した形式でこのメソッドを実装しようとしました。
私が書いたライブラリを使用する場合、最適化を適用するには、高速化する必要がある関数の前に、特別なデコレータを使用して1行追加するだけで十分です。 このデコレータは、可能であれば独立してサイクルを最適化し、いかなる状況でもプログラムを「中断」しません。
使用例
デコレータが役立つ便利なタスクをいくつか考えてみましょう。
例1 長いサイクル
図に示されているルールに対応するシーケンスがあり、そのn番目の項を計算する必要があるとします。
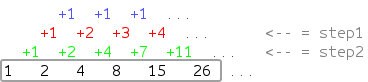
この場合、シーケンスの次のメンバーがどのように表示されるかは直感的にわかりますが、それに対応する数式を見つけて証明するには時間がかかります。 それでも、ルールを記述する簡単なアルゴリズムを記述し、コンピューター自体が問題の答えをすばやく読む方法を見つけ出すことを提案できます。
from cpmoptimize import cpmoptimize, xrange @cpmoptimize() def f(n): step1 = 1 step2 = 1 res = 1 for i in xrange(n): res += step2 step2 += step1 step1 += 1 return res
興味深いことに、この関数を
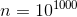 、とのループ
、とのループ 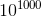 繰り返し。 最適化がなければ、このような関数は考えられる期間動作を終了しませんでしたが、デコレーターを使用すると、正しい結果を返しながら1秒もかかりません。
繰り返し。 最適化がなければ、このような関数は考えられる期間動作を終了しませんでしたが、デコレーターを使用すると、正しい結果を返しながら1秒もかかりません。
例2 フィボナッチ数
n番目のフィボナッチ数を迅速に計算するために、行列を累乗するという同じ考えに基づいた高速でありながら重要なアルゴリズムがあります 。 経験豊富な開発者であれば、数分で実装できます。 そのような計算が実行されるコードがすぐに機能する必要がない場合(たとえば、1万未満の数値でフィボナッチ数を計算する必要がある場合)、作業時間を節約するために、開発者はほとんどの場合、労力を節約してソリューションを記述することを決定します額。」
それでもプログラムをすばやく動作させる必要がある場合は、努力して複雑なアルゴリズムを記述するか、デコレータを関数に適用して自動最適化方法を使用する必要があります。 nが十分に大きい場合、どちらの場合もプログラムのパフォーマンスはほぼ同じになりますが、2番目の場合、開発者は自分の作業時間よりも少ない時間を費やします。
小さいnと大きいnの表とグラフで、以下で説明するメソッドの実行時間を比較できます。
公平を期すために、フィボナッチ数を計算するための高速2倍化と呼ばれる別のアルゴリズムがあることに注意してください。 不必要な数の加算と乗算が除外されているため、彼は以前のアルゴリズムにやや勝ちました。 このアルゴリズムの計算時間も、比較のためにグラフに表示されます。
グラフ 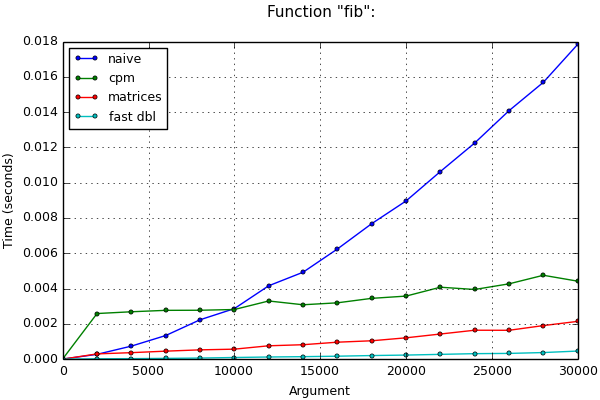
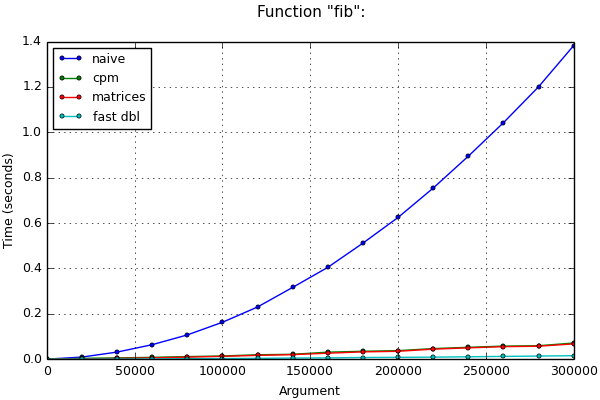


時間の結果
Function "fib": (*) Testcase "big": +--------+----------+--------------+--------------+--------------+-------+ | arg | naive, s | cpm, s | matrices, s | fast dbl, s | match | +--------+----------+--------------+--------------+--------------+-------+ | 0 | 0.00 | 0.00 | 0.00 | 0.00 | True | | 20000 | 0.01 | 0.00 (2.5x) | 0.00 (3.0x) | 0.00 (5.1x) | True | | 40000 | 0.03 | 0.01 (5.7x) | 0.00 (1.8x) | 0.00 (4.8x) | True | | 60000 | 0.06 | 0.01 (7.9x) | 0.01 (1.4x) | 0.00 (4.8x) | True | | 80000 | 0.11 | 0.01 (9.4x) | 0.01 (1.3x) | 0.00 (4.6x) | True | | 100000 | 0.16 | 0.01 (11.6x) | 0.01 (1.1x) | 0.00 (4.5x) | True | | 120000 | 0.23 | 0.02 (11.8x) | 0.02 (1.2x) | 0.00 (4.7x) | True | | 140000 | 0.32 | 0.02 (14.7x) | 0.02 (1.1x) | 0.00 (4.1x) | True | | 160000 | 0.40 | 0.03 (13.1x) | 0.03 (1.2x) | 0.01 (4.6x) | True | | 180000 | 0.51 | 0.03 (14.7x) | 0.03 (1.1x) | 0.01 (4.4x) | True | | 200000 | 0.62 | 0.04 (16.6x) | 0.03 (1.1x) | 0.01 (4.4x) | True | | 220000 | 0.75 | 0.05 (16.1x) | 0.04 (1.1x) | 0.01 (4.9x) | True | | 240000 | 0.89 | 0.05 (17.1x) | 0.05 (1.0x) | 0.01 (4.7x) | True | | 260000 | 1.04 | 0.06 (18.1x) | 0.06 (1.0x) | 0.01 (4.5x) | True | | 280000 | 1.20 | 0.06 (20.2x) | 0.06 (1.0x) | 0.01 (4.2x) | True | | 300000 | 1.38 | 0.07 (19.4x) | 0.07 (1.1x) | 0.02 (4.4x) | True | +--------+----------+--------------+--------------+--------------+-------+
実際には、よく知られている繰り返し式の代わりに数字のシーケンスを使用すると、より複雑な状況に直面する可能性があります。
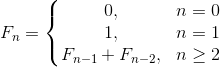
これは、たとえば次のようなやや複雑な式で与えられます。

この場合、インターネット上で上記のアルゴリズムの実装を見つけることはできませんが、行列を累乗するアルゴリズムを手動で見つけるにはかなりの時間がかかります。 それにもかかわらず、ソリューションを「額」として記述し、デコレータを適用することができます。そうすれば、コンピューターは簡単なアルゴリズムを思い付きます。
from cpmoptimize import cpmoptimize @cpmoptimize() def f(n): prev3 = 0 prev2 = 1 prev1 = 1 for i in xrange(3, n + 3): cur = 7 * (2 * prev1 + 3 * prev2) + 4 * prev3 + 5 * i + 6 prev3, prev2, prev1 = prev2, prev1, cur return prev3
例3 等比数列の合計
等比数列のcountメンバーの合計を計算する必要があるとします。最初のメンバーstartと分母coeffが与えられます。 このタスクでは、デコレータは簡単なソリューションを最適化できます。
from cpmoptimize import cpmoptimize @cpmoptimize() def geom_sum(start, coeff, count): res = 0 elem = start for i in xrange(count): res += elem elem *= coeff return res
グラフ 

例番号4。 べき乗
数aを非負の整数nに累乗する必要があるとします。 このようなタスクでは、デコレータは実際に簡単な解決策をバイナリべき乗アルゴリズムに置き換えます。
from cpmoptimize import cpmoptimize @cpmoptimize() def power(a, n): res = 1 for i in xrange(n): res *= a return res
グラフ 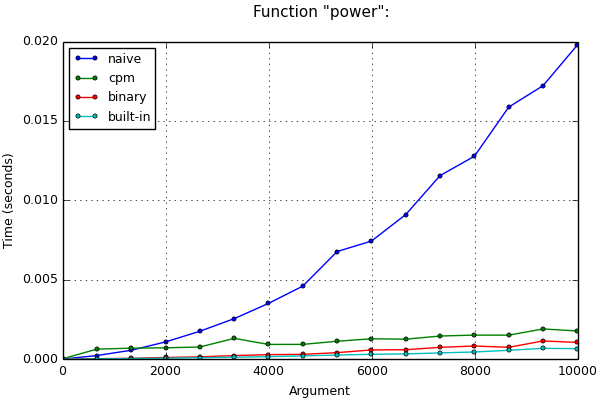

ダウンロードリンク
pipを使用してライブラリをインストールできます。
sudo pip install cpmoptimize
サンプル付きのライブラリのソースコードは、無料のMITライセンスの下でgithubで入手できます。
UPD。 パッケージはPython Package Indexで公開されています。
最適化の例は、「 tests / 」フォルダーにあります。 各例は、「直接的な」ソリューション、最適化されたバージョンを表す関数、および特定の問題に対するよく知られた複雑だが迅速なソリューションを表す関数で構成されています。 これらの関数は、さまざまなテストグループで実行するスクリプトに配置され、作業時間を測定し、対応するテーブルを構築します。 matplotlibライブラリがインストールされている場合、スクリプトは入力データ(通常または対数)に対する関数のランタイムの依存関係のグラフも作成し、それらを " tests / plots / "フォルダーに保存します。
ライブラリの説明
ライブラリを作成する際、Pythonインタープリターが作成するプログラムのバイトコードを解析し、インタープリターに干渉することなく実行時に変更できるという事実を利用しました。これにより、言語を拡張する可能性が広がります(たとえば、 gotoコンストラクトの実装を参照)。 通常、Pythonに組み込まれている長い演算を使用すると、説明した方法の利点が現れます。
これらの理由から、説明した最適化をPythonで実装することは、私にとってより興味深いタスクになりましたが、もちろん、C ++コンパイラで使用すると、さらに高速なプログラムを作成できます。 さらに、デコレータに最適化されたPythonコードは、漸近的な動作が優れているため、C ++コードの額を追い越す傾向があります。
バイトコードを変更するとき、 byteplayモジュールを使用しました。 このモジュールは、バイトコードを分解および組み立てるための便利なインターフェイスを提供します。 残念ながら、このモジュールはまだPython 3に移植されていないため、プロジェクト全体をPython 2.7で実装しました。
cpmoptimizeライブラリの名前は、 「マトリックスの電力を計算して最適化する 」の略です。 この記事のボリュームでは、バイトコードの分析と変更のプロセスを詳細に説明することはできませんが、このライブラリが提供する機能とその作業の基礎となる原則について詳細に説明しようとします。
自分のxrange
cpmoptimize。 xrange ( 停止 )
cpmoptimize。 xrange ( start 、 stop [、 step ])
最適化のためのPython 2の組み込みxrange型は、引数としてlong型のlong整数をサポートしていません。
>>> xrange(10 ** 1000) Traceback (most recent call last): File "<stdin>", line 1, in <module> OverflowError: Python int too large to convert to C long
ライブラリを使用する場合、順序の操作の数で循環するため
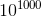 1秒未満で実行でき、プログラムで一般的になります。ライブラリは、純粋なPythonでxrange型の独自の実装を提供します(ライブラリ内ではCPMRangeと呼ばれます )。 通常のxrangeのすべての機能と、さらにlong型の引数をサポートします。 このようなコードはエラーにならず、正しい結果をすばやく計算します。
1秒未満で実行でき、プログラムで一般的になります。ライブラリは、純粋なPythonでxrange型の独自の実装を提供します(ライブラリ内ではCPMRangeと呼ばれます )。 通常のxrangeのすべての機能と、さらにlong型の引数をサポートします。 このようなコードはエラーにならず、正しい結果をすばやく計算します。
from cpmoptimize import cpmoptimize, xrange @cpmoptimize() def f(): res = 0 for i in xrange(10 ** 1000): res += 3 return res print f()
それでも、あなたの場合、サイクルの反復回数が少ない場合、デコレータで組み込みのxrangeを使い続けることができます。
Cpmoptimize関数
cpmoptimize。 cpmoptimize ( strict = False、 iters_limit = 5000、 types =(int、long)、 opt_min_rows = True、 opt_clear_stack = True)
デコレータアプリケーション
cpmoptimize関数は、実行された最適化のパラメーターを受け入れ、これらのパラメーターを考慮したデコレーターを返します。デコレーターは、最適化された関数に適用する必要があります。 これは、特別な構文(「犬」記号の有無にかかわらず)を使用して実行できます。
from cpmoptimize import cpmoptimize @cpmoptimize() def f(n): # def naive_g(n): # smart_g = cpmoptimize()(naive_g)
バイトコードを変更する前に、元の関数がコピーされます。 したがって、上記のコードでは、関数fとsmart_gは最終的に最適化されますが、 naive_gは最適化されません。
ループを検索する
デコレータは、関数のバイトコードで標準のループを探しますが、 whileループとジェネレーターおよびリスト式内のforループは無視されます。 ネストされたループはまだサポートされていません(最も内側のループのみが最適化されています)。 その他の構造は正しく処理されます。
許可されたタイプ
デコレータは、ループで使用される変数のタイプに関係なく、ループを最適化できません。 実際、たとえばPythonでは、乗算ごとに文字列をファイルに書き込むタイプを決定できます。 最適化を適用した結果、関数で行われた乗算の数が変わる可能性があります。 このため、ファイルの行数が異なり、最適化によりプログラムが中断されます。
さらに、行列を使用した操作では、変数が暗黙的に追加および乗算されるため、変数のタイプを「混在させる」ことができます。 定数または変数のいずれかがfloat型の場合、コードの実行後にint型になっているはずの変数もfloat型になる可能性があります( intとfloatを追加するとfloatが返されるため )。 このような動作は、プログラムでエラーを引き起こす可能性があり、受け入れられません。
不要な副作用を避けるため、デコレータは、ループで使用されるすべての定数と変数が有効なタイプである場合にのみループを最適化します。 初期の有効な型はintおよびlong 、およびそれらから継承された型です。 定数または変数のいずれかがlong型の場合、コードの実行後にint型になっているはずの変数もlong型にすることができます。 ただし、Pythonのintとlongは十分に互換性があるため、エラーにつながることはありません。
有効なタイプのセットを変更する場合(たとえば、 floatのサポートを追加する場合)、 typesパラメーターで必要なタイプのタプルを渡す必要があります。 このタプルの一部であるか、このタプルの一部である型から継承された型は有効と見なされます。 実際、 値に有効な型があるかどうかの確認は、式isinstance(value、types)を使用して実行されます。
サイクル最適化条件
見つかった各サイクルは、多くの条件を満たす必要があります。 それらのいくつかは、デコレータを使用するときにすでにチェックされています。
- ループの本体は、代入命令、単項および二項演算のみで構成され、それらを組み合わせて複雑な式にすることができます。 条件、他の関数の呼び出し、 returnおよびyieldステートメントなどを含めることはできません。
- オペランドには、 予測可能性の条件が必要な場合があります。サイクルの各反復で、それらの値は同じでなければならず、前の反復での計算の結果に依存してはなりません。 この場合:
- 単項マイナスのオペランドと同様に、加算および減算のすべてのオペランドは、予測不能である可能性があります。
- 乗算の少なくとも1つのオペランドは予測可能でなければなりません(元のインタープリターでは定数による乗算のみがサポートされていたという事実に似ています)。
- べき乗、除算、剰余演算、およびビット単位演算のすべてのオペランドは予測可能でなければなりません。
- ループで使用されるすべての定数は、有効なタイプである必要があります。
これらの条件が満たされると、サイクルの前に「トラップ」が設定され、条件の別の部分がチェックされますが、サイクルの元のバイトコードは削除されません。 Pythonは動的型付けを使用するため、次の条件はループを開始する直前にのみチェックできます。
- ループが通過するオブジェクトには、このcpmoptimize.xrangeライブラリの標準xrange型またはその類似体が必要です。 ただし、リストを返す低速範囲関数はサポートされていません。
- ループで使用されるすべての変数の値は有効なタイプです。
「トラップ」が最適化が許容可能であると結論付けた場合、必要なマトリックスが計算され、使用される変数の値が新しいものに変更されます。 最適化を実行できない場合、ループの元のバイトコードが起動されます。
サイクルごとの式とコードの削除
説明されている方法はべき乗とビット単位のAND演算をサポートしていないという事実にもかかわらず、次のコードが最適化されます。
@cpmoptimize() def f(n, k): res = 0 for i in xrange(n): m = 3 res += ((k ** m) & 676) + i return res
バイトコードを分析するとき、デコレータは、式(k ** m)および676の変数kおよびmの値は、それらが使用されるサイクルの反復に依存せず、したがって式全体の値は変化しないと結論付けます。 各反復で計算する必要はありません;この値を一度計算すれば十分です。 したがって、対応するバイトコード命令を取り出して、サイクルの開始直前に実行し、サイクル内の既製の値を置き換えることができます。 コードは次のように変換されます。
@cpmoptimize() def f(n, k): res = 0 m = 3 _const1 = (k ** m) & 676 for i in xrange(n): res += _const1 + i return res
( loop-invariant code motion ). , , ( _const1 k ). .
. , « » , .
デコレータは、複数の割り当ても部分的にサポートします。要素がほとんどない場合、Pythonはタプルを使用せずにデコレータでサポートされているバイトコードを作成します。
a, b = b, a + b
しきい値iters_limit
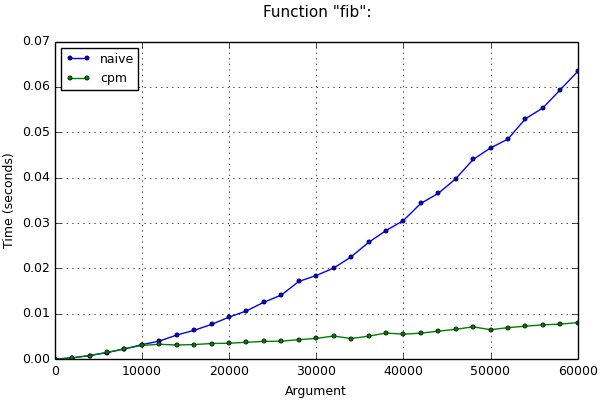
上記のグラフでは、反復回数が少ない場合、最適化されたサイクルの動作が通常よりも遅くなることがあります。この場合、行列と型チェックの構築にまだ時間がかかるためです。関数が可能な限り高速で、少数の反復で動作する必要がある場合、iters_limitパラメーターを使用して明示的にしきい値を設定できます。次に、最適化を開始する前の「トラップ」は、ループが完了しなければならない反復回数をチェックし、この数が指定されたしきい値を超えない場合、最適化をキャンセルします。
最初に、しきい値は5000回の反復に設定されます。 2回の反復より低く設定することはできません。
最も好ましいしきい値は、関数の最適化されたバージョンと初期バージョンの動作時間に対応する線グラフ上の交点です。しきい値がこのように正確に設定されている場合、この場合、関数は最速のアルゴリズムを選択できます(最適化または初期)。
厳格なフラグ
場合によっては、最適化が必須です。そのため、
 最適化せずに反復のループ内にある場合、プログラムは単にフリーズします。この場合、strictパラメーターが提供されます。最初は、その値はFalseですが、Trueに設定されている場合、標準forループの1つが最適化されていないと、例外がスローされます。
最適化せずに反復のループ内にある場合、プログラムは単にフリーズします。この場合、strictパラメーターが提供されます。最初は、その値はFalseですが、Trueに設定されている場合、標準forループの1つが最適化されていないと、例外がスローされます。
デコレータを適用する段階で最適化が適用できないという事実が検出された場合、例外cpmoptimize.recompiler.RecompilationErrorがすぐに発生します。ループの例では、2つの予測不能な変数が乗算されます。
>>> from cpmoptimize import cpmoptimize >>> >>> @cpmoptimize(strict=True) ... def f(n, k): ... res = 0 ... for i in xrange(n): ... res += i * res ... return res ... Traceback (most recent call last): File "<stdin>", line 1, in <module> File "cpmoptimize/__init__.py", line 100, in upgrade_func index += analyze_loop(settings, code, index) + 1 File "cpmoptimize/__init__.py", line 59, in analyze_loop raise err cpmoptimize.recompiler.RecompileError: Multiplication of two unpredictable values is unsupported
ループの実行前にその最適化が適用できないことが検出された場合(つまり、反復子の値または変数のタイプがサポートされていないことが判明した場合)、TypeError例外がスローされます。
>>> from cpmoptimize import cpmoptimize >>> >>> @cpmoptimize(strict=True) ... def f(iterable): ... res = 0 ... for elem in iterable: ... res += elem ... return res ... >>> f(xrange(30)) 435 >>> f(range(30)) Traceback (most recent call last): File "<stdin>", line 1, in <module> File "<stdin>", line 4, in f File "cpmoptimize/hook.py", line 170, in exec_loop raise err TypeError: Iterator in optimized loops must have type "xrange" instead of <type 'list'>
追加の最適化オプション
opt_min_rowsとopt_clear_stackの 2つのフラグは、マトリックスを構築するときに追加の最適化メソッドを使用する役割を果たします。最初はオンになっており、オフにする機能はデモ目的でのみ存在します(おかげで、これらの方法の有効性を比較できます)。
最適化されたコードを実行すると、生成されたマトリックスの一部のセルで長い時間の乗算が時間の大半を占めます。この時間のかかるプロセスと比較すると、他のすべてのセルの増殖に費やされる時間はごくわずかです。
式を再コンパイルするプロセスで、デコレータは中間の仮想インタプリタスタックの位置を担当する変数。複雑な計算の後、他の実際の変数にすでに格納されている長い数値が残る場合があります。これらの値をもう一度保存する必要はありませんが、マトリックスのセルに残ってプログラムを大幅に遅くします。マトリックスを乗算すると、これらの長い数値を再度乗算する必要があるためです。opt_clear_stackオプションは、そのような変数をクリアする責任があります。使用の最後にそれらをゼロに割り当てると、それらの長い値は消えます。
このオプションは、プログラムが非常に大きな数で動作する場合に特に効果的です。このような数値の不必要な乗算を排除することにより、プログラムを2倍以上高速化できます。Opt_min_rows
オプション乗算する正方行列のサイズを最小化する必要があります。未使用および予測可能な変数に対応する行は、行列から除外されます。ループ変数自体が使用されない場合、正しい値を維持する責任がある行も除外されます。プログラムを中断させないために、サイクル後、これらの変数にはすべて正しい最終値が割り当てられます。さらに、元の記事では、変数のベクトルに単一性に等しい要素が追加されました。この要素に対応する行が使用されていない場合、それも除外されます。
このオプションは、数値がまだそれほど長くなっておらず、マトリックスの次元がプログラムの実行時間に大きく貢献している場合、nがそれほど大きくない場合にプログラムをわずかに高速化できます。
両方のオプションを同時に使用すると、仮想変数は予測可能な(ゼロ)値を持ち始め、opt_min_rowsはさらに効率的に機能します。言い換えると、両方のオプションの有効性は、それぞれのオプションの有効性よりも優れています。
以下のグラフは、特定のオプションを無効にした場合のフィボナッチ数を計算するためのプログラムの動作時間を示しています(「-m」はopt_min_rowsが無効なプログラム、「-c」はopt_clear_stackが無効なプログラム、「-mc」は両方のオプションがすぐに無効なプログラムです) ):

他に何を実装できますか?
一連の操作を変更する
以下の場合、 このメソッドはいくつかの操作をサポートすると言います
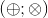 。
。
 2つの変数、または変数と定数に対して操作を実行できます。
2つの変数、または変数と定数に対して操作を実行できます。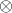 変数と定数に対して操作を実行できます。
変数と定数に対して操作を実行できます。
メソッドがいくつかの操作をサポートしていることは既に知っています。
 。 確かに:
。 確かに:
- 2つの変数または変数と定数を追加できます。
- 変数に定数を掛けることができます。
現在、最適化デコレータに実装されているのはこれらの操作です。ただし、説明されている方法は、
 (乗算とべき乗のペア)などの他の操作のペアをサポートしていることがわかります。
(乗算とべき乗のペア)などの他の操作のペアをサポートしていることがわかります。
たとえば、繰り返し関係で指定されたシーケンスのn番目の番号を見つけることがタスクの
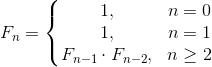
場合です。デコレーターがいくつかの操作をサポートしている場合
 、変数に別の変数を掛けることができます(ただし、変数を追加することはできません)。この場合、この問題に対する次の簡単な解決策は、デコレータによって加速できます。
、変数に別の変数を掛けることができます(ただし、変数を追加することはできません)。この場合、この問題に対する次の簡単な解決策は、デコレータによって加速できます。
def f(n): a = 1 b = 1 for i in xrange(n): a, b = b, a * b return a
メソッドが操作のペアもサポートしていることを証明できます
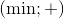 、
、  そして
そして 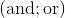 (ここで、ビット単位のAND またはビット単位のORです)。正の数の場合、操作のペアで作業できます
(ここで、ビット単位のAND またはビット単位のORです)。正の数の場合、操作のペアで作業できます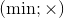 そして
そして 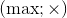 。
。
 たとえば、操作のサポートを実装するには、変数の値ではなく、これらの値の対数で操作することができます。次に、変数の乗算は対数の加算に置き換えられ、変数の定数の累乗は、対数に定数を乗算することにより行われます。したがって、我々は問題を操作で既に実現されたケースに減らします
たとえば、操作のサポートを実装するには、変数の値ではなく、これらの値の対数で操作することができます。次に、変数の乗算は対数の加算に置き換えられ、変数の定数の累乗は、対数に定数を乗算することにより行われます。したがって、我々は問題を操作で既に実現されたケースに減らします 。
。
指定された残りの操作ペアのサポートを実装する方法の説明には、一定の数の数学計算が含まれており、別の記事に値します。現時点では、操作のペアはある程度互換性があることに言及するだけです。
入れ子ループ
バイトコードでループ分析アルゴリズムを改良することにより、ネストされたループのサポートを実装して、次のようなコードを最適化できます。
def f(): res = 0 for i in xrange(10 ** 50): for j in xrange(10 ** 100): res += i * 2 + j return res
予測可能な条件
次のコードでは、ループ本体の条件は予測可能です。サイクルを開始する前に、それが正しいかどうかを確認し、実行されていないコードブランチを削除できます。結果のコードは最適化できます:
def f(mode): res = 0 for i in xrange(10 ** 50): if mode == 1: res += 3 else: res += 5 return res
結論
一般的に、Pythonインタープリターは、作成したソースコードとほぼ正確に一致する予測可能なバイトコードを生成します。デフォルトでは、関数のインライン展開、ループの展開、プログラムの動作の分析を必要とするその他の最適化は実行されません。バージョン2.6以降のみ、CPythonは定数演算式を折りたたむことを学びましたが、この機能は常に効率的に機能するとは限りません。
この状況にはいくつかの理由があります。第一に、Pythonの一般的な場合のコードの分析は困難です。これは、データ型はプログラムの実行中にしか追跡できないためです(この場合はこれを行います)。第二に、原則として、最適化ではまだPythonが純粋にコンパイルされた言語の速度を達成できないため、プログラムを非常に迅速に動作させる必要がある場合は、単純に低レベル言語で記述することをお勧めします。
ただし、Pythonは柔軟な言語であるため、必要に応じてインタープリターに干渉することなく、多くの最適化メソッドを自分で実装できます。このライブラリと、以下にリストされている他のプロジェクトは、この機会をよく示しています。
UPD。プロジェクトの説明は、SlideShareのプレゼンテーションとしても利用できます。
こちらもご覧ください
以下に、Pythonでプログラムの実行を高速化するためのいくつかの他の興味深いプロジェクトへのリンクを示します。
- PyPyは、JITコンパイルをサポートする代替のPythonインタープリターです。これにより、原則として、Pythonプログラムをより高速に実行できます。PyPy自体はRPythonで記述されており、Cコードへのトランスレーターは特別に設計されています。
- Pystonは、コードをLLVMツールを使用して最適化し、JITコンパイルを使用して実行できる中間LLVM表現に変換する、新しい代替Pythonインタープリターです。
- Nuitka — Python. py2exe, *.exe-, , , Nuitka Python .
- WPython — CPython 2.6.4 -, .
- astoptimizer — , - .
- promise — , -, «». , , .
- foldy.py — , - ( constant folding ), , .
- , - ( constant binding ), .
UPD#1。ユーザーマジックは、いくつかのリンクを示唆しました。
- NumPyは(Cで記述されたPythonモジュールを備えた)ライブラリであり、大規模な配列と行列を使用した計算を迅速に実行できるだけでなく、高度な数学関数の広範なセットを使用できます。
- Numbaは、配列を使用した数学的計算と演算を含むプログラムを高速化するライブラリです。最適化は、コードをネイティブCPUおよびGPU命令に変換するJITコンパイル(LLVMを使用する場合)、およびその他の古典的な方法によるものです。
- Numexprは、対応するバイトコードの分析と変更を通じて数式の計算を高速化するライブラリです。式はいくつかの部分に分割できます。その一部は、他の部分よりも頻繁に再計算されず、コードの並列化などによって加速されます。
- CythonはPython言語のスーパーセットの最適化コンパイラであり、プログラムで静的型付けを使用し、CおよびC ++コードと密接にやり取りすることができます。
- JITコンパイルによりPythonでのさまざまな計算を高速化するライブラリの概要を含む記事。
UPD#2。DuneRatユーザーは、他のいくつかのPythonコンパイルプロジェクトを示しました:shedskin、hope、pythran。