この記事では、音楽を検索した方法を説明します。
さあ、行こう!
私の前の仕事は次のとおりです。音楽作品のパッセージがあり、音楽作品のベースがあり、このパッセージが利用可能な音楽作品のどれであるかを見つける必要があります。
誰が気にし、harbokatの下で読んでください。
これらの目的のために、周波数対時間の関数として音楽を提示することにしました。
これを行うには、次のことを行います。
図に示すように、信号をウィンドウに「スライス」し、スライディングウィンドウアルゴリズムの修正を使用します。 変更は、ウィンドウが信号上で「スムーズに滑る」のではなく、「突然移動する」、つまりウィンドウがオーバーラップするという事実から成ります。

ウィンドウとして、いわゆる「ハミングウィンドウ」を使用します。
1つまたは別の周波数を持つコンポーネントの外観の瞬間として、ウィンドウの中央に対応する瞬間を取ります。 この変更により、時間領域と周波数領域の解像度が向上します。比較的大きなウィンドウによる周波数領域、およびハミングウィンドウのメインローブが比較的狭いという事実による時間領域で、重複してウィンドウを移動すると、時間サンプルを非常に正確に記録できます。
各ウィンドウで、このウィンドウに存在する一連の周波数を取得するために、フーリエ変換を実行します。
任意の構成の合計は、次を取得します。
入力時-振幅の時間依存性:
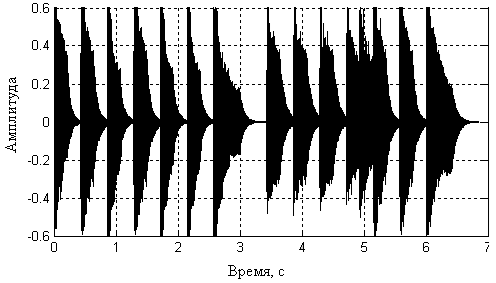
そして出力-周波数の振幅の依存性:
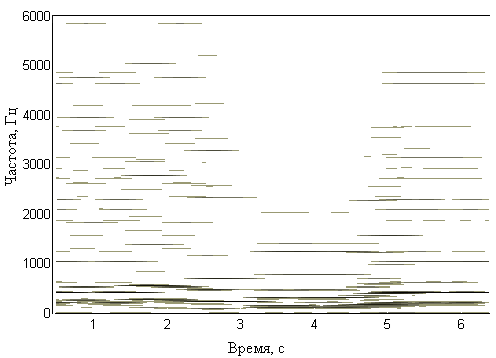
これで終わりではありません。
時間周波数表現を取得した後、さまざまな干渉を除去し、音符に対応する周波数を選択します。
したがって、時間と音の表現、つまり時間と音の数の関数を取得します。
しかし、ここでは、たとえば、異なるメロディーから同じメロディーを演奏できるという事実に直面しています(図(a)では高いノート、図(b)では低いノート):
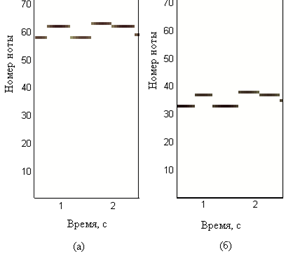
しかし、写真を見ると、写真が似ていることがわかります。
ここから次のアイデアが生まれました:音楽作品を識別するために、演奏された調性に関係なく、音符の数と出現時間の絶対値ではなく、相対的なもの-次と前の音符と時間のサンプルの値の違いを考慮する必要があります。
そのため、時間ノート関数から2行のマトリックスを取得できます。1行にはノートの違いがあり、もう1行には外観の時間の違いがあるため、リズムを考慮します。
作品が異なるキーで演奏されたという事実にもかかわらず、次の比率は真実です:
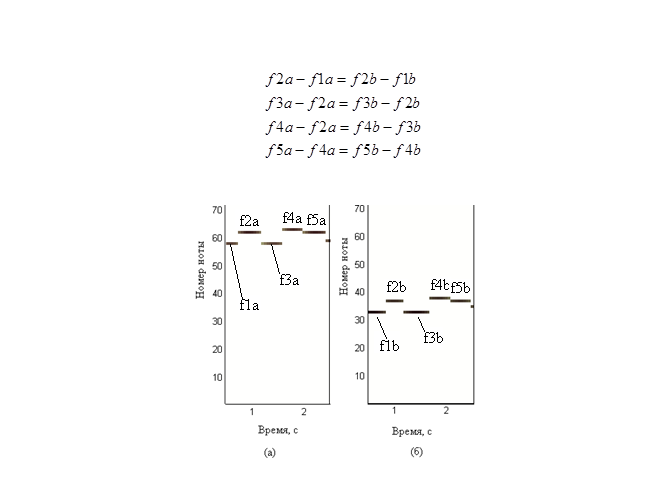
識別アルゴリズムは次のとおりです。
- 信頼区間のベクトルが計算されます-サンプルに対して受け入れられた信号のオーディオインプリントが取得され(この場合、2行と特定の列数の行列です)、同じサイズのベクトルが計算され、その要素はサンプル内の対応する要素の絶対値の30%に等しくなります;
- スライディングウィンドウの原理に従って、小さなオーディオプリントが大きなオーディオプリントに沿って移動します。 この場合、対応する要素の差のモジュールが考慮され、この差が信頼区間のベクトルの対応する要素以下になるように検証が行われます。
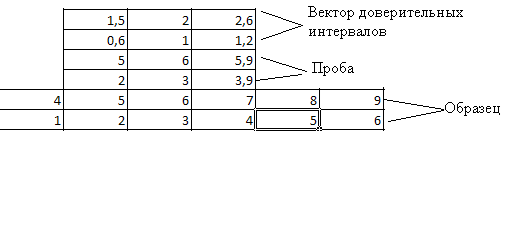
- この差が大きくない場合、列の数が考慮されます。 条件を満たす;
- この数値は、「より小さい」オーディオプリントの列数で正規化されます。
- その後、類似度の最大シェアが選択されます。
さらに、私の場合の類似点のシェアが75%を超えている場合、メロディが見つかったと思います。