
理論のビット
私たちの雰囲気は完全に透明ではありません:空気に加えて、産業企業や車の排気ガスのために、都市では原則としてさまざまな方法でそこに到達するガスと塵があります。 このすべてにより、大気を通過する放射は大幅に減衰します。 そして、光が大気中を移動する経路が長いほど、この減衰は強くなります。 下の図を見ると、大気中のパスが長いほど、光源の高さが低いことがわかります。

大気中の光ビームの長い経路の光源の高さへの依存性を推測してみましょう。

この三角形に正弦定理を適用します。
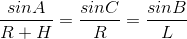
A = 90 + h(hは星の高さ)という事実を使用すると、次のようになります。
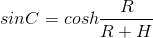
さらに、サイン定理の最初と最後の関係、および三角形の角度の合計に関する定理を使用して、次のように取得します。
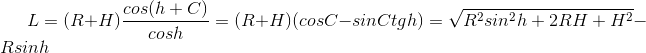
ここでは、次の事実を使用しました。
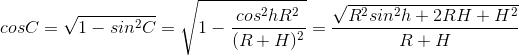
ただし、大気中の経路長は通常、長さの次元ではなく無次元の表現で表されます。つまり、大気中の光線の経路長は均質な大気の高さで表され、そのような単位は大気質量(eng:airmass)と呼ばれます。 地球の半径と均一な大気の高さの比をk = R / Hとする(k = 800)
気団では、式は次の形式を取ります。
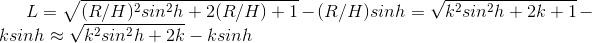
次に、通過した気団に応じて、大気中で光がどのように減衰するかを理解する必要があります。 これを説明する法律は、 ブーガーの法則と呼ばれます。
恒星規模では、法則はかなり単純な形式を取ります。
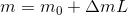
どこで:
mは観測された大きさです
m0-大気圏外の星の輝き
Δm-天頂での大気吸収
L-気団
測光に関する少しの理論
次に、測光について少し説明します。 写真で星の明るさを測定するとき、その大きさmは機器の大きさMに対して相対的に与えられます。
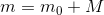
ここで、m0は実際の大きさです。
次に、機器の大きさMは次のようになります。
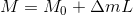
ここで、M0は大気圏外の機器の大きさです。
これが私たちの吸収が隠れるところです。
したがって、私たちの主なタスクは、天頂Δmでの吸収を見つけることでした
練習する
今すぐ練習しましょう まず、測光用のソフトウェアが必要です。 そして、それはすべての天体写真家の働き者になるでしょう-IRIS
最初に行うことは、rawデコードです。
まず、ファイル->設定で作業ディレクトリを設定します
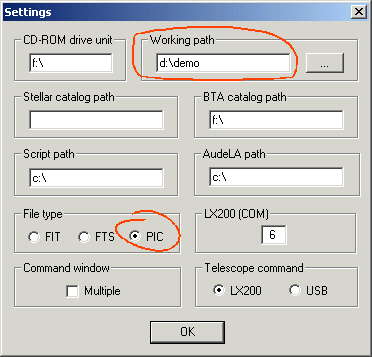
次に、カメラの設定でカメラのパラメーターを設定します。
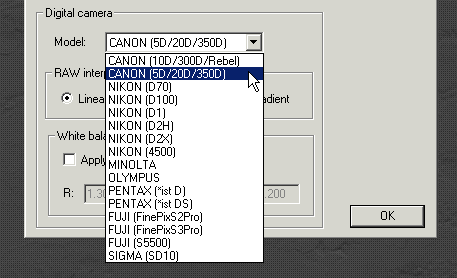
最後にRAWをデコードします:デジタル写真-> RAWファイルをデコードします。
デコード後、[完了]ボタンを押すと、画像が画面に表示されます。 これで測光の準備が整いました。
[分析]-> [開口測光]を選択する必要があります。 ドロップダウンウィンドウに単純に同意して作業を開始することをお勧めします。 カーソルの代わりに3つの円が表示され、タスクはそのようなカーソルの中心を星に移動してクリックすることです。 クリックすると、次のデータが出力ウィンドウに表示されます。
撮影モード3-(979、2553)
内側の円のピクセル数= 197
背景評価のピクセル数= 816
強度= 52348.0-大きさ= -11.797
バックグラウンド平均レベル= 2755.0
最後の2行に興味があります。
強度= 52348.0-任意単位の強度
大きさ= -11.797-機器の大きさの光沢(0の場合、この輝度は1ピクセルの強度が1である場合に取得されます)
バックグラウンド平均レベル= 2755.0-任意単位のバックグラウンド電流。
次に、Stellariumを開いて星を特定する必要があります。 この情報は、MS Excelなどのテーブルに入力する必要があります。
私は次のようにしました:

このようなテーブルには、星に関する可能な限り多くの情報を入力する必要があります。 必然的に彼女のカタログの光沢(Cat mag)、測定された光沢(Mag Image)および高さは、Stellarium(Alt)によって決定されました。 混乱しないように、カタログの星番号(星の名前)を書き留めておくことをお勧めします。強度値と背景値を書き留めておくこともお勧めします。
次に、大気の質量(気団)が各星の高さによって計算されます。 次に、差として機器の大きさDmを見つけます。Dm= Mag image-Cat mag
注意してください! 異なる高さの星、特に低い星については、できるだけ多くのデータを入力する必要があります。 結局のところ、データが多いほど、最終結果はより正確になります。 さらに、キャリブレーションフレームを作成しなかったため、測光の効果はノイズによってさまざまな程度に影響を受けます。 一方、星は色が異なり、その結果、放射の最大値は異なる周波数にあり、異なる周波数では吸収が大幅に異なる可能性があります...
私の詳細
| 日付 | 06/19/14 23:53 | ID画像 | 252 | ||||
| 星の名前 | 猫マグ | Alt | マグ画像 | 強度 | BI | Dm | エアマス |
| 20ブー | 4.8 | 41.07 | -11,128 | 28253 | 2468 | -15,928 | 1,520865865 |
| f boo | 5,4 | 44.38 | -10.35 | 13798 | 2457 | -15.75 | 1,428837794 |
| 14ブー | 5.5 | 37.5 | -10,545 | 16518 | 2482 | -16,045 | 1,64094179 |
| 15ブー | 5.25 | 35.1 | -10.525 | 16225 | 2483 | -15,775 | 1,736922288 |
| HIP 70400 | 5.1 | 32,4 | -10.645 | 18118 | 2463 | -15,745 | 1.863391058 |
| ブー | 4.05 | 36,073 | -12.06 | 66655 | 2516 | -16.11 | 1,696331832 |
| 70 vir | 4.95 | 32,2 | -11,021 | 25616 | 2565 | -15,971 | 1,873663569 |
| 71 vir | 5.65 | 29.85 | -10,324 | 13476 | 2556 | -15,974 | 2,005323345 |
| e vir | 5.15 | 27 | -10,352 | 13833 | 2589 | -15,502 | 2.197418439 |
| eps vir | 2.85 | 26.22 | -12,864 | 139837 | 2607 | -15,714 | 2.25757501 |
| HIP 63420 | 6.7 | 24.72 | -8,949 | 3799 | 2614 | -15,649 | 2,384289105 |
| シグマvir | 4.75 | 23.08 | -11,065 | 26671 | 2585 | -15,815 | 2,542206706 |
| 84 vir | 5,4 | 25.5 | -10,561 | 16761 | 2533 | -15,961 | 2,316481972 |
| d2 vir | 5.2 | 21.18 | -10.612 | 17567 | 2631 | -15,812 | 2,756376852 |
| d1 vir | 5.55 | 19.95 | -9,792 | 8067 | 2639 | -15,342 | 2.917077172 |
| c vir | 4.95 | 14 | -10.826 | 21403 | 2656 | -15,776 | 4.092871581 |
| pi vir | 4.65 | 13.82 | -10,764 | 20209 | 2676 | -15,414 | 4,144019169 |
| o vir | 4.1 | 16.17 | -11.44 | 37660 | 2658 | -15.54 | 3,564544399 |
| 6 com | 5.05 | 22.67 | -10.65 | 18196 | 2625 | -15.7 | 2,58533522 |
| 12 vir | 5.85 | 18.06 | -9,255 | 4729 | 2647 | -15.105 | 3,20695548 |
| 11 com | 4.7 | 25.65 | -11,084 | 27144 | 2610 | -15,784 | 2,303928428 |
| 24 Com A | 4.95 | 28.23 | -11,226 | 30929 | 2614 | -16,176 | 2,109551775 |
| 23 com | 4.95 | 22.55 | -11,069 | 26766 | 2596 | -16.019 | 2.598260423 |
| 31 com | 4.9 | 37.07 | -10,961 | 24233 | 2546 | -15,861 | 1,657141284 |
| ベータ版 | 4.2 | 40.93 | -11,658 | 46037 | 2523 | -15,858 | 1,525134451 |
| 37 com | 5.05 | 41.35 | -11,107 | 27728 | 2521 | -16,157 | 1,51242676 |
| HIP 62972 | 6.25 | 42.04 | -9.77 | 8091 | 2500 | -16.02 | 1.492174262 |
| 14 CVn | 5.2 | 45.68 | -10,579 | 17050 | 2481 | -15,779 | 1.396892826 |
| HIP 62641 | 5.85 | 44.53 | -10.011 | 10102 | 2476 | -15,861 | 1.425039994 |
| HIP 64543 | 6.65 | 44.6 | -9,463 | 6099 | 2496 | -16,113 | 1.423277903 |
| HIP 63267 | 7.15 | 24.18 | -8,605 | 2767 | 2613 | -15,755 | 2,43386583 |
| HIP 63221 A | 7.5 | 23,23 | -8,819 | 3371 | 2604 | -16,319 | 2,526815663 |
| デルタvir | 3.35 | 18.95 | -12,289 | 82359 | 2620 | -15,639 | 3.063224414 |
| 37 vir | 6 | 18.12 | -9,783 | 8185 | 2620 | -15,783 | 3.19682149 |
| 33 vir | 6.4 | 18,017 | -9,468 | 6129 | 2625 | -15,868 | 3,214259678 |
| HIP 61658 | 5.65 | 15.27 | -9,789 | 8237 | 2643 | -15,439 | 3,765690356 |
| HIP 61637 | 6.3 | 16,4 | -8,518 | 2554 | 2647 | -14.818 | 3,516648775 |
| HIP 60850 | 6.7 | 15.92 | -9.29 | 5201 | 2658 | -15.99 | 3,618160686 |
| エタvir | 3.85 | 10.57 | -11,084 | 27151 | 2690 | -14,934 | 5.357099392 |
| 10 vir | 5.95 | 11.18 | -7,493 | 994 | 2702 | -13,443 | 5,077628047 |
| b vir | 5.35 | 11.18 | -8,788 | 3275 | 2706 | -14,138 | 5,077628047 |
| HIP 58809 | 6.35 | 13.28 | -8,545 | 2618 | 2684 | -14.895 | 4.305596468 |
| 11 vir | 5.7 | 14.42 | -8,837 | 3425 | 2677 | -14,537 | 3.97839932 |
| 17 vir | 6.45 | 15.81 | -9,352 | 5507 | 2657 | -15,802 | 3,642283826 |
次に、機器の大きさ(Dm)の気団(Airmass)への依存関係のグラフを作成する必要があります。 散布図のタイプを選択します。 次に、最小二乗法を使用して、このグラフに最適な線形方程式を見つける必要があります。 これを行うには、上のメニューに移動します。チャートの操作->レイアウト->トレンドライン->トレンドラインの追加パラメーター。 ここで、線形タイプを選択し、「ダイアグラムに方程式を表示」項目にチェックを入れます
私はこのグラフのようなものを得ました:
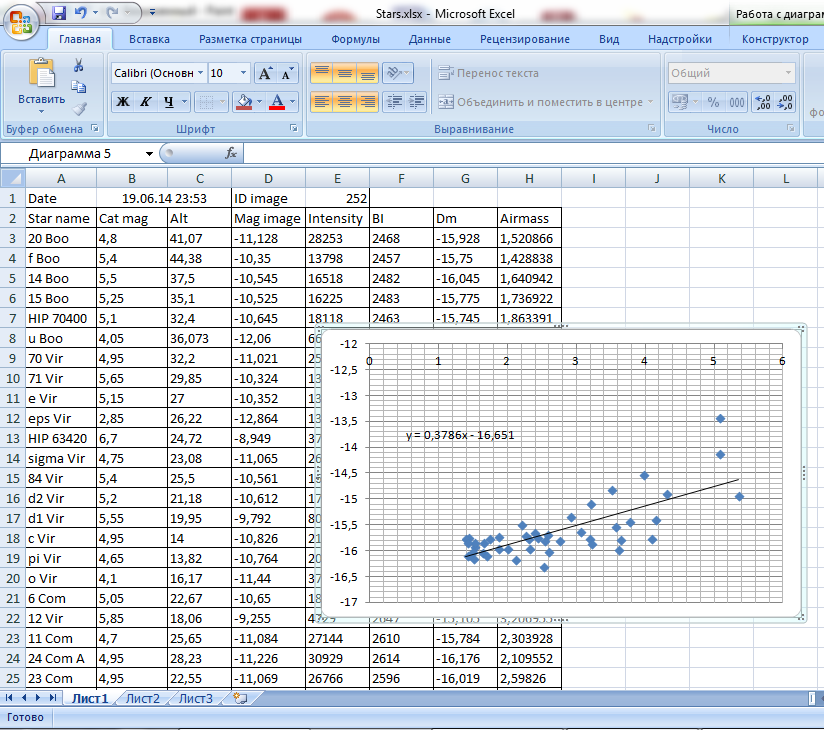
方程式を見ると、0.3786x-16.651です。
係数は天頂での大気吸収であり、0.38mになります。自由項(-16.7)は、吸収のない機器の大きさです。
gnuplotのチャート:
気団依存性:

高さへの依存:

厳密に言えば、良い評価を得ました。なぜなら 一般に受け入れられている平均値は0.44mです。
これにより何が得られますか?
Pogsonの式に従って、光が大気を減衰させる回数を決定します。
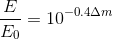
光が30%減衰することがわかります。 つまり、断面が1 m2の大気柱から塵粒子を取り出して、それらすべてを互いに近くに配置すると、それらの面積は0.3 m2になります。
清浄な(不純物を含まない)空気の吸収は0.2mであることに注意してください。 したがって、私たちの都市では、大気はきれいな空気よりも17%以上光を弱めます...
おわりに
かなり単純な分析を行い、散乱や吸収の波長依存性などの複雑なプロセスは行いませんでした。 ただし、1つの画像のみを使用してかなり正確な推定値を取得しました。 一連の画像がある場合、それらを一緒に追加すると、さらに正確な結果を得ることができます...